How to Differentiate Inverse Trig functions (AP)

Differentiating Inverse Trigonometric Functions

Inverse trigonometric functions are crucial tools in calculus for handling integrals, derivatives, and equations involving trigonometric expressions. This guide explains how to differentiate these functions step-by-step, with formulas and examples.

1. Overview of Inverse Trigonometric Functions

Inverse trigonometric functions reverse the usual trigonometric functions, returning angles from known ratios. The key inverse trig functions include:

2. Derivatives of Inverse Trigonometric Functions

The standard derivatives of these functions are derived using implicit differentiation and are as follows:

3. Using the Chain Rule

When the argument of an inverse trig function is not simply xxx, apply the chain rule:

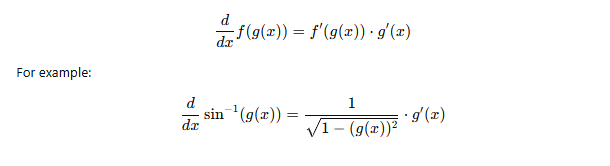
4. Examples

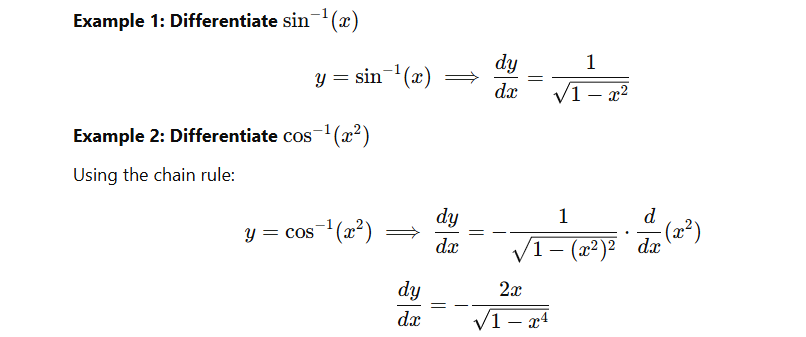
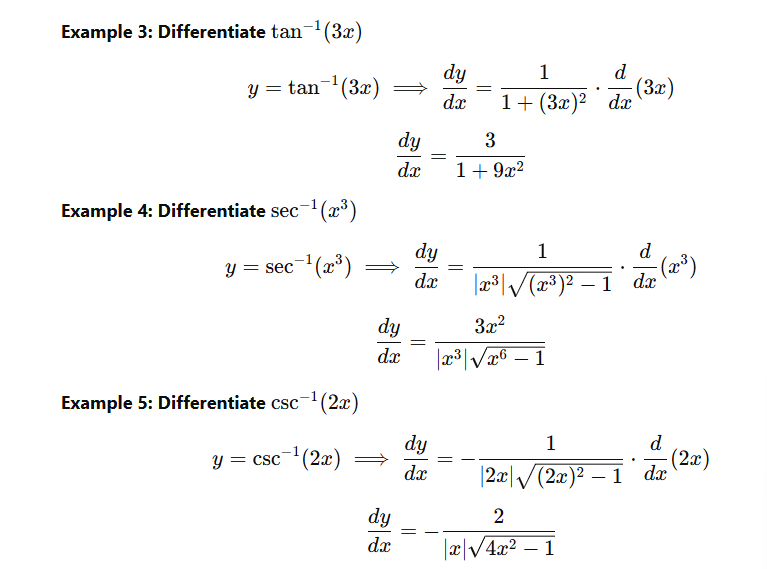
5. Key Takeaways