Riemann Sums: Everything to Know for AP Calculus

Riemann sums are a cornerstone of AP Calculus, bridging the conceptual gap between summation and integration. They provide an intuitive way to approximate areas under curves, forming the foundation for definite integrals. Let’s break it down step by step:

1. What is a Riemann Sum?

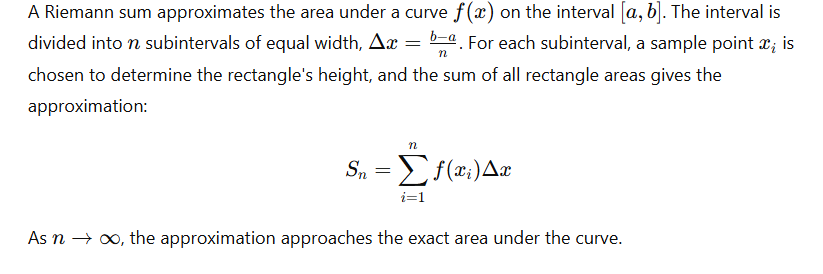
2. Types of Riemann Sums

The type of Riemann sum depends on how sample points x_i are chosen:

a. Left Riemann Sum

• Sample points: Left endpoints of subintervals.

Formula:

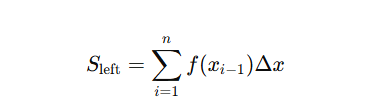
• Behavior: Underestimates if f(x) is increasing; overestimates if f(x) is decreasing.

b. Right Riemann Sum

• Sample points: Right endpoints of subintervals.

• Formula:

  

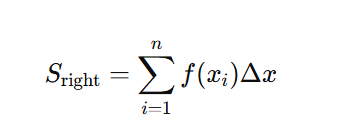
• Behavior: Overestimates if f(x) is increasing; underestimates if f(x) is decreasing.

c. Midpoint Riemann Sum

• Sample points: Midpoints of subintervals.

• Formula:

  

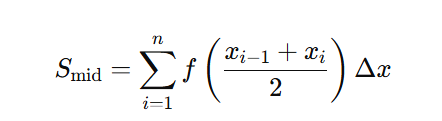
• Behavior: Typically provides a better approximation than left or right sums.

d. Trapezoidal Rule

• Approximates the curve with trapezoids.

• Formula

  

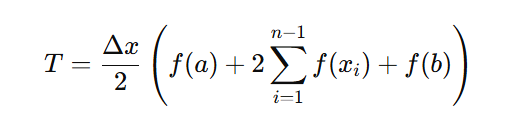
• Behavior: More accurate than the left, right, or midpoint sums.

3.Definite Integral as the Limit of Riemann Sums

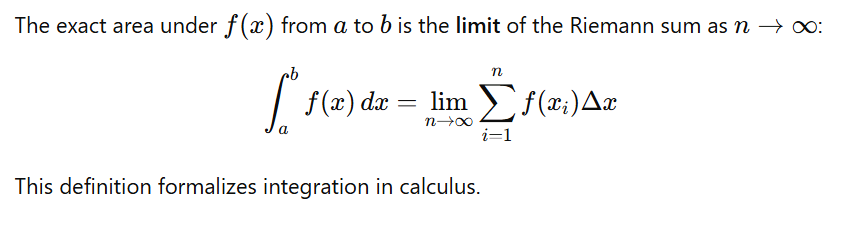
4.Understanding Riemann Sums

Factors Affecting Accuracy:

1. Number of Subintervals (n): More subintervals (n) reduce Δx, improving accuracy.

2. Choice of Sample Points: Different sample points (left, right, midpoint) affect the approximation.

3. Function Behavior: Smooth functions yield better approximations. Discontinuities or sharp changes require more subintervals for accuracy.

5.Key Concepts for AP Calculus

• Continuity: Riemann sums converge to the definite integral only if f(x) is continuous.

• Over/Underestimation:

  • Increasing function: Right sum overestimates; left sum underestimates.

  • Decreasing function: Right sum underestimates; left sum overestimates.

• Applications: Use Riemann sums to approximate real-world quantities like distance or work.

• Average Value: The average value of f(x) on [a,b]:

  

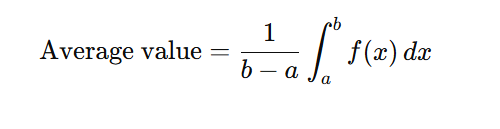
6. AP Calculus Tips

• Practice with all methods (left, right, midpoint, trapezoidal).

• Understand graphical interpretations for approximating areas.

• Be prepared to estimate integrals using Riemann sums in both tabular and algebraic forms.

• Use the trapezoidal rule for better accuracy when allowed.

7. Example Problems

8. Conclusion

Riemann sums are crucial for understanding integration. By approximating the area under curves, they pave the way for definite integrals, enabling applications in physics, engineering, and beyond. Mastery of these concepts is vital for success in AP Calculus, as well as for solving real-world problems involving accumulation and area.