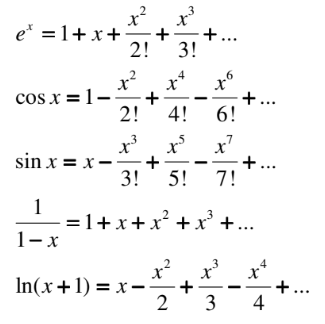AP Calculus BC Must Knows!

**L’Hopital’s Rule:**

*In plain English: if a limit results in an indeterminant form, the limit is equal to the derivative of both the numerator and denominator.*

If f(a)/g(a) = 0/0 or =∞/∞, then: lim x→a f(x)/g(x) = lim x→a f’(x)/g’(x)

\
**Average Rate of Change (slope of the secant line)**

*In plain English: The average rate of change is similar to the basic* Δy/Δx\*, but instead of y values in the numerator, there are slope values, and x values are on the bottom.\*

If the points (a, f(a)) and (b, f(b)) are on the graph of f(x) the average rate of change of f(x) on the interval \[a,b\] is: \[f(b) - f(a)\]/\[b-a\]

\
**Limit Definition of the Derivative (slope of the tangent line)**

*In plain English: If you take two points, and move them so close together you are almost (but not quite) adding 0, you create a tangent line and have therefore found the instantaneous rate of change.*

f’(x) = lim h→0 \[f(x+h) - f(x)\]/h

\
**Common derivatives YOU MUST KNOW !!!!!!!!!!**

| ==Original function== | ==Derivative== |
|----|----|
| x^n | n \* x^(n-1) |
| sin x | cos x |
| cos x | -sin x |
| tan x | (sec x)^2 |
| cot x | -(csc x)^2 |
| sec x | tan x \* sec x |
| csc x | -cot x \* csc x |
| ln x | 1/x |
| e^x | e^x |
| loga(x) | 1 / \[x \* ln a\] |
| a^x | a^x \* ln a |

\
**Properties of Log and Ln:**

ln 1 = 0

ln e^a = a

e^ln x = x

ln x^n = n ln x

ln(ab) = ln a + ln b

ln(a/b) = ln a - ln b

\
**Differentiation rules:**

**CHAIN RULE:** d/dx \[f(u)\] = f’(u) du / dx

**PRODUCT RULE:** d/dx (uv) = (u)(dv/dx) + (v)(du/dx)

**QUOTIENT RULE:** d/dx(u/v) = \[(v)(du/dx) - (u)(dv/dx)'\] / v^2

\
**Mean Value Theorem (MVT):**

*In plain English: If f(x) is made up of one going line, and there exists two y values in two coordinates (say 3 and 5), there has to be an x value where the y value is in between 3 and 5 (like 4) because the lie does not “jump” or have holes.*

If the function f(x) is continuous on \[a,b\] and the first derivative exists on the interval (a,b) then there exists a number x=c on (a,b) such that f’(c) = \[f(b)-f(a)\]/\[b-a\].

\
**Curve Sketching and Analysis:**

To find a local minimum: f’(x) changes from - to +.

To find a local maximum: f’(x) changes from + to -.

To find an absolute max/min: compile all the local points and plug back into the original function.

To find a point of inflection: f’’(x) goes from + to - or - to +.

* \
* f’’(x) is concave up
* \
* f’’(x) is concave down

\
**The Fundamental Theorem of Calculus:**

a to b∫f(x)dx = F(b) - F(a) where F’(x) = f(x)

\
**The 2nd Fundamental Theorem of Calculus:**

*In plain English: The derivative of an integral where one of the end points is a function (A) is that function plugged directly into the function in the integral (B) multiplied by the derivative of the end point function (A’)*

d/dx (# to g(x)) ∫f(x)dx = f(g(x)) \* g’(x)

\
**Average Value:**

\*\*If the function f(x) is continuous on \[a.b\] and the first derivative exists on the interval (a,b), then there exists a number x=c on (a,b) such that the average value is f(c) = 1/\[b-a\] \*\*\**∫*f(x)dx \*\*\*note the integral is from a to b

\
**Euler’s Method:** Create the table as shown. Fill out all information to find your value. Note that Δx is the “step” you are talking, and dy/dx is the slope.

| x value | y value | dy/dx | Δx | dy/dx \* Δx |
|----|----|----|----|----|

\
**Logistics Curves:**

P(t) = L / \[1+ Ce^(-Lk)t\] where L is carrying capacity.

* maximum growth rate occures when P = 1/2 L

dP/dt = kP(L - P) = (Lk)(P)(1-\[P/L\])

\
**Integrals YOU MUST KNOW !!!!!!!!!!!!!!!**

| ∫kf(u) du | k∫f(u)du |
|----|----|
| ∫du | u + C |
| ∫1/\[(1-x^2)^1/2\] dx | inverse sin |
| ∫ -1/\[1-x^2)^1/2\] dx | inverse cos |
| ∫1/(1+x^2) dx | inverse tan |
| ∫-1/(1+x^2) | inverse cot |
| ∫1/\[\|x\|(x^2-1)^1/2\] | inverse sec |
| ∫-1/\[\|x\|(x^2-1)^1/2\] | inverse csc |

\
**Integration by Parts:**

∫u dv = uv - ∫v du

USE LIPET TO DETERMINE U:

* Logs
* Inverse trig
* Polynomial functions
* Exponential functions
* Trig

\
**Arc Length:**

For a function f(x): L = ∫\[(1+f’(x)^2\]^1/2 dx

For a polar graph r(θ): L = \[(r(θ)^2+(r’(θ)^2\]^1/2 dθ

\
**Lagrange Error Bound:**


**Distance, velocity, acceleration**

Velocity = d/dt (position)

Acceleration = d/dt (velocity)

Velocity vector =

Speed = |v(t)| = \[(x’)^2+(y’)^2\]^1/2