Princeton Review AP Calculus BC, Chapter 8: Integration & Accumulation of Change
The Integral & Area Under A Curve
Up to here we’ve learned about the derivative, the rate of change. Now we have the integral ∫ also called the antiderivative.
- The derivative shows us the change/unit
- So the antiderivative shows us the total change
The first type is called a definite integral and shows us the area of the region under the function and the x-axis. It gives us the accumulation/total change!
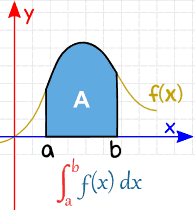
Let’s say we have a function that is shaped like that (or any function at all), if the definite integral needs us to get the area under the function, how would we do that?
- Because this is a shape that we have no formula for, we can estimate it using shapes that we do know
- We can split this area up into rectangles!
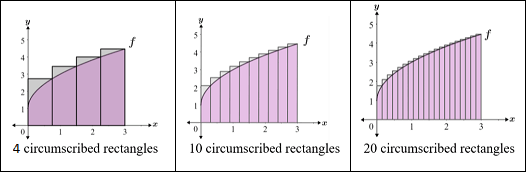
The more rectangles we have, the better our estimate is!
- This method is called a Riemann sum!
Riemann & Trapezoidal Sums
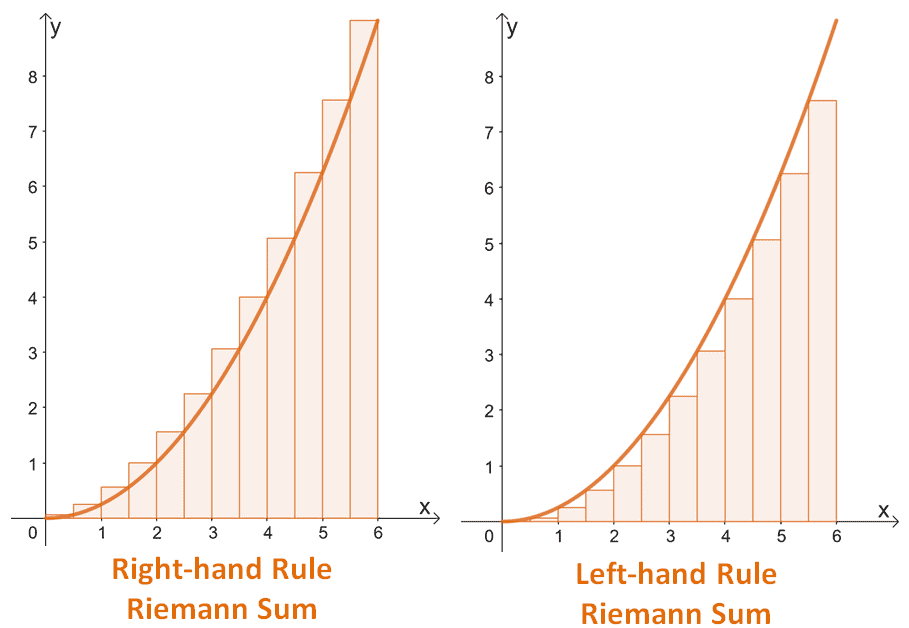
We can take a Riemann Sum from the left, or from the right!
- For left-handed sums we use the endpoints (number) on the left
- For right-handed sums we use the endpoints (number) on the right!
The formulas are the same for any rectangle, base * height!
Take the width of your rectangle and multiply it by the height of the rectangle!
Do this for each rectangle you have and add them all together
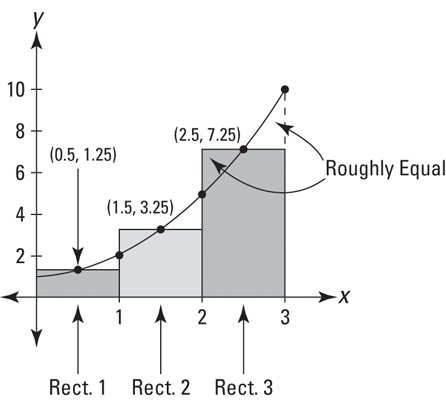
To get these rectangles even more accurate, we can use a midpoint sum
- We still use the formula for a rectangle, but we use the value for the height in between!
A shape that would more closely fit the shape of the curve is a trapezoid
Therefore, we can use trapezoidal sums!
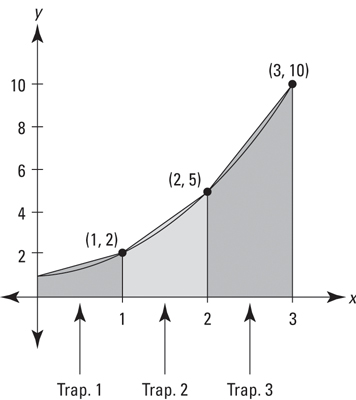
We know that the formula for a trapezoid is (1/2)(b1 + b2)(h)
- For example, our second trapezoid would be (1/2)(2 + 5)(1)
- Still a width of 1 but we add the two heights!
Most of the time you are given a table to take a Riemann Sum from!
| 0 | 2 | 4 | 7 |
|---|---|---|---|
| 1 | 6 | 10 | 15 |
- Left Sum: (2)(1) + (2)(6) + (3)(10)
- Notice how this is a left sum so we don’t use the furthest right value
- Right Sum: (2)(6) + (2)(10) + (3)(15)
- Same thing for the right, except we don’t use the furthest left value
- Midpoint: (4)(6)
- Not complete but you see how we use a width of 4 and then the height in between
- Trapezoid: (1/2)(1+6)(2) + (1/2)(6+10)(2) + (1/2)(10+15)(3)
Tabular Riemann Sums
- The majority of the time when you have to use a Riemann Sum, the AP gives it to you in tabular format
| Years:(t) | 2 | 3 | 5 | 7 | 10 |
|---|---|---|---|---|---|
| Height:H(t) | 1.5 | 2 | 6 | 11 | 15 |
- Trapezoids: (1/2)(1.5+2)(1) + (1/2)(2+6)(2) + (1/2)(6+11)(2) + (1/2)(11+15)(3)
- Left Sum: (1)(1.5) + (2)(2) + (2)(6) + (3)(11)
- Right Sum: (1)(2) + (2)(6) + (2)(11) + (3)(15)
- You do not have to simplify these!
Fundamental Theorem of Calculus & Antiderivatives
For differentials, you know that you had a set of different rules that you can use to take the derivative. The same applies for the antiderivative!
- Intuitively, it’s the opposite of what you do to take a derivative EXCEPT…
- We can only use the power rule!
- If the power rule for a derivative tells us to multiply down and decrease the power, then the opposite of that would be to divide and increase the power!
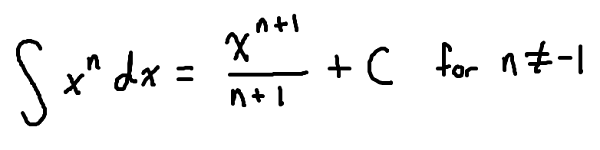
The +C is very important!
- If you take the derivative of any number without an x, you get zero
- Therefore if we’re doing the reverse process, we don’t know what this number could be, therefore we add on a C for the constant of integration
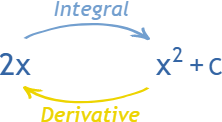
The integral of 2x is really 2x^2/2 but that simplifies to x^2!
Remember that if the integral is not in power rule format, we must algebraically manipulate it so that we can use the power rule

The two numbers at the top and bottom of the integral means that it is a definite or bounded integral
It means we are trying to find the area below 2 and 3
Because we have a function, we don’t have to graph it out, instead we have something called the First Fundamental Theorem of Calculus
- (8 chapters in and you’re just now learning about the thing fundamental to calculus huh)
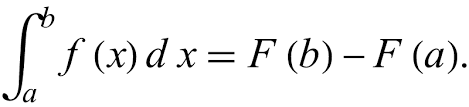 The first fundamental theorem says that the integral from a to b is equal to the antiderivative, plug in b, and then plug in a and subtract!
The first fundamental theorem says that the integral from a to b is equal to the antiderivative, plug in b, and then plug in a and subtract!Let’s say that we had ∫2x from before (from x=2 to x=3), according to the first fundamental theorem it is equal to (3)^2 - (2)^2
Advanced Integration
Sometimes, getting an integral into power rule format is nearly impossible, in those cases there are other techniques we can do!

If your integral contains trigonometry, the best thing to do is just memorize the derivative of trig functions, and the integral will be the opposite
- Ex. d/dx sinx = cosx
- Therefore, ∫cosx = sinx
You can manually derive these but because this is a timed AP exam it’s more efficient to memorize these!
Your other option is U-substitution!

- Chose a term to be your “u”
- Take the derivative of this value to get du/dx
- Substitute in your u value for the term and your du/dx value for dx
- Take the integral
- U-substitution is tricky but helpful for some problems!
- You got this!!! 👍
- Ex. ∫(x - 4)^10
- Let u = x-4
- du/dx = 1
- dx = du/1
- ∫(u)^10 du
- u^11/11 + C
- (x-4)^11/11 + C