Simple Harmonic Motion Examples to Know for AP Physics 1 (2025)
Simple harmonic motion (SHM) is a type of periodic motion in which the restoring force acting on an object is directly proportional to its displacement from the equilibrium position. This concept is integral in understanding various physical systems and their oscillatory behavior, as outlined below.
Simple Pendulum
A simple pendulum consists of a mass (bob) attached to a string or rod of fixed length.
The motion is periodic, and its period T is given by:
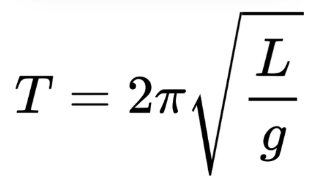
where:
L: Length of the pendulum,
g: Acceleration due to gravity.
The restoring force is the component of gravitational force that acts to bring the bob back toward the equilibrium position.
The motion closely approximates SHM when the angular displacement is small (<15∘). At larger angles, the approximation breaks down due to nonlinearities.
Mass-Spring System
This system involves a mass attached to a spring, which oscillates when displaced from equilibrium.
The period of oscillation is described by:
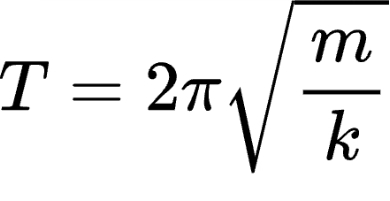
Where:
m: Mass of the object,
k: Spring constant (a measure of stiffness).
The restoring force follows Hooke’s Law:
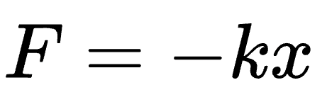
Where:
x is the displacement from equilibrium.
Energy in the system oscillates between:
Potential energy stored in the spring,
Kinetic energy of the moving mass.
Torsional Pendulum
A torsional pendulum consists of a mass suspended by a wire or rod that twists about its axis when displaced.
Its period of oscillation is determined by:
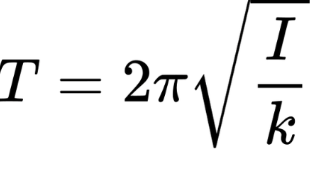
Where:
I: Moment of inertia of the system.
κ: Torsional constant of the wire or rod.
The restoring torque, similar to linear SHM systems, is proportional to the angle of twist.
Torsional pendulums are commonly used in material property analysis.
Vibrating String (e.g., Guitar String)
A string fixed at both ends vibrates to produce sound. The vibration creates standing waves with:
Nodes: Points of zero displacement,
Antinodes: Points of maximum displacement.
The string's fundamental frequency depends on:
The string’s length,
The tension (T) applied to the string,
The mass per unit length (μ).
The wave speed is given by:
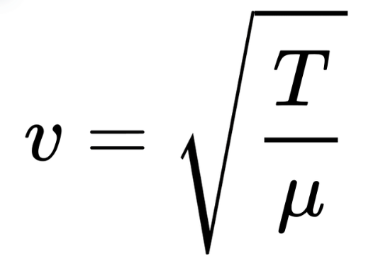
Where:
T: Tension in the string
μ: Mass per unit length of the string.
The fundamental frequency is determined by the length, tension, and mass of the string. Higher harmonics (integer multiples of the fundamental frequency) create a complex sound spectrum, enriching the tone of the instrument.
Oscillating Liquid in a U-Tube
When liquid in a U-tube is displaced from its equilibrium level, it oscillates due to gravity.
The period of oscillation is approximately:
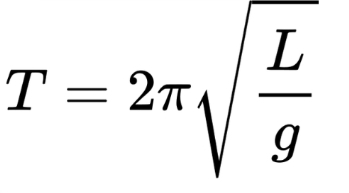
Where:
L: Effective length of the liquid column,
g: Acceleration due to gravity.
The restoring force is generated by the difference in height between the liquid columns, pulling the system back to equilibrium.
Vibrating Tuning Fork
A tuning fork, when struck, vibrates at a specific frequency, creating sound waves through the surrounding air.
The frequency depends on the material, dimensions, and shape of the fork.
The prongs of the tuning fork exhibit SHM, with their motion creating consistent sound waves.
Tuning forks are widely used for musical tuning and in experimental physics due to their precise and stable frequency.
Oscillating Electrical Circuit (LC Circuit)
An LC circuit comprises an inductor (L) and a capacitor (C), which exchange energy between magnetic and electric fields.
The natural frequency of oscillation is given by:
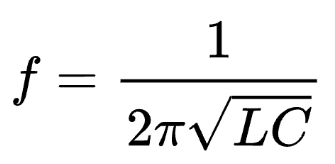
The oscillations are analogous to mechanical SHM, where energy transitions between potential (electric) and kinetic (magnetic) forms.
Resistance in the circuit can cause damping, reducing the amplitude of oscillations over time.
Mass-Spring Systems
a. Vertical Mass-Spring System
A mass hanging from a spring oscillates vertically when displaced.
The equilibrium position shifts due to the weight of the mass, but the period remains:
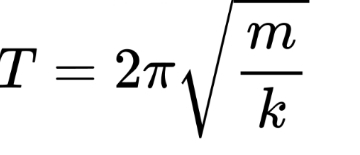
b. Horizontal Mass-Spring System
On a frictionless surface, a mass attached to a spring oscillates purely horizontally.
The absence of gravity’s influence simplifies the system, and the period is the same as the vertical system.
Bungee Jumping
A bungee jumper experiences oscillatory motion due to the interplay of:
Gravitational force pulling them downward,
Elastic force from the stretched bungee cord pulling them upward.
The motion is complex, with the period varying as the cord stretches and contracts. This real-world example highlights SHM principles applied in dynamic, non-ideal systems.
Applications and Insights
SHM underpins numerous applications, including musical instruments, engineering designs, and scientific measurements. By understanding the relationships between forces, energy transformations, and system parameters, we can analyze and predict oscillatory behaviors in a wide range of contexts. From precision timekeeping to wave propagation, SHM connects theoretical physics with practical innovation.
 Knowt
Knowt
