Electric Charge:

• In an isolated system, charge is always conserved.

• Protons and electrons have a quality called electric charge.

• Charge is invariant in nature (value of charge doesn’t depend on frame of reference).

• Charge is quantised (it means any charge on the body is an integral multiple of the fundamental amount of electric charge).

  • Q = n e

  • e = 1.6 * 10^-19 C

Coulomb’s Law:

The electric force between two charged particles obeys a law that is very similar to the gravitational force between two masses. So, called inverse square laws.

• Electric force between two particles with charges q1 and q2, separated by distance r, has a magnitude by the equation:

  

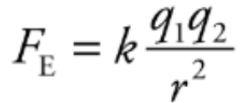
• The value of the proportionality constant k, depends on the material between the charged particles. Generally, called a Coulomb’s constant.

  • k0 = 9 * 10^9 N. m^2/C^2 written as,

    

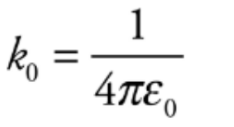
  • e0 is known as the permittivity of free space.

• Example: A dipole is formed by two point charges, each of magnitude 4.0 nC, separated by a distance of 6.0 cm. What is the strength of the electric field at the point midway between them?

• Solution. Let the two source charges be denoted +Q and -Q. At Point P, the electric field vector due to +Q would point directly away from +Q, and the electric field vector due to -Q would point directly towards -Q. Therefore, these two vectors point in the same direction (from +Q to -Q), so their magnitudes would add.

  

  Using the equation for the electric field strength due to a single point charge, we find that

  

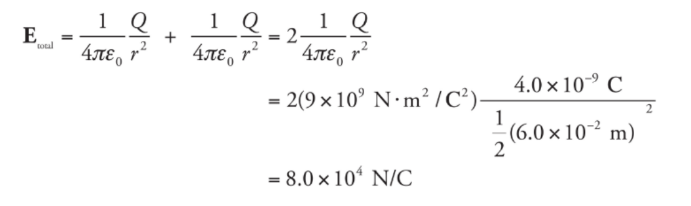
• Example: Consider the proton and electron in hydrogen. The proton has a mass of 1.6 × 10−27 kg and a charge of +e. The electron has a mass of 9.1 ×10−31 kg and a charge of −e. In hydrogen, they are separated by a Bohr radius, about 0.5 × 10−10 m. What is the electric force between the proton and electron in hydrogen? What about the gravitational force between the proton and electron?

• Solution. The electric force between the proton and the electron is given by Coulomb’s Law:

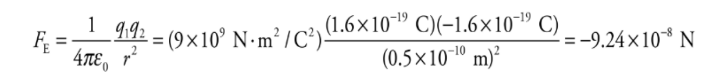
The fact that FE is negative means that the force is one of attraction, which we naturally expect, since one charge is positive and the other is negative. The force between the proton and electron is along the line that joins the charges, as we’ve illustrated below. The two forces shown form an action/reaction pair.

Now, the gravitational force between the two charges is given by Newton’s Law of Gravitation:

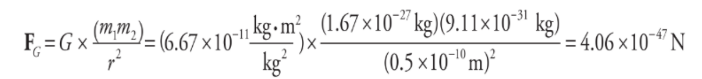
Now, compare the orders of magnitude of the electric force to the gravitational force. The electric force has an order of magnitude of 10^-8 N, but the gravitational force has an order of magnitude of 10^-47 N! This means that the electric force is something like 10³9 times larger! This is the reason that in problems where we calculate electrostatic forces, we often neglect gravitational forces.

Addition of forces:

• Consider three point charges: q1, q2, and q3. The total electric force acting on, say, is simply the sum of F1-on-2, the electric force on q2 due to q1, and F3-on-2, the electric force on q2 due to q3:

  

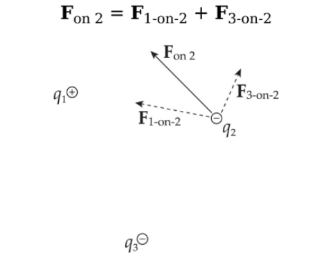
• Example: Consider four equal, positive point charges that are situated at the vertices of a square. Find the net electric force on a negative point charge placed at the square’s center.

• Solution: Refer to the diagram below. The attractive forces due to the two charges on each diagonal cancel out: F1 + F3 = 0, and F2 + F4 = 0, because the distances between the negative charge and the positive charges are all the same and the positive charges are all equivalent. Therefore, by symmetry, the net force on the center charge is zero.

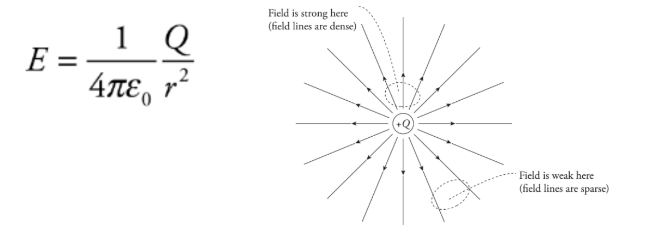
Electric Field:

• The space is surrounded by a charge in which another charged particle experiences the force.

• The electric field vector E:

  

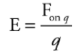
• The strength of the electric field created by a point-charge source of magnitude Q. This is the electric field surrounding a point charge.

• Example: A charge q = +3.0 nC is placed at a location at which the electric field strength is 400 N/C. Find the force felt by the charge q.

• Solution. From the definition of the electric field, we have the following equation:

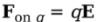  Therefore, in this case, F on q = qE = ( 3× 10^-9 C)(400 N/C) = 1.2 × 10^-6 N.

• There are three types of electric fields:

  • Radial field: this occurs from a point charge/ charged sphere.

    • These fields are inversely proportional to the square of the distance from the point charge.

  • The second type of field is generated by a collection of point charges with specified locations and charges:

    • Here, the results in an electric field are determined by superposition.

  • The third type of field is an infinite sheet of charge:

    • It is constant in both magnitude and direction.

• The electric fields follow same properties as the electric force.

• The electric field lines never cross.

• Electric field lines always point away from positive source charges and toward negative ones. The pair is called an electric dipole.

• Electric field is always perpendicular to the surface, no matter what shape the surface may be.

The Uniform Electric Field:

• A lot of problems deal with uniform electric fields.

• The field may be taken as uniform at least in the middle.

• Uniform field just signifies the constant force.

• Example: Positive charge is distributed uniformly over a large, horizontal plate, which then acts as the source of a vertical electric field. An object of mass 5 g is placed at a distance of 2 cm above the plate. If the strength of the electric field at this location is 106 N/C, how much charge would the object need to have in order for the electrical repulsion to balance the gravitational pull?

Solution. Clearly, since the plate is positively charged, the object would also have to carry a positive charge so that the electric force would be repulsive.

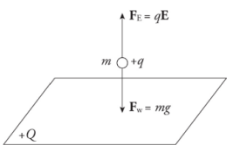Let q be the charge on the object. Then, in order for Fe to balance mg, we must have

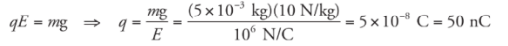
Conductors and Insulators:

• Conductors: Materials that generally allow the flow of excess charge without resisting it.

  • Metals, aqueous solutions, etc.

• Insulators: Materials which resist the flow of electrons.

  • Glass, rubber, wood, and plastic.

Methods of Charging:

• Through charging by friction:

  • It involves rubbing the insulator against another material, thereby stripping electrons from one to another material.

• Through conduction:

  • When we connect two conductors charge flows from one to another until the potential of both the conductors becomes the same.

  

• Through induction: The process of charging by induction may be used to redistribute charges among a pair of neutrally charged spheres.

  • In the end, both spheres are charged.

  • Let’s imagine two neutrally charged spheres that are set on an insulating stand. They are in contact with each other.

    
    

  • When a charge is brought near one of the spheres then, excess negative charges are located on the right sphere and positive excess charges are at the left sphere.

    

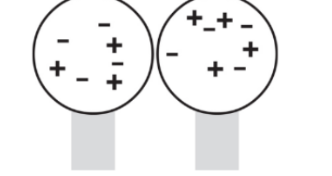
  • When the external charge is still nearby, the two conducting spheres are separated. Because the conductors are no longer in contact, the negative charge has been trapped on the right sphere and the positive charge has been trapped on the left sphere.

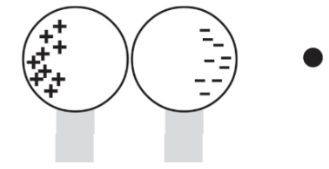
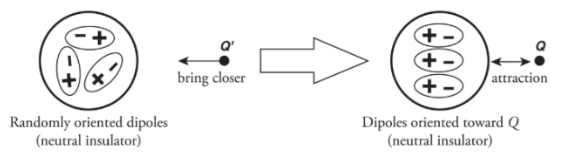
    Note: the net charge is unchanged but, the distribution of charges is changed.

  • If the sphere was made up of glass (an insulator):

    • There aren’t any free electrons.

    • The atoms that make up the sphere will become polarised.

      

Electrical Potential Energy:

• WE is the work done by the electric force, then the change in the charge’s electrical potential energy is defined by:

  

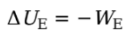
• Example: A positive charge +q moves from position A to position B in a uniform electric field E: What is its change in electrical potential energy?

• Solution. Since the field is uniform, the electric force that the charge feels, FE = qE, is constant. Since q is positive, FE points in the same direction as E, and, as the figure shows, they point in the same direction as the displacement, r. This makes the work done by the electric field equal to We = FEr = qEr, so the change in the electrical potential energy is

  

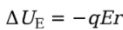
  Note that the change in potential energy is negative, which means that potential energy has decreased; this always happens when the field does positive work. It’s just like dropping a rock to the ground: Gravity does positive work, and the rock loses gravitational potential energy.

Electrical Potential Energy from a Point Charge:

• Electrical potential energy required to move along the field lines surrounding a point charge is given by:

  

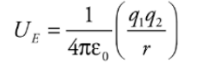
• Example: A positive charge q1= +2 × 10−6 C is held stationary, while a negative charge, q2 = −1 × 10−8 C, is released from rest at a distance of 10cm from q1. Find the kinetic energy of charge q2 when it’s 1 cm from q1.

• Solution. The gain in kinetic energy is equal to the loss in potential energy; you know this from the Conservation of Energy. Previously, we looked at constant electric fields and were able to use the equation for work from a constant force. However, when the field (and therefore the force) changes, we need another equation. Electrical potential energy required to move along the field lines surrounding a point charge is given by:

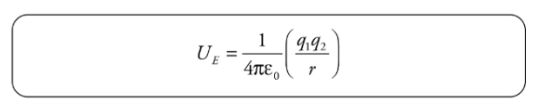  Therefore, if q1 is fixed and q2 moves from rA to rB, the change in potential energy is

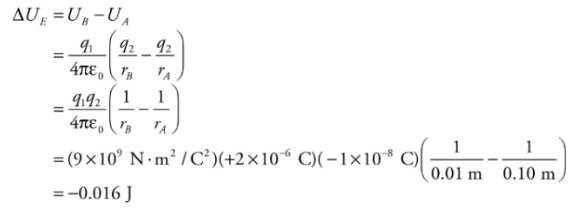  Since q2 lost 0.016 J of potential energy, the gain in kinetic energy is 0.016 J. Since q2 started from rest (with no kinetic energy), this is the kinetic energy of q2 when it’s 1cm from q1.

Electric Potential:

It is a scalar property of every point in the region of the electric field. At a point in the electric field potential is defined as the interaction of a unit positive charge. If at a point in the electric field, a charge q has potential energy U, then the electric potential at that point can be given as

Electric potential is electrical potential energy per unit charge, and the units of electric potential are joules per coulomb.

Electrical Potential Energy from a Point Charge:

• Consider the electric field created by a point source charge Q. If a charge q moves from a distance rA to a distance rB from Q, then the change in the potential energy is:

  

• The difference in the electric field between positions A and B in the field created by Q is:

  

• If Va tends to zero and ra tends to infinity, then for a point charge Q, the electric potential at a distance r from Q is:

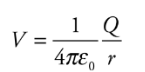  Note: Electric Potential and Electric Potential Energy, although very closely related and have similar names, are not the same thing. Even the units are measured differently—the electric potential is measured in joules per coulomb and the electric potential energy is in joules.

• Example: Let Q = 2 × 10−9 C. What is the potential at a Point P that is 2 cm from Q?

• Solution. Relative to V = 0 at infinity, we have

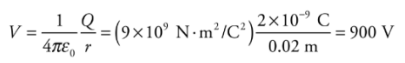
Equipotential surfaces:

• They are the surfaces of constant potential.

• The equipotentials are always perpendicular to the electric field lines.

Addition of Electric Potential:

• The formula V = kQ/r helps us to find the potential due to a single point source charge, Q.

• Potential is scalar.

• So, when adding up the potential it is simply adding numbers and nothing complicated like adding up the vectors.

• When calculating the change in potential energy, the change in positions should be kept in mind.

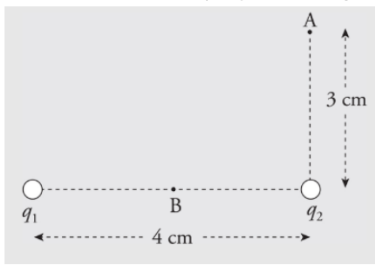
• Example: How much work would it take to move a charge q = +1 × 10−2 C from Point A to Point B (the point midway between q1 and q2)?

• Solution.

  ΔUΕ = qΔV, so if we calculate the potential difference between Points A and Band multiply by q, we will have found the change in the electrical potential energy. Then, since the work by the electric field is −ΔU, the work required by an external agent is ΔU. First, we need the potential at point A, VA. Since there are two charges q1 and q2 contributing to the potential at point A, we calculate the contribution of each using and sum the results. Remember that the potential is a scalar quantity and so no vector addition is required here. It is very important to keep track of the positive and negative signs, however.

A similar calculation can be carried out for point B, although the distance from the charges will be different for point B than they were for point A.

Δ VA → B = VB - VA = (-900 V) - (-1080 V) = +180 V. This means that the change in electrical potential as q moves from A to B is

This is the work required by an external agent to move q from A to B.

Equipotential Curves and Equipotential Maps:

• Equipotential Curve: Equipotential curves are curves of constant elevation. If you walk along any of the contour lines and you neither ascend or descend, then the curve is known as the equipotential curve.

• Equipotential Map: A drawing of several equipotential curves at various values of the potential for a charge distribution is called an equipotential map.

• Both equipotential maps are made of concentric circles.

• Everywhere, the equipotential curves meet the field lines, and the two curves meet at a right angle.

• The equipotential map for an isolated positive charge is exactly the same as that for an isolated negative charge.

The equipotential map and some electric field lines for an electric dipole

• The electric field is strong where the field lines which are solid here are densely packed and weak where they are spread out.

• The equipotential map shows lines at a constant voltage difference ΔV, so the field strength, is strong when the distance, r, between the lines is small.

The Electric Potential of a uniform field:

• Example: Consider a very large, flat plate that contains a uniform surface charge density σ. At points that are not too far from the plate, the electric field is uniform and given by the equation:

  What is the potential at a point which is a distance d from the sheet (close to the plates), relative to the potential of the sheet itself?

• Solution. Let A be a point on the plate and let B be a point a distance d from the sheet. Then

  Since the field is constant, the force that a charge q would feel is also constant, and is equal to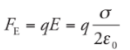

  Therefore,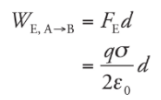

  

  so applying the definition gives us

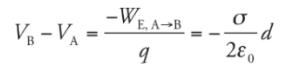  This says that the potential decreases linearly as we move away from the plate.

• Example: Two large flat plates—one carrying a charge of + Q, the other −Q—are separated by a distance d. The electric field between the plates, E, is uniform. Determine the potential difference between the plates.

• Solution. Imagine a positive charge q moving from the positive plate to the negative plate:

  

  Since the work done by the electric field is

  the potential difference between the plates is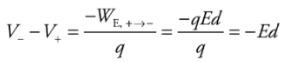

  This tells us that the potential of the positive plate is greater than the potential of the negative plate, by the amount Ed. This equation can also be written as

  Therefore, if the potential difference and the distance between the plates are known, then the magnitude of the electric field can be determined quickly. The magnitude is simply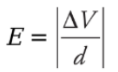

  

  ---

  Capacitors and Capacitance:

• Capacitor: Two conductors, separated by some distance that carry equal but opposite charges +Q and -Q. The pair comprises a system called a capacitor.

• Parallel-Plate capacitor: The capacitor is in the form of parallel metal plates or sheets.

• Therefore, with two plates, one with surface charge density +σ, and the other−σ, the electric combines to give a field that’s zero outside the plates and that has magnitude

  

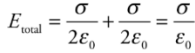
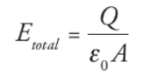
• Capacitance: Q is the total charge stored on either plate of a capacitor, and ΔV is the potential difference between the plates. The ratio of Q to ΔV, for any capacitance, is defined as its capacitance.

• C = Q/ΔV

• The capacitance measures the capacity for holding charge.

• For a parallel-plate capacitor we get:

  

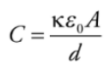
Electric Field and Capacitors:

• The electric field E always points from the positive plate towards the negative plate, and the magnitude remains the same at every point between the plates.

• Uniform electric is approximately true because the electric field is constant everywhere only in an infinitely large sheet of charge which is quite impossible to construct.

• ΔV = Ed

Fringing Fields:

• The plates of the capacitor are infinitely large.

• Analysis is good near the center of the plates than the edges.

• For areas beyond the edges, we approximate the field as the sum of the capacitor field and a dipole formed by the charges at the edges of the p

Energy stored in Capacitor:

• Example: A 10-nanofarad parallel-plate capacitor holds a charge of magnitude 50 μC on each plate. (a) What is the potential difference between the plates? (b) If the plates are separated by a distance of 0.2 mm, what is the area of each plate?

• Solution

  a) From the definition, C = Q/ΔV, we find that

  

  b) Because K = 1, we have the equation C = ε0A/d, and can calculate the area, A, of each plate:

  

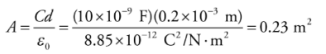
Capacitors and dielectric:

• To keep the plates of the capacitor apart they are filled with dielectric which increases the capacitance of the capacitor.

  

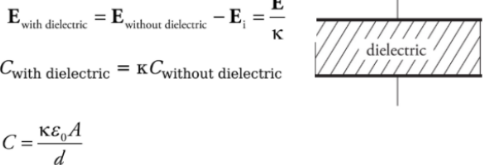
  Note: Why can’t we use a conductor?

  If a conductor is placed between the plates, the charges are no longer separated and the device is no longer a capacitor.