The Nth Term Test for Divergence is a straightforward and essential tool in the study of infinite series. This test examines the behavior of the general term ana_nan​ as n→∞n \to \inftyn→∞, helping to determine whether a series diverges.

Understanding Infinite Series

An infinite series is written as:

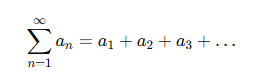
Here:

• a_n is the n-th term of the series.

• The series can either:

  • Converge (approach a finite value), or

  • Diverge (grow indefinitely or oscillate).

The Nth Term Test for Divergence helps identify if a series definitely does not converge.

Why the Test Works

For a series to converge, the individual terms ana_nan​ must get smaller and smaller, approaching zero as n→∞.

• If a_n does not approach zero, the sum cannot settle to a finite value, and the series diverges.

However, the reverse is not true: lim_n→∞​an​=0 is a necessary condition for convergence but not sufficient. This limitation highlights why the Nth Term Test only shows divergence.

Steps to Apply the Nth Term Test

1. Identify the General Term
   Write the explicit formula for a_n.

2. Compute the Limit
   Find lim_n→∞​a_n using limit laws, simplifications, or algebraic techniques.

3. Analyze the Result

   • If the limit is not zero (≠0) or does not exist, the series diverges.

   • If the limit is zero, the test is inconclusive; use other tests (e.g., Comparison Test, Ratio Test) to check convergence.

Special Considerations

• Oscillatory Terms:
  If an oscillates (e.g., a_n=(−1)ⁿ, the limit may not exist, leading to divergence.

• Slowly Decreasing Terms:
  Even if lim⁡_n→∞a_n=0​, the series may diverge.

Conclusion

The Nth Term Test for Divergence is a simple but powerful tool for determining whether an infinite series diverges. While it cannot confirm convergence, its application as a first step in series analysis provides essential insights. Understanding its strengths and limitations ensures accurate results and guides the use of more advanced tests when necessary.