Gas Laws Overview

• Purpose: Describe the relationships between pressure (P), volume (V), temperature (T), and number of moles (n) in gases.

• Real-World Applications: Explains phenomena such as weather patterns, breathing mechanics, car engines, and chemical reactions.

• Key Assumptions for Ideal Gases:

  • Gas particles have negligible volume compared to the container.

  • No interactions (attractions or repulsions) between gas molecules.

  • Collisions between gas molecules and container walls are perfectly elastic.

  • Temperature is directly proportional to the average kinetic energy of gas particles.

Key Gas Law Equations

1. Ideal Gas Law :

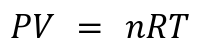
• Key Variables:

  • P: Pressure (in Pascals or atm)

  • V: Volume (in liters or m³)

  • n: Number of moles of gas

  • R: Universal Gas Constant (8.31 J/(mol·K) or 0.0821 L·atm/(mol·K))

  • T: Temperature (K=°C+273.15)

• Description:

  • Describes the relationship between pressure, volume, temperature, and the amount of gas.

  • Assumes the gas is "ideal" (no intermolecular forces and negligible molecular size).

• Applications:

  • Calculating missing gas properties (e.g., pressure, volume, etc.).

  • Understanding behaviors in sealed containers (e.g., inflating balloons).

• Example Problem:

• A gas occupies 10 L at 2 atm and 300 K. Find the number of moles (n).

• Solution:

  

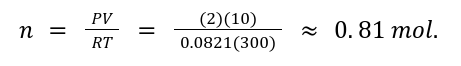
2. Boyle's Law:  

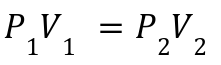
• Explanation:

  • Pressure and volume are inversely proportional if temperature remains constant.

  • When the volume increases, pressure decreases, and vice versa.

• Applications:

• Compression and expansion of gases in closed systems.

• Scuba diving: Pressure changes as depth increases or decreases.

• Key Concept:

  • Works only at a constant temperature.

• Example Problem:

• A gas has P₁ = 1 atm, V₁ = 4L. If compressed to 2 L, what is P_2​?

• Solution: 

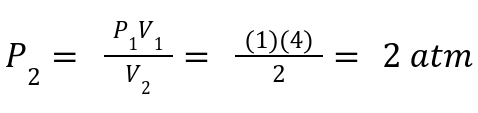
3. Charles's Law:

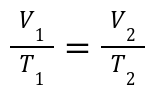
• Explanation:

  • Volume and temperature are directly proportional at constant pressure.

  • Gas expands when heated and contracts when cooled.

• Applications:

  • Behavior of hot air balloons (hot air expands, increasing volume).

  • Design of thermal engines and heating systems.

• Key Concept:

  • Temperature must be in Kelvin.

• Example Problem:

  • A gas has V₁ = 3L , T₁ = 300 K. If heated to 600 K, what is V₂?

  • Solution:

    

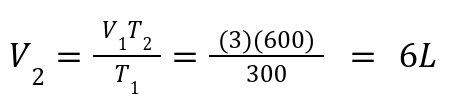
4. Gay-Lussac's Law:

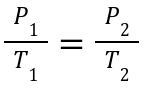
• Explanation:

  • Pressure and temperature are directly proportional at constant volume.

  • Heating a gas increases its pressure.

• Applications:

  • Pressure cookers: Gas pressure increases as the temperature rises.

  • Understanding pressurized gas systems (aerosol cans, propane tanks).

• Example Problem:

  • A gas has P_1​ = 2atm, T₁= 300 K .If heated to T₂= 450 K, what is P₂​?

  • Solution:

    

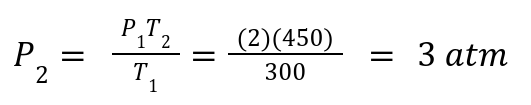
5. Combined Gas Law:

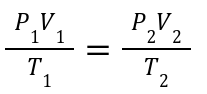
• Combines: Boyle’s, Charles’s, and Gay-Lussac’s laws.

• Useful When: Pressure, volume, and temperature all change, but the number of moles remains constant.

• Applications:

  • Predicting gas behavior in changing environmental conditions.

  • Solving problems involving gas systems with multiple variables.

6. Avogadro's Law:

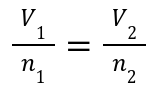
• Relationship: Volume is directly proportional to the number of gas moles at constant temperature and pressure.

  • Doubling the amount of gas (moles) doubles the volume.

• Applications:

  • Stoichiometry in chemical reactions involving gases.

  • Behavior of gas mixtures in containers.

7. Dalton's Law of Partial Pressures: 

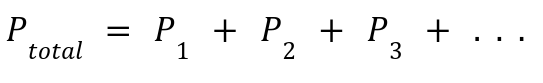
• Definition: The total pressure of a gas mixture equals the sum of the partial pressures of each gas.

  • P_i​ : Pressure each gas would exert if it alone occupied the container.

• Applications:

  • Explains respiratory processes (e.g., oxygen and carbon dioxide in lungs).

  • Used in calculating gas behavior in chemical reactions and diving systems.

8. Kinetic Theory of Gases: 

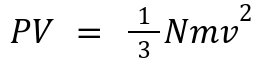
• Relates:

  • P and V: Macroscopic properties.

  • N, m, and v: Microscopic behavior (number, mass, and velocity of particles).

• Key Insight:

  • Pressure arises from collisions of gas molecules with container walls.

  • Temperature is proportional to average kinetic energy: 

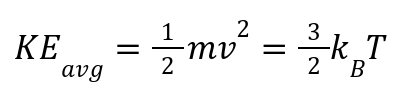
•  where k_B = 1.38 X 10^-23 J/K (Boltzmann constant).

• Applications:

  • Explains molecular motion and diffusion rates.

  • Basis for understanding gas pressure and temperature relationships.

9. Root Mean Square Speed: 

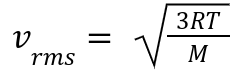
• Definition: Calculates the average speed of gas molecules:

  • R: Gas constant.

  • T: Temperature in Kelvin.

  • M: Molar mass (kg/mol).

• Key Insight:

  • Higher temperature → faster molecular motion.

  • Lighter molecules move faster than heavier ones at the same temperature.

• Applications:

  • Explains gas diffusion and effusion (e.g., Graham's law).

10. Molar Mass from Density: 

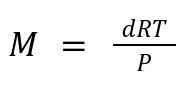
• Relates: Gas density (d) to molar mass (M), temperature (T), and pressure (P).

• Applications:

  • Identifying unknown gases based on experimental data.

  • Calculating molar masses in gas reactions or mixtures.

Applications of Gas Laws in Real Life

1. Breathing Mechanics:

   • Boyle’s Law explains how lungs expand (decreasing pressure) to draw in air.

2. Hot Air Balloons:

   • Charles’s Law describes the thermal expansion of air as it is heated, increasing volume and causing lift.

3. Respiration and Gas Mixtures:

   • Dalton’s Law explains how oxygen and carbon dioxide exchange occurs in the lungs.

4. Weather Patterns:

   • Ideal Gas Law explains changes in atmospheric pressure with temperature variations.

5. Diving and Decompression:

   • Dalton’s and Henry’s Laws help divers avoid decompression sickness by understanding gas solubility under pressure.

6. Engines and Combustion:

   • Combined Gas Law explains the behavior of gases during compression and expansion cycles.