Riemann Sums is a fundamental concept in calculus used to approximate the area under a curve. They form the basis for understanding definite integrals and are a crucial topic in AP Calculus. Here's everything you need to know about Riemann Sums.

1. What is a Riemann Sum?

A Riemann Sum is an approximation of the integral of a function over an interval [a,b] by dividing the interval into smaller subintervals and summing up the areas of rectangles.

2. Types of Riemann Sums

The type of Riemann Sum depends on how the heights of the rectangles are determined:

3. Components

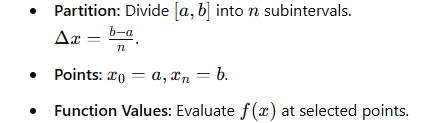
4. Calculation Steps:

• Identify [a,b] and n.

• Compute Δx.

• Choose a Riemann Sum type.

Evaluate f(x) and calculate the sum.

5.Example:

6. Connection to Integrals:

7. Tips for Success

1. Understand the geometry:

   • Visualize how rectangles (or trapezoids) approximate the curve.

2. Practice with different sums:

   • Get comfortable with left, right, midpoint, and trapezoidal methods.

3. Connect with integrals:

   • See how Riemann Sums transitions into definite integrals.

4. Calculator Skills:

   • Use calculator programs to evaluate sums for larger n.

8. AP Calculus Applications

• Approximation techniques in free-response questions.

• Foundation for Fundamental Theorem of Calculus.

• Understanding errors and bounds in numerical integration.