Intermediate Value Theorem
The Intermediate Value Theorem (or IVT) can be used to explain and interpret the behavior of a function on an interval. Like usual in math, the Intermediate Value Theorem does just what it sounds like; it finds an intermediate value on an interval. IVT is an existence theorem, meaning it guarantees the existence of a certain value.
The Theorem
The IVT states that if a function is continuous on a closed interval [a, b], and takes on values f(a) and f(b) at the endpoints a and b, then it must also take on every value between f(a) and f(b) at least once on the interval. In other words, if you draw a continuous curve between two points on a graph, the curve must cross every y-value in between at least once. Also, if d is a number between f(a) and f(b), it states that there must be at least one c between a and b such that f(c)=d.
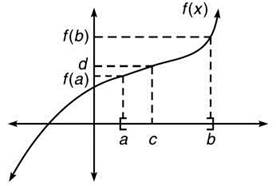
To begin IVT, always determine if the function is always continuous on the interval. If so, IVT can be used; be sure to write that the function is continuous on the interval, as it is a prerequisite and therefore part of showing your work. If it is not continuous, IVT simply cannot be used.
Common Mistakes and Confusion
Commonly confused are terms such as “increasing/decreasing” and “defined for every value.” While it may seem that these would work in place of the word “continuous,” they both can apply to a piecewise function and therefore cannot prove continuity.
Remember, IVT cannot prove that a value does not exist on an interval. It only can prove that a certain value does exist.
Utilizing a Calculator… Dos and Don’ts
Many problems involving the IVT ask if the theorem can be applied. When given a calculator, students often plug in the given function and look for the requested value on the interval, stating it can be used if the value exists. The IVT may not prove the value exists, even when it does. Because of this, the calculator should be used to quickly evaluate the endpoints of the function instead of for the graphing feature. The evaluated endpoints can be used as before to determine the applicability of IVT.