finite limits are x→±∞

• the symbol for infinity does not represent a real number; we use it to describe the behavior of a function when the values in its domain or range outgrow all finite bounds

• x→±∞: increasingly to the right or left

• a function may have multiple horizontal asymptotes (one to positive infinity and the other to negative infinity)

• in general, for a rational function of the form f(x)/g(x) where f(x) and g(x) are both polynomials, the end behavior model (EBM) is found by dividing the highest powered term of f by the highest powered term of g

  • the key to end behavior is that while the EBM ≠ the original function, it has the same limit as the original function

• 

for a function of the form f(x)/g(x), where f and g are polynomials,

• 

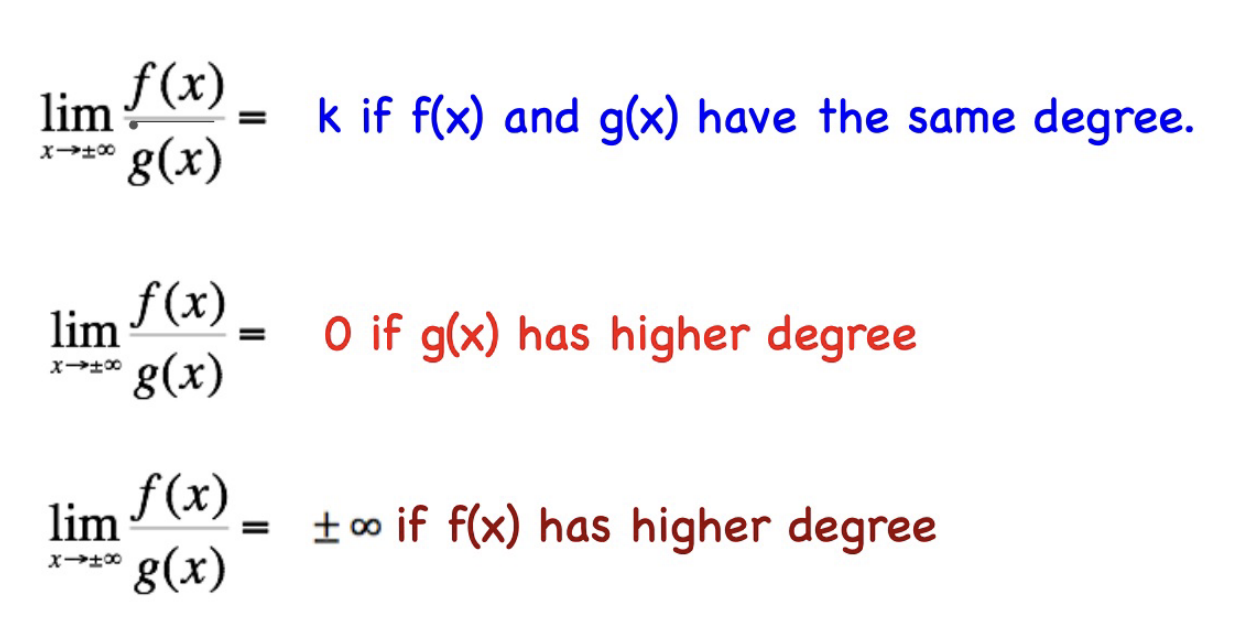
• the sandwich theorem and limit properties also hold for x→±∞