Two-Sided Limits, Squeeze Theorem, and L'Hopital's Rule

Note: This page does not include discussions of behavior at asymptotes.

To take a two-sided limit, first use a limit-taking method (duh!).

If the function is always continuous or has a removable discontinuity, skip this section and go directly to evaluating the limit. Do not pass go. Do not collect $200. However, do collect some time cause this generally makes limit-taking easier!

Otherwise, you will need to remove discontinuities first using either factoring, rationalizing the denominator, using special case limits, using the Squeeze Theorem, or using L’Hospital’s Rule (more on those farther down).

After taking the limit in this way, you usually need to evaluate it by testing the limit at the variable given. For example, if given the limit as x approaches 5, you often have to eventually plug 5 in for all the x’s.

Special Cases of Limits

There are two special cases of limits used with trigonometry and only as the limit as x approaches 0.

sin(x)/x = 1
(1-cos(x))/x = 0

Squeeze Theorem, aka “Cheese Theorem”

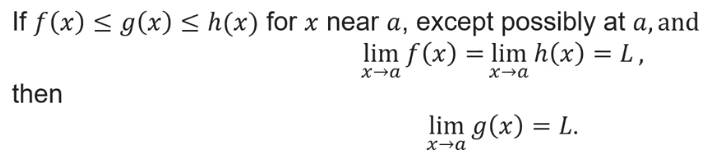
Basically, the squeeze theorem is used in a limited (pun definitely intended) number of situations. The following conditions must all be met to use the Squeeze Theorem:

The function involved in the limit you’re looking for must be between two other functions. (you must be looking for the cheese and know it’s between the bread on your grilled cheese)
The outer functions must both have a known limit. (you know where the bread is) This known limit must be the same. (the pieces of bread must be touching at at least one point)
The functions may have a removable discontinuity at the point they touch at (there may be a hole in the bread slices cause that’s how bread is made)

If all of this passes, the limit of the middle function is the same as that of the outer functions. (the cheese must be at the same point as the bread that is touching)

While cheesy (yep, another pun), try to visualize this. It is very useful for understanding how a limit works, even in situations where the Squeeze Theorem doesn’t apply.

L’Ho(s)pital’s Rule

Use L’Hopital’s Rule when finding a limit producing an indeterminate form. The indeterminate form of a limit is a mathematical expression that cannot be evaluated using algebraic manipulation alone. If you need help evaluating the patient (the limit) beyond your skills (algebra), you better go to the (L’)Ho(s)pital. For example, 0/0 or ∞/∞ are indeterminate forms. You can not determine them, so take them to the (L’)Ho(s)pital for a more specialized examination.

L'Hospital's Rule

When using L’Ho(s)pital’s rule, always include text that states what the indeterminate form produced is. For instance, if it equals 0/0, include text that says “This limit produces the indeterminate form 0/0”. The doctor can’t do anything unless they know the issue, so always take this record with any trip to the (L’)Ho(s)pital.

After finding that an indeterminate form exists and writing it down in this way, take the derivative of the numerator and denominator separately. (The nurse and doctor do separate things at the (L’)Ho(s)pital.) Next, simply finish evaluating the limit and check out of the (L’)Ho(s)pital.

If you find that the indeterminate form is still present after going to the (L’)Ho(s)pital, you can go back as many times as you need until the indeterminate form is gone.

Selecting Procedures to Determine Limits

Keep your pencil moving when trying to find a good strategy
Keep track of what you tried that didn’t work

When you see radicals, first rationalize the denominator by multiplying by a conjugate pair.
When you see polynomials, try factoring.
When you see a squared trigonometric function, try using the Pythagorean Equation (cos²(x)+sin²(x)=1) to replace it.
When you have separate functions in the numerator and denominator comprise the full function and the evaluated limit is indeterminate, apply L’Hopital’s Rule.

Note