Chapter 1: Functions
A. Definitions
A1.
- A function f is a correspondence that associates with each element a of a set called the domain one and only one element b of a set called the range.
We write f(a) = b to indicate that b is the value of f at a.
- Inputs - are the elements in the domain.
- Outputs - are the elements in the range.
- A function is often represented by an equation, a graph, or a table.
- A vertical line cuts the graph of a function in at most one point
Example :
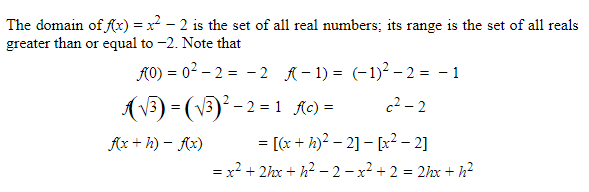
A2.
- Two functions f and g with the same domain may be combined to yield their sum and difference:
f(x) + g(x) and f(x) − g(x), also written as (f + g) (x) and (f − g) (x)
or their product and quotient: f(x)g(x) and f(x)/g(x), also written as (fg) (x) and (f /g) (x)
- The quotient is defined for all x in the shared domain except those values for which g(x), the denominator, equals zero.
Example:
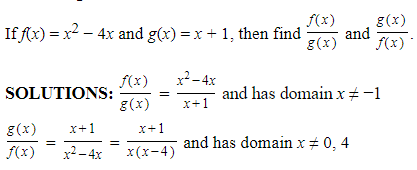
A3.
- The composition (or composite) of f with g, written as f(g(x)) and read as “f of g of x,” is the function obtained by replacing x wherever it occurs in f(x) by g(x). We also write (f ∘ g) (x) for f(g(x)).
- The domain of (f ∘ g) (x) is the set of all x in the domain of g for which g(x) is in the domain of f.
Example:

SOLUTION:

B. Special Functions
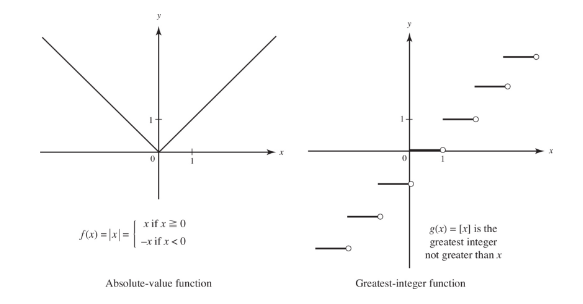
The absolute-value function f(x) = |x| and the greatest-integer function g(x) = [x] are sketched in the Figure below:
Example 8
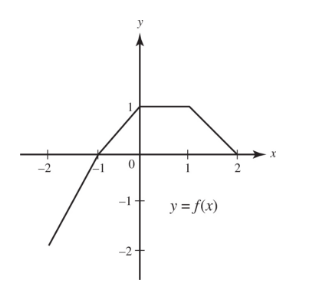
A function f is defined on the interval [−2,2] and has the graph shown in Figure 1-4.
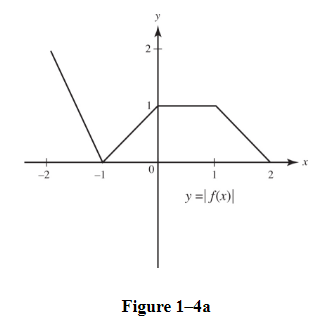
(a)Sketch the graph of y = |f(x)|.
(b)Sketch the graph of y = f(|x|).
(c)Sketch the graph of y = −f(x).
(d)Sketch the graph of y = f(−x).
SOLUTIONS:
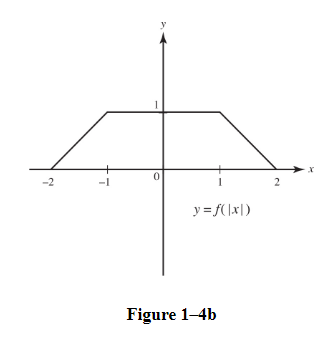

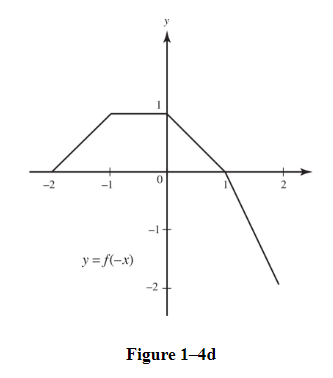
C. Polynomial and other Rational Functions
C1. Polynomial Functions
A polynomial function is of the form
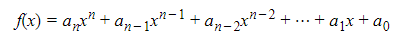
where n is a positive integer or zero, and the coefficients, a0, a1, a2, . . . an, are constants.
If an ≠ 0, the degree of the polynomial is n.
- A linear function, f(x)=mx + b, is of the first degree;
- its graph is a straight line with slope m,
- the constant rate of change of f(x) (or y) with respect to x, and b is the line’s y-intercept.
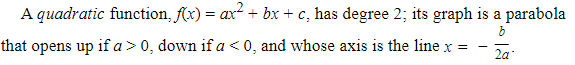
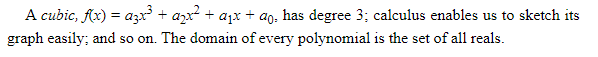
C2. Rational Functions
A rational function is of the form
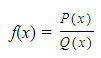
where P(x) and Q(x) are polynomials.
- The domain of f is the set of all reals for which Q(x) ≠ 0.
D. Trigonometric Functions
The fundamental trigonometric identities, graphs, and reduction formulas are given in the Appendix.
D1. Periodicity and Amplitude
The trigonometric functions are periodic.
A function f is periodic if there is a positive number p such that f(x + p) = f(x) for each x in the domain of f.
The smallest such p is called the period of f.
The graph of f repeats every p units along the x-axis.
The functions sin x, cos x, csc x, and sec x have period 2π; tan x and cot x have period π.

Example:

SOLUTIONS:
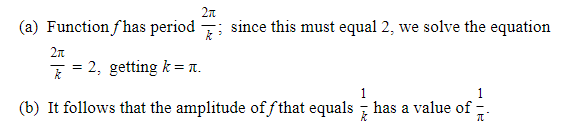
D2. Inverses
- We obtain inverses of the trigonometric functions by limiting the domains of the latter, so each trigonometric function is one-to-one over its restricted domain.
For example, we restrict
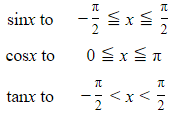
The inverse trigonometric function sin−1x is also commonly denoted by arcsin x, which denotes the angle whose sine is x. The graph of sin−1x is, of course, the reflection of the graph of sin x in the line y = x.
E. Exponential and Logarithmic Functions
E1. Exponential Functions
The following laws of exponents hold for all rational m and n, provided that a > 0, a ≠ 1:
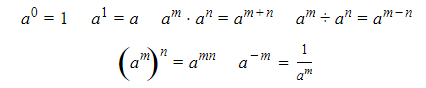
- The exponential function f(x) = ax(a > 0, a ≠ 1) is thus defined for all real x; its range is the set of positive reals.
- Of special interest and importance in calculus is the exponential function f(x) = ex, where e is an irrational number whose decimal approximation to five decimal places is 2.71828.
E2. Logarithmic Functions

The domain of log ax is the set of positive reals; its range is the set of all reals.
It follows that the graphs of the pair of mutually inverse functions y = 2x and y = log2 x are symmetric to the line y = x
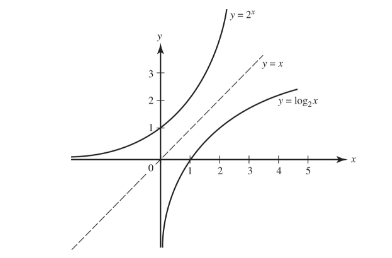
The logarithmic function loga x (a > 0, a ≠ 1) has the following properties:
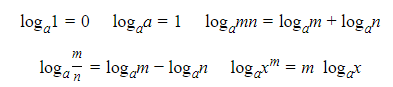
- The logarithmic base e is so important and convenient in calculus that we use a special symbol:
loge x = ln x
- Logarithms with base e are called natural logarithms. The domain of ln x is the set of positive reals; its range is the set of all reals. The graphs of the mutually inverse functions ln x and ex are given in the Appendix.
F. Parametrically Defined Functions
If the x- and y-coordinates of a point on a graph are given as functions f and g of a third variable, say t, then

are called parametric equations and t is called the parameter.
- When t represents time, as it often does, then we can view the curve as that followed by a moving particle as the time varies.
Example:
Find the Cartesian equation of, and sketch, the curve defined by the parametric equations
x=4 sint y=5 cos t (0≦t≦2π)
SOLUTION:
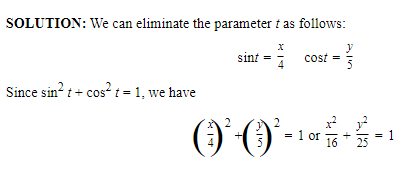

G. Polar Functions
Polar coordinates of the form (r,θ) identify the location of a point by specifying θ, an angle of rotation from the positive x-axis, and r, a distance from the origin.
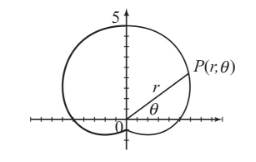
- A polar function defines a curve with an equation of the form r = f(θ).
Some common polar functions include:
Spiral
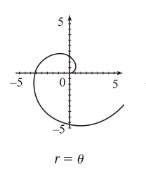
Rose
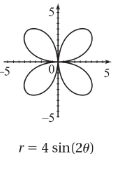
Cardioid

Limacon
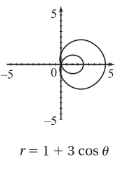
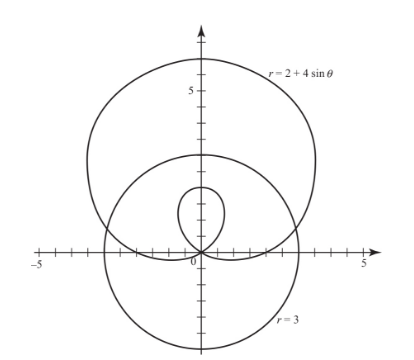
Example
Consider the polar function r = 2 + 4 sin θ.
(a)For what values of θ in the interval [0,2π] does the curve pass through the origin?
(b)For what value of θ in the interval [0,π/2] does the curve intersect the circle r = 3?
SOLUTION: