introduction to limits

limits

• the concept of limits is one of the major ideas which distinguishes calculus from lower math courses, such as algebra and geometry
• limits give us language for describing how the outputs of a function behave as the inputs approach a particular value

limit equation:

four tools exist for evaluating limits:

1. substitution
2. graphing
3. numerical approximation (table)
4. algebra (analytical approach)

evaluating limits

practice problems

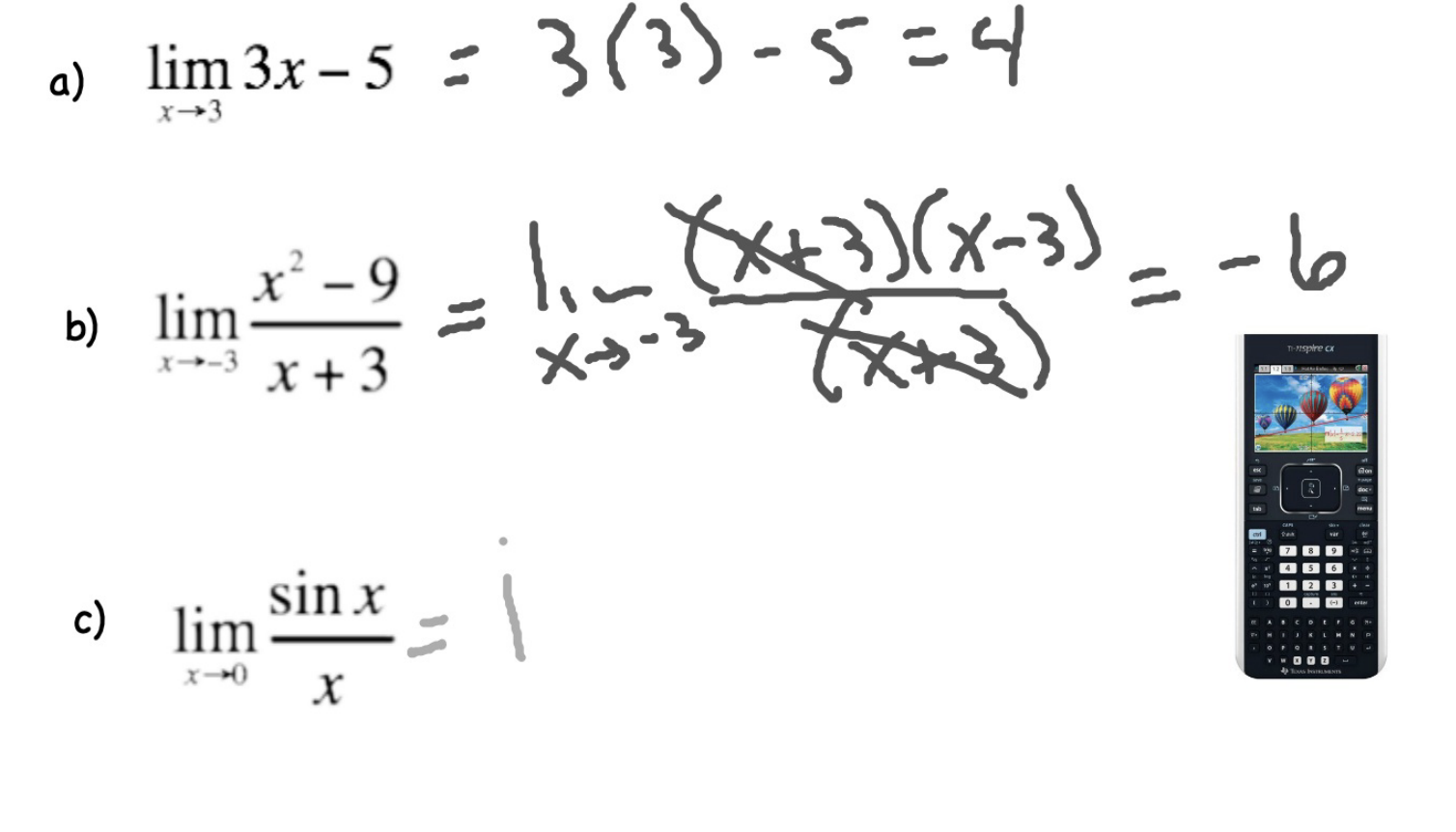
• the existence of a limit as x approaches c (x → c) never depends on how the function may or may not be defined at c

• theorem one: there are six basic facts about limits

  • sum rule: the limit of the sum of two functions equals the sum of the limits of two functions
  • difference rule: the limit of the difference of two functions equals the difference of the limits of two functions
  • product rule: the limit of a product of functions equals the product of the limit of each function
  • constant multiple rule: the limit of a constant multiple of a function equals the product of the constant with the limit of the function
  • quotient rule: the limit of a quotient of functions equals the quotient of the limit of each function
  • power rule: the limit of the nth power of a function equals the nth power of the limit of the function

  \

limits may be evaluated through the use of conjugates

• conjugate: change the sign (+ to −, or − to +) in the middle of two terms
• 

one-sided limits and the sandwich theorem

• f(x) = int x or [[x]]

• one-sided limits

  

• the sandwich theorem/the squeeze theorem

  • if g(x) ≤ f(x) ≤ h(x) for all things x ≠ c in some interval about c,

  

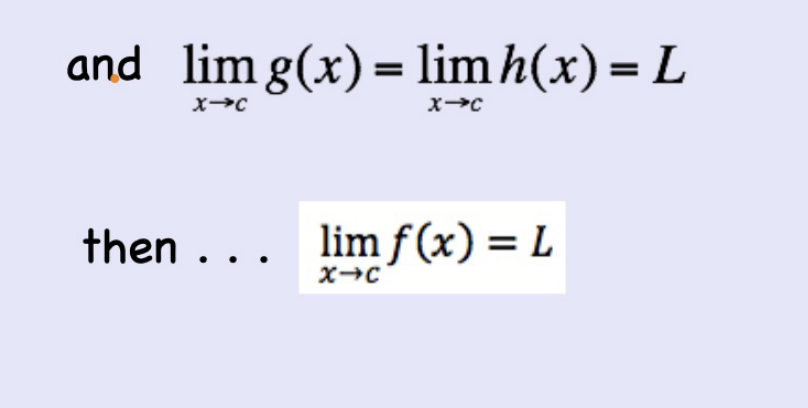
• we “trap” f(x) between two functions of known limit at c; thus, f has the same limit

\