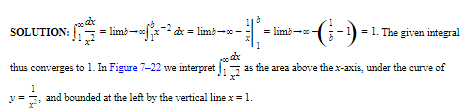A. Area

To find an area, we

1. draw a sketch of the given region and of a typical element

2. write the expression for the area of a typical rectangle

3. set up the definite integral that is the limit of the Riemann Sum of n areas as n → ∞.

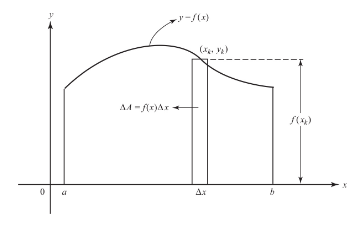
• If f(x) is nonnegative on [a,b], then f(xk) Δx can be regarded as the area of a typical approximating rectangle, and the area bounded by the x-axis, the curve, and the vertical lines x = a and x = b is given exactly by

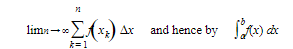
• If f(x) changes sign on the interval, we find the values of x for which f(x) = 0 and note where the function is positive, where it is negative. The total area bounded by the x-axis, the curve, x = a, and x = b is here given exactly by

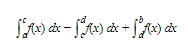where we have taken into account that f(xk) Δx is a negative number if c < x < d.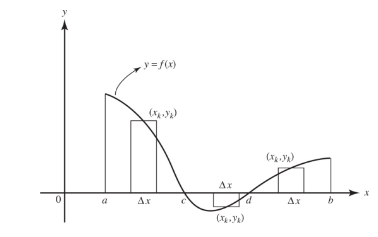

• If x is given as a function of y, say x = g(y), then the subdivisions are made along the y-axis, and the area bounded by the y-axis, the curve, and the horizontal lines y = a and y = b is given exactly by

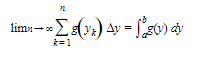
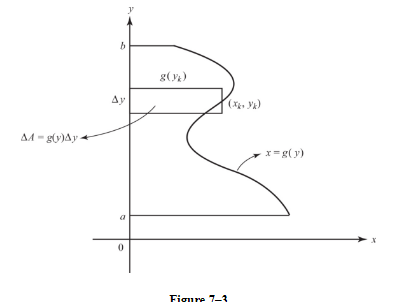
A1. Area Between Curves

To find the area between curves, we first find where they intersect and then write the area of a typical element for each region between the points of intersection. For the total area bounded by the curves y = f(x) and y = g(x) between x = a and x = e, we see that, if they intersect at [c,d], the total area is given exactly by

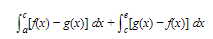
A2. Using Symmetry

Frequently we seek the area of a region that is symmetric to the x- or y-axis (or both) or to the origin. In such cases it is almost always simpler to make use of this symmetry when integrating. For example:

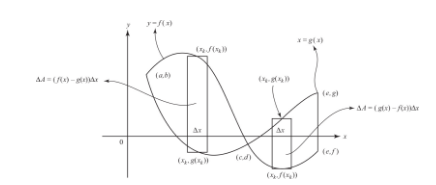
• The area bounded by the x-axis and this arch of the cosine curve is symmetric to the y-axis; hence it is twice the area of the region to the right of the y-axis.

  

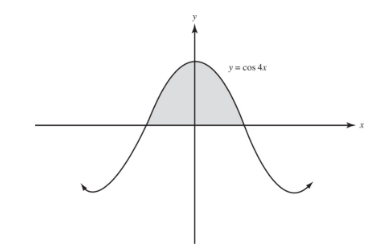
• The area bounded by the parabola and the line is symmetric to the x-axis; hence it is twice the area of the region above the x-axis.

• The ellipse is symmetric to both axes; hence the area inside the ellipse is four times the area in the first quadrant.

B. Volume

B1. Solids with Known Cross Sections

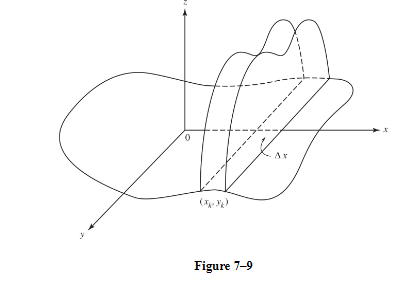
• If the area of a cross section of a solid is known and can be expressed in terms of x, then the volume of a typical slice, ΔV, can be determined.

• The volume of the solid is obtained, as usual, by letting the number of slices increase indefinitely. In Figure 7-9, the slices are taken perpendicular to the x-axis so that ΔV = A(x) Δx, where A(x) is the area of a cross section and Δx is the thickness of the slice.

Example:

A solid has as its base the circle x2 + y2 = 9, and all cross sections parallel to the x-axis are squares. Find the volume of the solid.

SOLUTION:

B2. Solids of Revolution

• A solid of revolution is obtained when a plane region is revolved about a fixed line, called the axis of revolution.

There are two major methods of obtaining the volume of a solid of revolution: “disks” and “washers”.

1. DISKS

   The region bounded by a curve and the x-axis is revolved around the x-axis, forming the solid of revolution seen in Figure 7-11. We think of the “rectangular strip” of the region at the left as generating the solid disk, ΔV (an element of the volume), shown at the right.

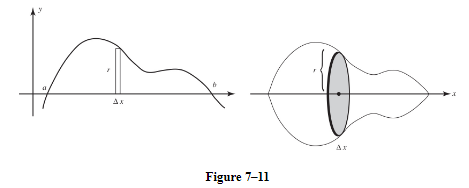
This disk is a cylinder whose radius, r, is the height of the rectangular strip, and whose height is the thickness of the strip, Δx. Thus

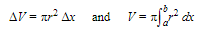
Example :

Find the volume of a sphere of radius r.

SOLUTION:

2. WASHERS

   A washer is a disk with a hole in it. The volume may be regarded as the difference in the volumes of two concentric disks. As an example, consider the volume of the solid of revolution formed when the region bounded by the two curves seen in Figure 7-14 is revolved around the x-axis. We think of the rectangular strip of the region at the left as generating the washer, ΔV (an element of the volume), shown at the right.

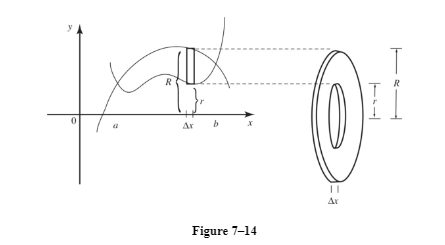
This washer’s height is the thickness of the rectangular strip, Δx. The washer is a disk whose outer radius, R, is the distance to the top of the rectangular strip, with the disk of inner radius r (the distance to the bottom of the strip) removed. Thus:

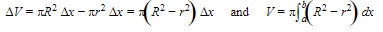
Example :

Find the volume obtained when the region bounded by y = x2 and y = 2x is revolved about the x-axis.

SOLUTION:

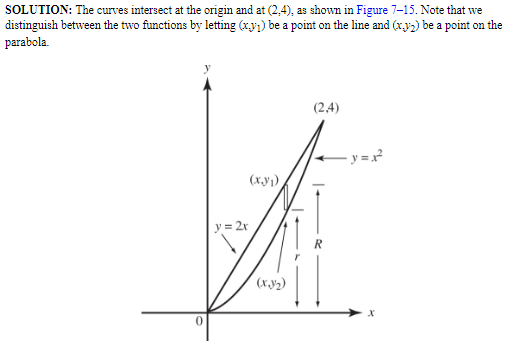
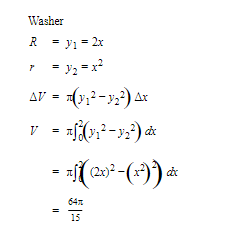
C. Length of Curve

Example :

Find the length, to three decimal places, of the curve of y = *x^*3/2 from x = 1 to x = 8.

SOLUTION:

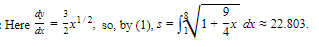
D. Improper Integrals

There are two classes of improper integrals:

1. those in which at least one of the limits of integration is infinite (the interval is not bounded)

2. those of the type ∫baf(x) dx, where f(x) has a point of discontinuity (becoming infinite) at x = c, a ≦ c ≦ b (the function is not bounded)

Illustrations of improper integrals of class (1) are:

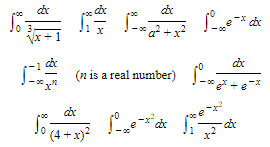
The following improper integrals are of class (2):

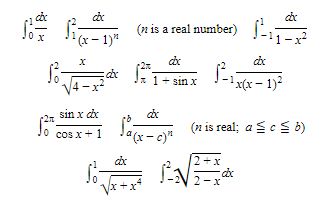
Sometimes an improper integral belongs to both classes. Consider, for example,

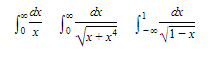
In each case, the interval is not bounded and the integrand fails to exist at some point on the interval of integration.

Note, however, that each integral of the following set is proper:

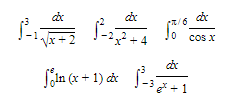
The integrand, in every example above, is defined at each number on the interval of integration.

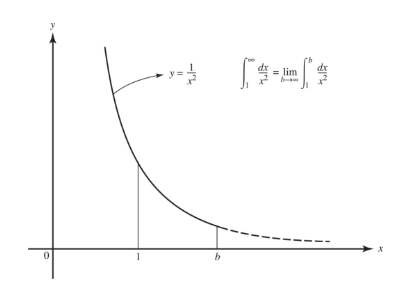
Improper integrals of class (1), where the interval is not bounded, are handled as limits:

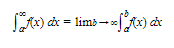
where f is continuous on [a,b]. If the limit on the right exists, the improper integral on the left is said to converge to this limit; if the limit on the right fails to exist, we say that the improper integral diverges (or is meaningless).

Example:

Find

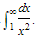
SOLUTION: