How to Use the Squeeze Theorem (and when!)

The Squeeze Theorem (or Sandwich Theorem) is a fundamental tool in calculus used to evaluate limits of functions. It is particularly useful when a function's behavior is difficult to analyze directly, but it can be "squeezed" between two simpler functions whose limits are known and equal at a specific point.

1. What is the Squeeze Theorem?

The Squeeze Theorem helps determine the limit of a function f(x) by comparing it to two simpler functions, g(x) and h(x), where:

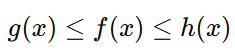
for all x in an interval around a, except possibly at x=a.

If:

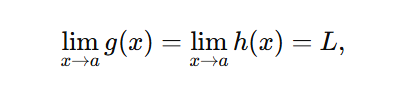
then:

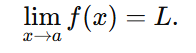
This theorem also applies to limits as x→∞ or x→−∞.

2. When to Use the Squeeze Theorem

You should consider using the Squeeze Theorem in the following scenarios:

• Bounding a Difficult Function: Use when f(x) is hard to evaluate directly, but bounds g(x) and h(x) are easier to analyze.

• Oscillatory Functions: For functions like f(x)=x²sin⁡(1/x), where oscillations complicate direct evaluation.

• Behavior Near Discontinuities: To analyze limits at points of irregular behavior.

• Small Perturbations: When small terms complicate direct computation but diminish as x→a or x→∞.

3. Steps to Apply the Squeeze Theorem

Step 1: Find Bounding Functions

Identify two functions g(x) and h(x) such that g(x) ≤ f(x) ≤ h(x).

Step 2: Check Validity of Inequalities

Ensure the inequalities hold in a neighborhood around aaa, excluding aaa itself if necessary.

Step 3: Calculate the Limits of the Bounds

Compute:

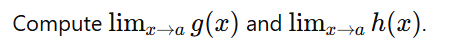
Step 4: Conclude Using the Theorem

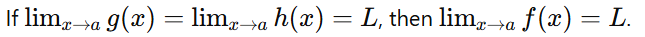
4. Examples

Example 1: A Trigonometric Limit

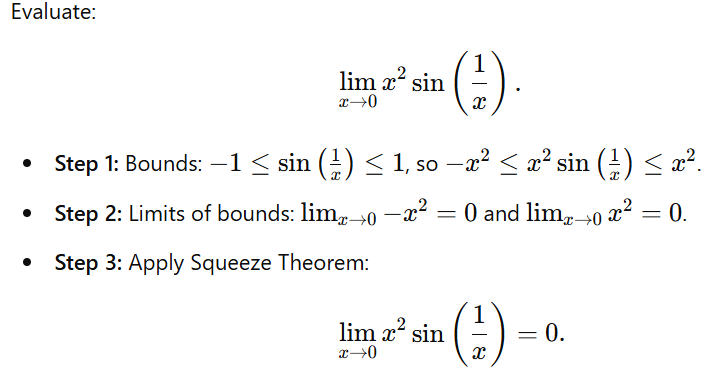
Example 2: A Rational Function

5. Common Mistakes

1. Failing to Establish Valid Bounds
   Ensure g(x) ≤ f(x) ≤ h(x) holds in the specified interval.

2. Mismatch of Limits
   Verify both bounds converge to the same value.

3. Misinterpreting Oscillation
   Understand that bounded oscillatory behavior can often be squeezed.

6. Why the Squeeze Theorem Works

The intuition behind the theorem lies in the behavior of limits. If f(x) is always trapped between g(x) and h(x), and both g(x) and h(x) approach the same value, f(x) is compelled to approach that value too. This is particularly useful when f(x) oscillates or behaves erratically.

7. Applications of the Squeeze Theorem

• Physics: Analyzing small oscillations or limits in wave equations.

• Engineering: Studying systems with bounded perturbations.

• Mathematics: Proving limit-related theorems and establishing convergence.

8. Summary

The Squeeze Theorem is a powerful technique for evaluating tricky limits. To use it effectively:

• Find appropriate bounding functions.

• Ensure the bounds and limits align correctly.

• Use the theorem when direct computation is infeasible due to oscillations, irregular behavior, or complex expressions.

By mastering this theorem, you gain a versatile tool for tackling challenging problems in calculus!