Chapter 8: Further Applications of Integration
A. Motion Along a Straight Line
If the motion of a particle P along a straight line is given by the equation s = F(t), where s is the distance at time t of P from a fixed point on the line, then the velocity and acceleration of P at time t are given respectively by
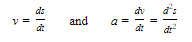
If we know that particle P has velocity v(t), where v is a continuous function, then the distance traveled by the particle during the time interval from t = a to t = b is the definite integral of its speed:
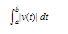
If v(t) ≧ 0 for all t on [a,b] (i.e., P moves only in the positive direction), then (1) is equivalent to ∫bav(t) dt; similarly, if v(t) ≦ 0 on [a,b] (P moves only in the negative direction), then (1) yields −∫bav(t) dt.. If v(t) changes sign on [a,b] (i.e., the direction of motion changes), then (1) gives the total distance traveled. Suppose, for example, that the situation is as follows
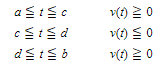
Then the total distance traveled during the time interval from t = a to t = b is exactly
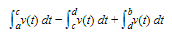
The displacement or net change in the particle’s position from t = a to t = b is equal, by the Fundamental Theorem of Calculus (FTC), to
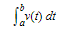
Example :
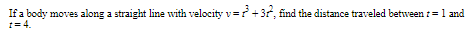
SOLUTION:
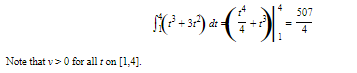
B. Motion along a Plane Curve
If the motion of a particle P along a curve is given parametrically by the equations x = x(t) and y = y(t), then at time t the position vector R, the velocity vector v, and the acceleration vector a are:
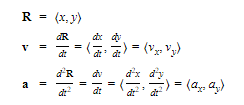
The components in the horizontal and vertical directions of R, v, and a are given, respectively, by the coordinates in the corresponding vector. The slope of v is dy/dx;; its magnitude,
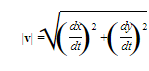
is the speed of the particle, and the velocity vector is tangent to the path. The slope of a is d²y/dt² d²x/dt². The distance the particle travels from time t1 to t2 is given by
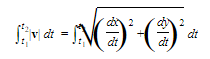
Example:
Suppose a projectile is launched from the origin at an angle of elevation α and initial velocity v0. Find the parametric equations for its flight path.
SOLUTION:

C. Other Applications of Remiann Sums
- We will continue to set up Riemann Sums to calculate a variety of quantities using definite integrals. In many of these examples, we will partition into n equal subintervals a given interval (or region or ring or solid or the like), approximate the quantity over each small subinterval (and assume it is constant there), then add up all these small quantities.
- Finally, as n → ∞, we will replace the sum by its equivalent definite integral to calculate the desired quantity.
Example :
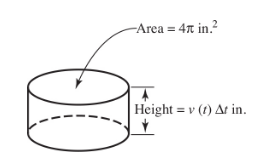
Amount of Leaking Water. Water is draining from a cylindrical pipe of radius 2 inches. At t seconds the water is flowing out with velocity v(t) inches per second. Express the amount of water that has drained from the pipe in the first 3 minutes as a definite integral in terms of v(t).
SOLUTION:
We first express 3 minutes as 180 seconds. We then partition [0,180] into n subintervals each of length Δt. In Δt seconds, approximately v(t) Δt inches of water have drained from the pipe. Since a typical cross section has area 4π in.2, in Δt seconds the amount that has drained is
(4π in.2) (v(t) in./sec)(Δt sec) = 4πv(t) Δt in.3
The sum of the n amounts of water that drain from the pipe, as n → ∞, is ∫18004πv(t) dt; the units are cubic inches (in.3).
D. FTC: Definite Integral of a Rate is Net Change
If f is continuous and f(t)=dF/dt, then we know from the FTC that
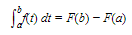
The definite integral of the rate of change of a quantity over an interval is the net change or net accumulation of the quantity over that interval. Thus, F(b) − F(a) is the net change in F(t) as t varies from a to b.
Example :
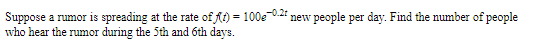
SOLUTION:
