Related Rates

Related rates is a math concept that deals with the measurement of how the rate of change of one quantity is related to the rate of change of another quantity. In other words, it involves finding the rate of change of one variable with respect to another variable. The key to solving related rates problems is identifying the variables involved and setting up an equation that relates them.

How Rates of Change are Related

All rates of change in related rates problems involve not only the variables visible in the equation, but also time. Because of this, time is how rates are related to one another. To find the relationship, do implicit differentiation on an equation with respect to time.

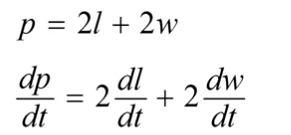
In the example, the perimeter is changing. The implicit differentiation proves that the rate of the perimeter change, length change, and width change are all related to one another.

Determining the Equation for a Related Rates Problem

As you can see, determining the equation that applies to a problem is very important. The most common equations that will be needed are geometric equations for perimeter, area, or volume. This is because related rates problems are a type of application problem that generally applies to growing or shrinking objects or shapes. There is no fully comprehensive list of equations, but many of the most common ones are included below.

Perimeter

• Square/Rectangle: P = 2l+2w

Area

• Square: A = s²
• Rectangle: A = lw
• Triangle: A = 1/2bh
• Circle: A = πr²

Volume

• Cube: V = s³
• Rectangular prism: V = lwh
• Sphere: V = (4/3)πr³
• Cylinder: V = πr²h
• Cone: V = (1/3)πr²h

Pythagorean Theorem

• a² + b² = c²

Angles (only apply when dealing with right triangles)

The sides used in the equation are commonly listed as x and y in a problem. However, no matter the variable, these formulas apply to the sides relative as described to the angle being found.

• Sine: sin(θ) = opposite/hypotenuse
• Cosine: cos(θ) = adjacent/hypotenuse
• Tangent: tan(θ) = opposite/adjacent
• Cosecant: csc(θ) = hypotenuse/opposite
• Secant: sec(θ) = hypotenuse/adjacent
• Cotangent: cot(θ) = adjacent/opposite

Setting Up a Related Rates Problem

To set up a related rates problem, follow these steps:

1. Identify all the variables involved in the problem and assign them variables (usually letters).
2. Write down these variables with any values given in the problem.
3. Write down the rate at which each variable is changing. If a rate is not given, write that you don’t know what it equals (with a question mark, for example).
4. Write down the variable and rate you are looking for.
5. Write an equation that relates the variables from Step 1 with the variable you are looking for in Step 4. (Remember, many of these equations are included above this section).
6. Do implicit differentiation on both sides of the equation with respect to time.
7. Substitute in all known values and solve for whatever is left. Remember to always include units and consider your answer logically.

\