Chapter 9 - Properties of Gases
9.1 Properties of Gases
The volume a gas occupies is inversely proportional to its pressure
the pressure of a gas in a rigid container is directly proportional to its absolute temperature
the gas pressure inside a rigid container at a constant temperature is directly proportional to the quantity of moles
the volume of a gas is inversely proportional to the pressure applied
all gases are miscible with all other gases - homogenous mixtures
at a given temperature and pressure, the densities of gaseous substances are directly proportional to their molar masses and are much lower than their densities in the solid or liquid state
gases expand to occupy the entire volume of their containers
gases effuse at rates inversely proportional to the molar masses of gases - smallest molar masses effuse most rapidly
9.2 Effusion, Diffusion and Kinetic Molecular Theory of Gases
effusion: the process by which a gas escapes from its container through a tiny hole into a region with low pressure
graham’s law of effusion: effusion rate of gas is inversely proportional to the square root of its molar mass and its density
law of effusion and law of diffusion are interchangeable
 kinetic molecular theory: behavior of gases is directly related to the basis of motion of the particles that make up the gas
kinetic molecular theory: behavior of gases is directly related to the basis of motion of the particles that make up the gas
individual gas molecules treated as point masses
gas is mostly empty space
gas molecules are constantly and randomly moving throughout its occupied space and continually collide with each other and the container walls
collisions are elastic, meaning there is no net transfer of energy to the walls - average kinetic energy of all the balls is the same immediately after the collision as it was before
intermolecular forces are negligible, assuming particles don’t interact at all
average kinetic energy of particles is proportional to absolute temperature of the gas - all populations of gas molecules at the same temperature have same average kinetic energy
determined by KE=.5(m)(v)^2
most probable speed: peak in graph correlates to the speed of the largest quantity of molecules
average speed: arithmetic mean of all individual speeds, slightly higher than most probable speed
root-mean-square speed: square root of the average of all squared speeds of all gas particles, equal to the speed of the average kinetic energy of all gas particles
universal gas constant: R=8.314 (kg*m^2)/(s^2mol**K)
diffusion: spread of one substance through another - occurs when there are differences in composition of the mixture of gases within occupied space
mean free path: average distance a particle can travel through air or gas before colliding with another particle, depends on density and pressure
at 1 atm, mean free path: 6.8*10^-8
9.3 Atmospheric Pressure
Pressure: P=F/A where F is force and A is surface area
atmospheric pressure varies from place to place and weather conditions
1 atm = 760 mmHg = 760 torr
Barometer: instrument that is measured with a barometer
Manometer: measures pressure exerted by a gas, displayed by delta h = P sample - P atm
9.4 Relating P, V, T in the Gas Laws
Boyles Law: Pressure is inversely related to volume at a constant T and n.
P1V1 = P2V2
Charles’ Law: Volume of a fixed quantity of gas is directly proportional to the temperature (in K) when pressure and n are constant
V1/T1 = V2/T2
Avogadro’s Law: Pressure is proportional to moles of gas when temperature and volume are constant
Amontons’ Law: Volume is proportional to its temperature at constant pressure and volume; pressure is directly proportional to temperature if volume is held constant
P1/T1 = P2/T2
9.5 Combined Gas Law
Combined Gas Law: (P1V1)/T1 = (P2V2)/T2
9.6 Ideal Gases and the Ideal Gas Law
Ideal Gases: gases that behave in accordance with combined gas law; assumed that volumes of individual gas particles are insignificant
Ideal Gas Law: PV=nRT
Standard Temperature and Pressure (STP): 0 degrees C and 1 bar of pressure; one mol of an idea gas will occupy 22.4 L
9.7 Densities of Gases
Density of any gas at STP can be found by dividing its molar mass by the molar volume
d=(MP)/(RT)
9.8 Gases in Chemical Reactions
we can use the ideal gas law to find n, which is number of moles, which we can then use to perform stoichiometric calculations
9.9 Mixtures of Gases
Partial Pressure: pressure exerted by each individual gas in a mixture of gases
Atmospheric Pressure: sum of partial pressures of all gases in the air
Dalton’s Law of Partial Pressures: total pressure of any mixture of gases is the sum of the partial pressures in the mixture
Mole Fraction: abundance of a specific component i in a mixture of gases
xi = (ni)/(ntotal)
9.10 Real Gases
real atoms and molecules experience greater intermolecular forces at high pressures and low temperatures, causing deviations from ideal gas behavior
deviations are determined by the different intermolecular forces experienced
atoms and molecules have volume and this volume becomes a significant fraction of total volume at high pressures as particles become more condensed
van der Waals Equation: corrects for intermolecular forces and volume taken up by particles
van der Waals Forces: intermolecular forces that contribute to the value of the a constant of a gaseous substance
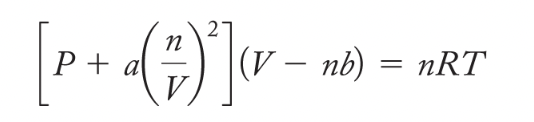
 Knowt
Knowt
