Chapter 5 - Magnetism and Electromagnetic Induction

Magnetic Fields

• All magnets have South and North poles

  • If you took a magnet such as a rectangular-shaped bar magnet, you are not separating the poles - you are creating two magnets that still have North and South poles

• Magnetism and static electricity

  • Similarities:
  • Magnets and charges exert equal and opposite forces on each other
  • Magnetic and electric fields extend into infinity and get weaker with increased distance
  • Differences:
  • Magnetic fields only affect moving charges whereas electric fields can affect both stationary and moving charges
  • The force exerted by magnetic fields is perpendicular to both the velocity of the charge and the direction of the magnetic field
  • Magnetic field lines are loops instead of lines like in electric fields

• Magnetic Field lines

  • Magnetic field lines are loops that point away from the North and toward the South

    

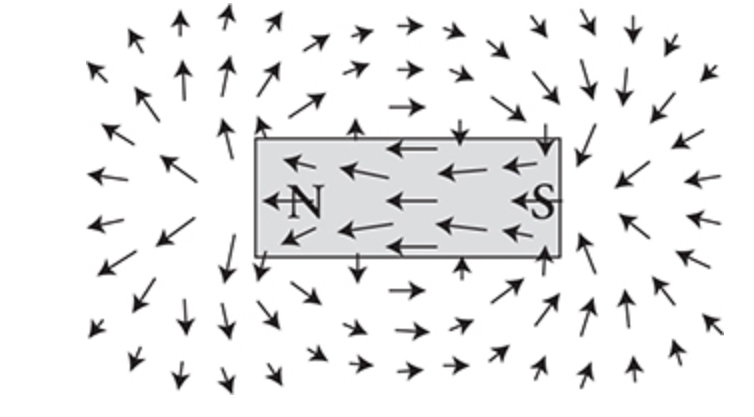
  • Iron filings gather on these magnetic field lines, creating patterns visible to the human eye

  • Like electric field lines, longer arrows indicate larger field strength

• What creates magnetic fields?

  • Moving charges
  • For bar magnets, these charges are the electrons circling the nucleus of atoms
  • In wires, current serves as moving charges

• 3-D nature

  • Magnetic fields are 3D which is often hard to show on paper

  • In the exam, a dot with a circle (the circle is most often there but it could just be a dot) around it indicates a magnetic field coming out of the page (think of an arrow head coming at you)

  • An X indicates a magnetic field going into the page (think of the back of an arrow)

    

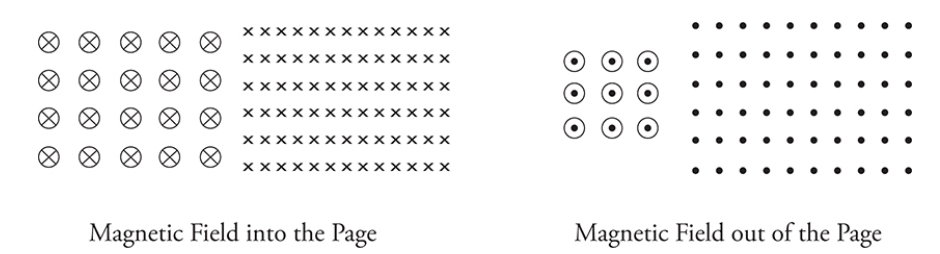
Applications of Magnetic Fields

• Dipoles of the Earth

  • The magnetic south pole is actually the geographic north pone and vice versa

• The magnetic field in a straight wire with current

  • The magnetic field forms circles in the plane perpendicular to the length of the wire

  • Picture washers on a wire - those represent circles of the magnetic field

  • The right-hand rule

    

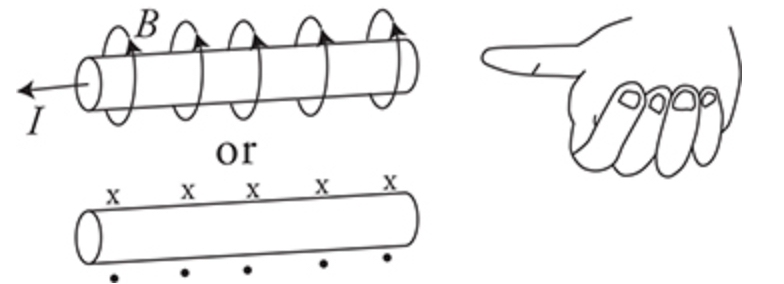
  • Grasp a pencil with your right hand

  • Your fingers will curl around the pencil in the same direction the magnetic field curls

    • If you imagine a wire with current pointing left, the magnetic field will be represented with X’s on top of the wire and dots below the wire (also known as counterclockwise)

  • Your thumb will point in the direction of the current

  • ==B = 𝜇I/(2πr)==

  • B: magnetic field

  • 𝜇: vacuum permeability (4π x 10^-7)

  • I: Current

  • r: distance between enter of wire to where you’re trying to find the field strength

• Solenoid

  • Solenoid: a coil of wire created by wire looped circularly multiple times
  • Solenoids hooked up to a battery creates a dipole magnetic field like a bar magnet

• Force on a moving charge

  • If the velocity of a moving particle is perpendicular to the magnetic field, a magnetic force is exerted on the moving charge

  • ==F = qvBsin(θ)==

  • F: magnetic force

  • q: charge of particle

  • v: velocity

  • B: magnetic field

  • θ: angle between velocity and magnetic field vectors

  • Right hand rule - “flat finger” rule

    

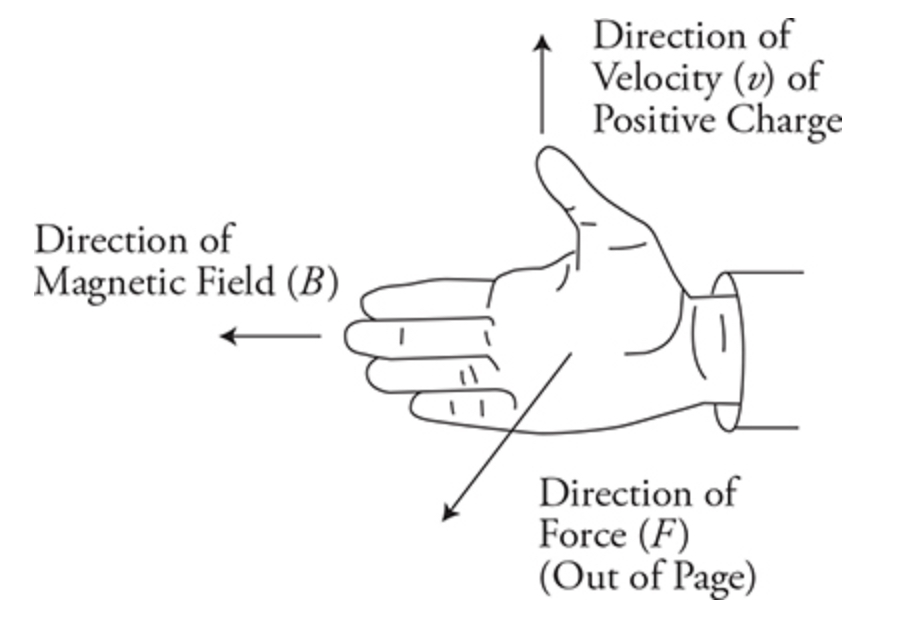
  • Fingers point in the direction of the magnetic field

  • Thumb points in the direction of the velocity for the positive charge

  • Palm points in the direction of the force

  • The right hand rule works for positive particles but for negative particles, the same rules apply if you use your left hand

  • When acceleration is perpendicular to the velocity, as is the case because the magnetic force is perpendicular to the velocity, the acceleration is centripetal

• Force on a current-carrying wire from an outside magnetic field

  • ==F = ILsin(θ)B==
  • F: magnetic force
  • L: length of the wire
  • B: magnetic field
  • I: current
  • θ: angle between the current and magnetic field

• The force between two parallel wires

  • To solve problems like this, find the directions of the magnetic field around Wire B and determine the effects on Wire A
  • The forces on the wires are equal and opposite in direction
  • ==B = 𝜇I/(2πr)==
  • B: Magnetic field from wire B
  • I: Current from wire B
  • r: distance between wires A and B
  • ==F = ILsin(θ)B==
  • F: magnetic force on wire A from wire B
  • I: current through wire A
  • L: length of wire (lengths of wire A and B are the same)
  • B: magnetic field from wire B

• Mass Spectrometer

• Remember that magnetic forces give charges a centripetal acceleration

  • This means the magnetic force only changes the direction of the charge without altering the magnitude of the velocity
  • The path of the charge then becomes circular

• Fc = Fb

  • Fc: centripetal force
  • Fb: magnetic force

• ==mv^2/r = qvB==

  • m: mass of the particle
  • v: velocity
  • r: radius of the circular path
  • q: charge
  • B: magnetic field
  • Therefore, ==r = mv/(qB)==

• If part of the velocity is parallel to the field (theta is not 90 degrees), the charge will take a helical path

• Mass Spectrometer: a device used to determine the charge to mass of a particle by arcing them in a magnetic field and finding the radius of its path

Magnetic Flux

• Magnetic Flux: a measure of the magnetic field passing through an area
  • Measured in Webers
• Magnetic field strength (magnetic flux density) multiplied by area is equal to magnetic flux
  • ==ɸ = Bcos(θ)A==
  • ɸ: magnetic flux
  • B: magnetic field
  • θ: angle between the magnetic field and the “window” of magnetic flux we’re measuring

Electromagnetic Induction

• Electromotive force
  • ==ε = Blv==
  • ε: electromotive force
  • B: magnetic field
  • l: length of the wire in the magnetic field
  • v: velocity of the wire
  • The movement of a wire through a magnetic field can produce an electromotive force
  • Other ways to use electromagnetic induction:
  • Changing magnetic field strength
  • Changing the flux area of a loop
  • Turning the loop
  • ==ε = -N(Δɸ/Δt)==
  • N: number of turns in the wire around the loop
  • For rectangular loops:
  • ==ε = BLv==
    • ε: electromotive force
    • L: length of the rectangle side that is entering the magnetic field
    • B: magnetic field
    • v: velocity
• Lenz’s Law: The direction of the induced current opposes any change in flux
  • If we move a loop with zero magnetic field near a magnetic field coming out of the page, the induced current will create a magnetic field into the page within the loop to oppose the increased magnetic field out of the page
  • When the loop stops moving and is completely in the region with the magnetic field, there is no induced emf with no changing flux
• Uses for electromagnetic induction:
  • Generation of electricity
  • In microphones and speakers
  • To run motors
  • In MRIs
  • On credit cards
  • Point is: electromagnetic induction is very important in everyday use

Magnetic Behavior

• Ferromagnetism
  • Ex: iron, nickel. and cobalt
  • Localized regions called domains are inside this material
  • In an external magnetic field, the domains align, amplifying it
  • Domains can grow enough to create a permanent magnet
  • Magnets strongly attract ferromagnetic materials
• Paramagnetism
  • Unlike ferromagnetic materials, paramagnetic materials don’t form permanent magnets
  • Magnets weakly attract paramagnetic materials
  • The domains still align with the external magnetic field
• Diamagnetism
  • Internal properties align opposite to the external field - cancel out that part of the magnetic field
  • Ex: water, graphite
  • Magnets weakly repel diamagnetic materials