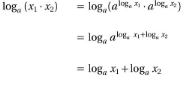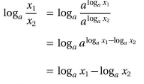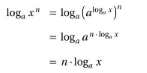Groei + logaritmen
📏 Lineaire groei
ontstaat de volgende waarde uit de vorige door optelling met een getal. Dat getal is constant als de tijdsintervallen even groot zijn. De grafiek is een rechte.
rekenkundige rij
❌ Exponentiële groei
Ontstaat de volgende waarde uit de vorige door vermenigvuldiging met een getal. Dat getal heet de groeifactor en is constant als de tijdsintervallen even groot zijn.
meetkundige rij
Groeifactora
opname 1+ p/100
Afname: 100[a-1
exponentiële functies:
Is a element van positieve |R zonder 0, dan noemen de reële functie f met ƒ(x) = a^x een exponentiële functie met grondtal of groeifactor a.
 a is eignelijk ook gewoon de groeifactor.
a is eignelijk ook gewoon de groeifactor.
exponentievergelijkingen:
een vergelijking waarbij x in een exponent voorkomt
zelfde grondtal → exponenten worden grondtal
1X GRONDTAL IEDERE KANT
verdubbelingstijd: bij exponentiële groei is de tijd waarin de hoeveelheid verdubbeld
Beginwaarde verdubbelen = y
🪵 logaritmen
de logaritme met grondtal a is een element van een strikt positief reëel getal is de exponent van de macht waartoe we a moeten verheffen om dat getal te krijgen.
mn eigen regels
k d G = omgekeerd
x Br = - y
→ kunnen worden samengebruikt
Rekenregels met bewijs
regel | bewijs |
|---|---|
loga (X1*X2) = loga X1+log X2 |
|
logA X1/X2 = loga X1- loga X2 |
|
loga X^n= n* loga X |
|
logbX = logaX / loga b |
|
Logaritmische functies
is a een element van een strikt positief reëel getal zonder 1, dan doemen we de reële functie f(x) met logaX de logaritmische functie met grondtal a.

Exponentiële vergelijkingen via logaritmen
doe * log aan alle kanten, pas dan rekenregels toe
Groei + logaritmen
📏 Lineaire groei
ontstaat de volgende waarde uit de vorige door optelling met een getal. Dat getal is constant als de tijdsintervallen even groot zijn. De grafiek is een rechte.
rekenkundige rij
❌ Exponentiële groei
Ontstaat de volgende waarde uit de vorige door vermenigvuldiging met een getal. Dat getal heet de groeifactor en is constant als de tijdsintervallen even groot zijn.
meetkundige rij
Groeifactora
opname 1+ p/100
Afname: 100[a-1
exponentiële functies:
Is a element van positieve |R zonder 0, dan noemen de reële functie f met ƒ(x) = a^x een exponentiële functie met grondtal of groeifactor a.
 a is eignelijk ook gewoon de groeifactor.
a is eignelijk ook gewoon de groeifactor.
exponentievergelijkingen:
een vergelijking waarbij x in een exponent voorkomt
zelfde grondtal → exponenten worden grondtal
1X GRONDTAL IEDERE KANT
verdubbelingstijd: bij exponentiële groei is de tijd waarin de hoeveelheid verdubbeld
Beginwaarde verdubbelen = y
🪵 logaritmen
de logaritme met grondtal a is een element van een strikt positief reëel getal is de exponent van de macht waartoe we a moeten verheffen om dat getal te krijgen.
mn eigen regels
k d G = omgekeerd
x Br = - y
→ kunnen worden samengebruikt
Rekenregels met bewijs
regel | bewijs |
|---|---|
loga (X1*X2) = loga X1+log X2 |
|
logA X1/X2 = loga X1- loga X2 |
|
loga X^n= n* loga X |
|
logbX = logaX / loga b |
|
Logaritmische functies
is a een element van een strikt positief reëel getal zonder 1, dan doemen we de reële functie f(x) met logaX de logaritmische functie met grondtal a.

Exponentiële vergelijkingen via logaritmen
doe * log aan alle kanten, pas dan rekenregels toe
 Knowt
Knowt