Lesson 1: Basic Matrix Operations

• Adding and Subtracting Matrices

  • A matrix is a rectangular arrangement of numbers

  • The dimensions of a matrix with m rows and n columns are m × n (read "m by n")

  • The numbers in a matrix are its elements

  • Two matrices are equal when their dimensions are the same and the elements are equal

  • To add or subtract two matrices, add or subtract their corresponding elements

    • Add or subtract matrices only when they have the same dimensions

    • 

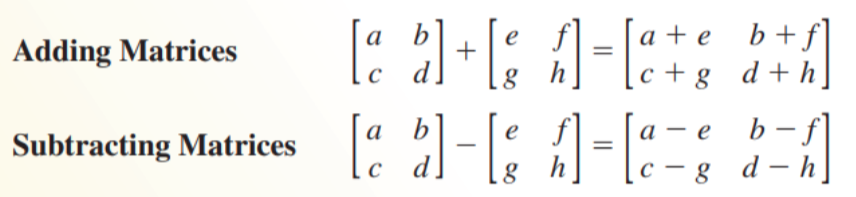
• Scalar Multiplication

  • When working with matrices, a real number is called a scalar

  • To multiply a matrix by a scalar, multiply each element in the matrix by the scalar

  • This is called scalar multiplication

• Scalar Matrix Equations

  • Using the definition of equal matrices, you can equate the elements in corresponding portions of two matrices that are equal

Lesson 2: Multiplying Matrices

• Multiplying Matrices

  • The product of two matrices A  and B is defined provided the number of columns in A is equal to the number of rows in B

  • If A is an m × n matrix and B is an n × p matrix, then the product AB is an m × p matrix

  • 

  • To find the element in the ith row and jth column of the product matrix AB, multiply each element in the ith row of A by the corresponding element in the jth column of B, then add the products

  • 

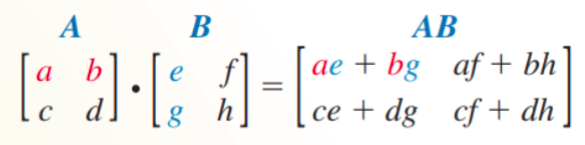
  • Matrix multiplication is not commutative

  • 

Lesson 3: Matrix Determinants and Cramer's Rule

• The Determinant of a Matrix

  • Determinant of a 2x2 Matrix

    • The determinant of a 2x2 matrix is the difference of the products of the elements on the diagonals shown

    • 

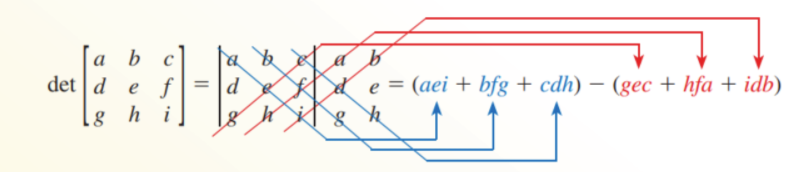
  • Determinant of a 3x3 Matrix

    • Repeat the first two columns to the right of the determinant

    • Subtract the sum of the red products from the sum of the blue products

    • 

  • Cramer's Rule

    • You can use determinants to solve a system of linear equations

    • The method, called Cramer's Rule, uses the coefficient matrix of the linear system

    • 

    • Cramer's Rule for a 2x2 System

      • Let A be the coefficient matrix of the linear system

      • 

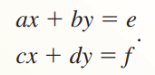
      • If det A ≠ 0, then the system has exactly one solution:

      • 

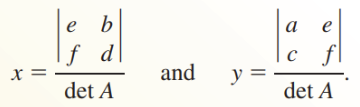
      • Note that the numerators for x and y are the determinants of the matrices formed by replacing the values of the x and y coefficient columns, respectively, with the columns of the constant values

    • Cramer's Rule for a 3x3 System

      • Let A be the coefficient matrix of the linear system shown below

      • 

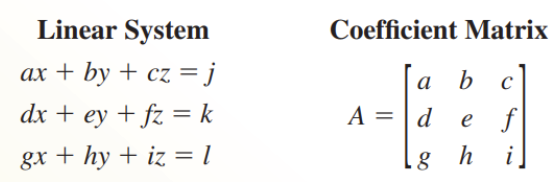
      • If det A ≠ 0, then the system has exactly one solution:

      • 

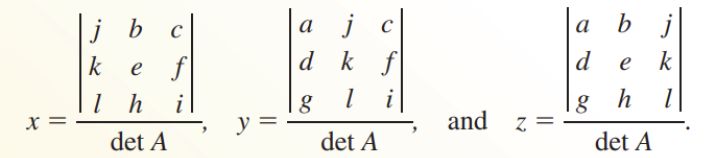
Lesson 4: Inverse Matrices

• Finding Inverse Matrices

  • The n x n identity matrix is a matrix with ones for all elements on the main diagonal (top left to bottom right) and zeros for all the other elements

  • If A is any n x n matrix and I is the n x n identity matrix, then AI = A and IA = A

  • 

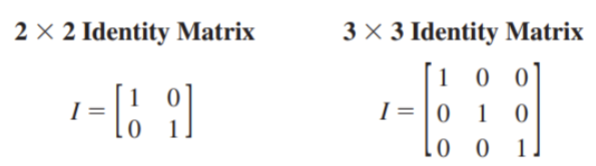
  • Two n x n matrices A and B are inverses of each other when their product is the n x n identity matrix; AB = I and BA = I

  • An n x n matrix A has an inverse if and only if det A ≠ 0

  • The inverse of A is denoted by A-1

• The Inverse of a 2x2 Matrix

  

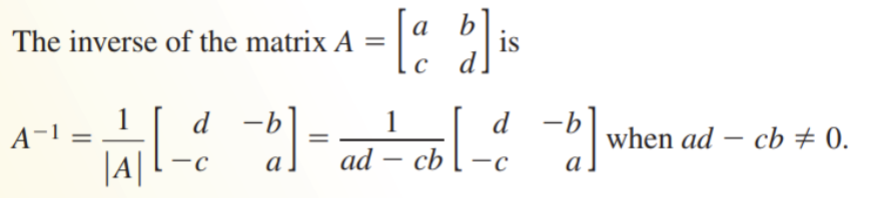
• Using an Inverse Matrix to Solve a Linear System

  • Write the system as a matrix equation AX = B; the matrix A is the coefficient matrix, X is the matrix of variables, and B is the matrix of constants

  • Find the inverse of matrix A

  • Multiply each side of AX = B by A-1 on the left to find the solution X = A-1B