Chapter 2 - Thermodynamics and Gases
Atomic Behavior
- The temperature of an object indicates the speed at which the molecules are vibrating
- Hot objects = higher speed
- Cold objects = slower speed
- Temperature is a direct measure of average kinetic energy
- In general, hot objects expand and cold objects shrink a little bit
- The motion of atoms follows a pattern that is shown in graphs of the number of atoms vs average kinetic energy as a normal curve
- Hot temperatures have a lower peak that’s shifted to the right but has the same area under the curve
- Cold temperatures have a higher peak that’s shifted to the left but has the same area under the curve
- This means that it’s possible for some cold atoms to have greater kinetic energy than hot atoms but on average, hot atoms have more kinetic energy
- Thermal energy moves from hot to cold
- This is because hot molecules tend to collide with cold molecules which result in a net transfer of kinetic energy to the cold molecule
- Remember, this is still on average - exceptions do occur
- For objects at the same temperature, there is still an energy exchange between them but the net transfer is 0
- We call this thermal equilibrium
Heat, Temperature, and Power
- Heat (Q) - a type of energy that can be transferred between objects
- Measured in Joules
- Heat vs. Internal Energy
- Heat is transferred not possessed - 10 J of heat was transferred to the second box
- Internal energy is possessed - The box has 10 J of internal energy
- Internal Energy (U): The sum of the energies of all molecules in a substance
- Temperature (T): Related to average kinetic energy
- Measured in Kelvins or Degrees Celsius
- @@Kelvin = Celsius + 273@@
- Two bodies at the same temperature don’t always have the same internal energy
- A bigger object of the same material and temperature will have more internal energy than a smaller object
- Power: Work per time
- Measured in Joules per second (same thing as Watts)
Heat Transfer
- There are 3 physical methods of heat transfer
Conduction: the transfer of energy from vibrations from atom to atom of an object from the hotter side to the colder side
In other words, when 2 objects are touching, the transfer of energy from the hot to the cold object until they’re in thermal equilibrium
Factors that can affect the rate of this heat transfer:
Thermal conductivity (k) of the material
- Metals are better conductors and have a higher thermal conductivity as compared to something like a piece of wood
The difference in temperatures of the two objects
- A greater temperature difference will cause a faster rate of heat transfer
The cross-sectional area of the object the heat is transferred through
- A larger cross-sectional area will cause a faster rate of heat transfer
The length of the material the heat is transferred through
- A longer object will cause a slower rate of heat transfer
These factors combine to form the equation for the rate of heat transfer:
==ΔQ/t = kAΔT/L==
- ΔQ/t = rate of heat transfer (J/s)
- k = thermal conductivity
- A = cross-sectional area (m^2)
- ΔT = temperature difference (K)
- L = length (m)
Convection: the transfer of thermal energy through fluid flow
- Because hotter objects expand, fluids are less dense and naturally rise because their volume is bigger but their mass is the same
Radiation: transfer of energy through electromagnetic waves
- The vibration of charged particles (protons and electrons) creates electromagnetic waves
- These waves carry energy away from the object
Kinetic Theory of Gases
- The Kinetic Theory of Gases assumes for ideal gases:
- Molecules move continuously and randomly
- There is a large number of gas molecules in a container
- Molecules don’t exert electrical or gravitational forces on each other
- All collisions between molecules are elastic
- In elastic collisions, kinetic energy is not lost
- The Kinetic Theory of Gases derives the following equations:
- ==U = 3/2 nRT = 3/2 NkT==
- U - internal energy
- R - Ideal gas constant - on equation sheet
- k - Boltzmann’s constant - given on the equation sheet
- T - temperature
- Relates the internal energy of a gas to its temperature
- ==v = sqrt((3kT)/(m))==
- v - velocity of a gas
- m - mass
- k - Boltzmann’s constant - given on the equation sheet
Ideal Gas Law
- PV = nRT
- P - pressure (Pascal - Newton per meter squared)
- V - volume of the gas (cubic meters)
- n - number of moles of gas
- R - ideal gas constant
- T - temperature (K)
- PV = NkT
- N - number of molecules
- k - Boltzmann’s constant - given on equation sheet
- In times when the number of moles are constant, PV/T is also held constant
- Use this formula for calculations
- Graphical Analysis
- When graphing pressure versus temperature, the temperature at which pressure is 0 is called absolute zero
- Zero volume of gas will occur at absolute zero if we plot volume as a function of temperature
First Law of Thermodynamics
- First Law of Thermodynamics: The internal energy of a system is conserved
- @@ΔU = Q + W@@
- ΔU - internal energy
- Q - heat added to the gas
- If heat is added, sign of Q is positive
- W - work done on the gas
- If the gas is compressed, work is done on the gas and W is positive
- If the gas is expanded, work is done by the gas and W is negative
- Remember that Work = Force x distance
PV Diagrams
PV Diagrams - graphs of pressure on the y-axis and volume on the x-axis
Isothermal lines - a line in which every point that has the same PV value (and therefore the same T)
@@Work = -PΔV@@
- Moving to the right on a PV graph is negative work and vice versa
- Area under the curve of the graph is equal to magnitude of work
To find ΔT, compare the PV path to isothermal lines or see if P or V changed
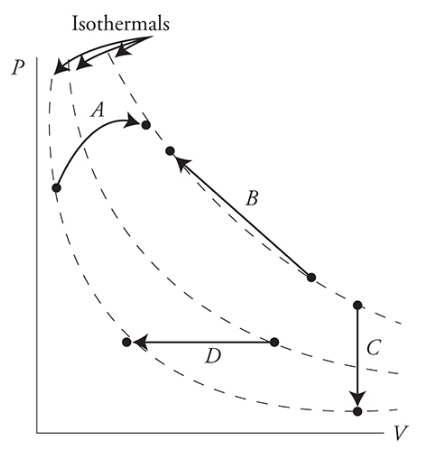
To find ΔU, find ΔT because ==ΔU = 3/2 nRΔT==
To find Q, use ΔU = Q + W where Q and W are already given or are found from area under the graph and/or ΔT
Cycles on a PV diagram
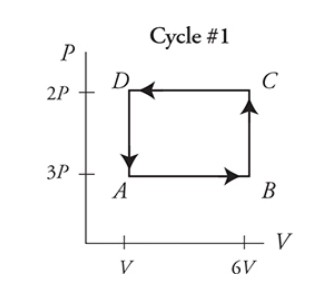
Cycles: paths on the PV diagram that start and end at the same point
Same PV value at the start and end → ΔT is 0 → ΔU is 0 → Q = -w (remember the first law of thermodynamics)
Work becomes the area contained in the shape created by the cycle
Four Special Processes (Paths)
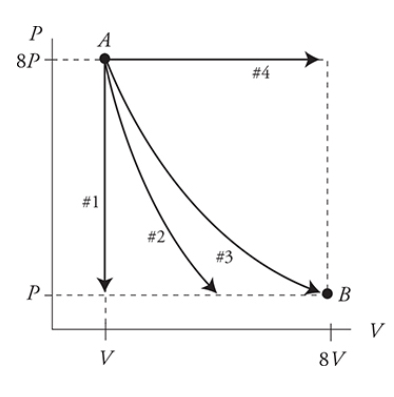

Constant Pressure - Isobaric
- Horizontal lines on the PV graph
Constant Volume - Isochoric (Isovolumetric)
- Vertical lines on PV graph
Constant Temperature - Isothermal
- Hyperbolic constant lines on the PV graph
- Less steep than Adiabatic processes
- ==Q = -W==
No Heat Transfer Between System and Environment - Adiabatic
- Curved path but steeper than Isothermal process
Entropy
- Entropy: a measure of disorder
- Second Law of Thermodynamics: The entropy of a system cannot decrease unless work is done on that system
- Think of a glass: when broken, work must be done to put it back together in a more orderly state
- The universe has a tendency towards entropy
- When heat flows into a system, entropy increases