Chapter 2 - Thermodynamics and Gases

Atomic Behavior

• The temperature of an object indicates the speed at which the molecules are vibrating
  • Hot objects = higher speed
  • Cold objects = slower speed
• Temperature is a direct measure of average kinetic energy
• In general, hot objects expand and cold objects shrink a little bit
• The motion of atoms follows a pattern that is shown in graphs of the number of atoms vs average kinetic energy as a normal curve
  • Hot temperatures have a lower peak that’s shifted to the right but has the same area under the curve
  • Cold temperatures have a higher peak that’s shifted to the left but has the same area under the curve
  • This means that it’s possible for some cold atoms to have greater kinetic energy than hot atoms but on average, hot atoms have more kinetic energy
  • Thermal energy moves from hot to cold
  • This is because hot molecules tend to collide with cold molecules which result in a net transfer of kinetic energy to the cold molecule
  • Remember, this is still on average - exceptions do occur
  • For objects at the same temperature, there is still an energy exchange between them but the net transfer is 0
  • We call this thermal equilibrium

Heat, Temperature, and Power

• Heat (Q) - a type of energy that can be transferred between objects
  • Measured in Joules
• Heat vs. Internal Energy
  • Heat is transferred not possessed - 10 J of heat was transferred to the second box
  • Internal energy is possessed - The box has 10 J of internal energy
  • Internal Energy (U): The sum of the energies of all molecules in a substance
• Temperature (T): Related to average kinetic energy
  • Measured in Kelvins or Degrees Celsius
  • @@Kelvin = Celsius + 273@@
  • Two bodies at the same temperature don’t always have the same internal energy
  • A bigger object of the same material and temperature will have more internal energy than a smaller object
• Power: Work per time
  • Measured in Joules per second (same thing as Watts)

Heat Transfer

• There are 3 physical methods of heat transfer

1. Conduction: the transfer of energy from vibrations from atom to atom of an object from the hotter side to the colder side

   1. In other words, when 2 objects are touching, the transfer of energy from the hot to the cold object until they’re in thermal equilibrium

   2. Factors that can affect the rate of this heat transfer:

      1. Thermal conductivity (k) of the material

         1. Metals are better conductors and have a higher thermal conductivity as compared to something like a piece of wood

      2. The difference in temperatures of the two objects

         1. A greater temperature difference will cause a faster rate of heat transfer

      3. The cross-sectional area of the object the heat is transferred through

         1. A larger cross-sectional area will cause a faster rate of heat transfer

      4. The length of the material the heat is transferred through

         1. A longer object will cause a slower rate of heat transfer

   3. These factors combine to form the equation for the rate of heat transfer:

      1. ==ΔQ/t = kAΔT/L==

         1. ΔQ/t = rate of heat transfer (J/s)
         2. k = thermal conductivity
         3. A = cross-sectional area (m^2)
         4. ΔT = temperature difference (K)
         5. L = length (m)

2. Convection: the transfer of thermal energy through fluid flow

   1. Because hotter objects expand, fluids are less dense and naturally rise because their volume is bigger but their mass is the same

3. Radiation: transfer of energy through electromagnetic waves

   1. The vibration of charged particles (protons and electrons) creates electromagnetic waves
   2. These waves carry energy away from the object

Kinetic Theory of Gases

• The Kinetic Theory of Gases assumes for ideal gases:
  • Molecules move continuously and randomly
  • There is a large number of gas molecules in a container
  • Molecules don’t exert electrical or gravitational forces on each other
  • All collisions between molecules are elastic
  • In elastic collisions, kinetic energy is not lost
• The Kinetic Theory of Gases derives the following equations:
  • ==U = 3/2 nRT = 3/2 NkT==
  • U - internal energy
  • R - Ideal gas constant - on equation sheet
  • k - Boltzmann’s constant - given on the equation sheet
  • T - temperature
  • Relates the internal energy of a gas to its temperature
  • ==v = sqrt((3kT)/(m))==
  • v - velocity of a gas
  • m - mass
  • k - Boltzmann’s constant - given on the equation sheet

Ideal Gas Law

• PV = nRT
  • P - pressure (Pascal - Newton per meter squared)
  • V - volume of the gas (cubic meters)
  • n - number of moles of gas
  • R - ideal gas constant
  • T - temperature (K)
• PV = NkT
  • N - number of molecules
  • k - Boltzmann’s constant - given on equation sheet
• In times when the number of moles are constant, PV/T is also held constant
  • Use this formula for calculations
• Graphical Analysis
  • When graphing pressure versus temperature, the temperature at which pressure is 0 is called absolute zero
  • Zero volume of gas will occur at absolute zero if we plot volume as a function of temperature

First Law of Thermodynamics

• First Law of Thermodynamics: The internal energy of a system is conserved
• @@ΔU = Q + W@@
  • ΔU - internal energy
  • Q - heat added to the gas
  • If heat is added, sign of Q is positive
  • W - work done on the gas
  • If the gas is compressed, work is done on the gas and W is positive
  • If the gas is expanded, work is done by the gas and W is negative
  • Remember that Work = Force x distance

PV Diagrams

• PV Diagrams - graphs of pressure on the y-axis and volume on the x-axis

• Isothermal lines - a line in which every point that has the same PV value (and therefore the same T)

• @@Work = -PΔV@@

  • Moving to the right on a PV graph is negative work and vice versa
  • Area under the curve of the graph is equal to magnitude of work

• To find ΔT, compare the PV path to isothermal lines or see if P or V changed

  

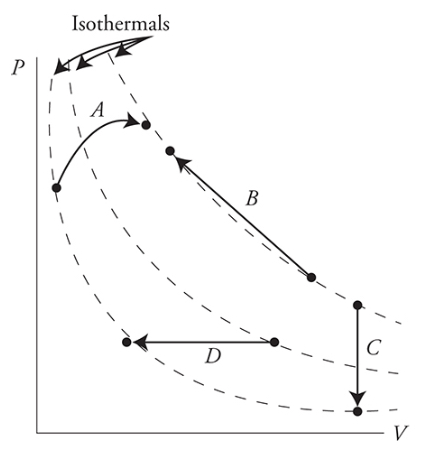
• To find ΔU, find ΔT because ==ΔU = 3/2 nRΔT==

• To find Q, use ΔU = Q + W where Q and W are already given or are found from area under the graph and/or ΔT

• Cycles on a PV diagram

  

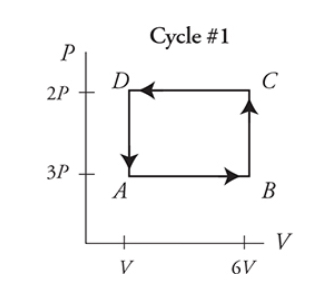
  • Cycles: paths on the PV diagram that start and end at the same point

  • Same PV value at the start and end → ΔT is 0 → ΔU is 0 → Q = -w (remember the first law of thermodynamics)

  • Work becomes the area contained in the shape created by the cycle

  • Four Special Processes (Paths)

    

    

  \

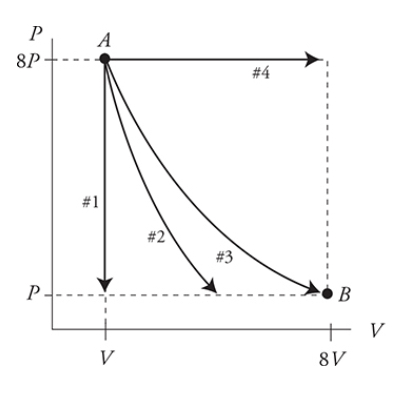
  • Constant Pressure - Isobaric
    • Horizontal lines on the PV graph
  • Constant Volume - Isochoric (Isovolumetric)
    • Vertical lines on PV graph
  • Constant Temperature - Isothermal
    • Hyperbolic constant lines on the PV graph
    • Less steep than Adiabatic processes
    • ==Q = -W==
  • No Heat Transfer Between System and Environment - Adiabatic
    • Curved path but steeper than Isothermal process

Entropy

• Entropy: a measure of disorder
• Second Law of Thermodynamics: The entropy of a system cannot decrease unless work is done on that system
  • Think of a glass: when broken, work must be done to put it back together in a more orderly state
• The universe has a tendency towards entropy
• When heat flows into a system, entropy increases

\