SEM Modellspezifikation

SEM = structural equation models (=Strukturgleichungsmodelle)

werden verwendet, um Theorien zu überprüfen oder zu entwickeln

Vorteile: Theorien lassen sich umfassend überprüfen, Konstrukte und ihre Indikatoren werden explizit getrennt, Messfehler werden explizit berücksichtigt

1. Schritt: Theorie in ein Pfaddiagramm übertragen (enthält alle theorierelevanten Konstrukte, die zur Messung verwendeten Indikatoren (z.B. Testwerte), und Verknüpfungen zwischen den Konstrukten, sowie zwischen Konstrukten und Idikatoren)

Begriffe:

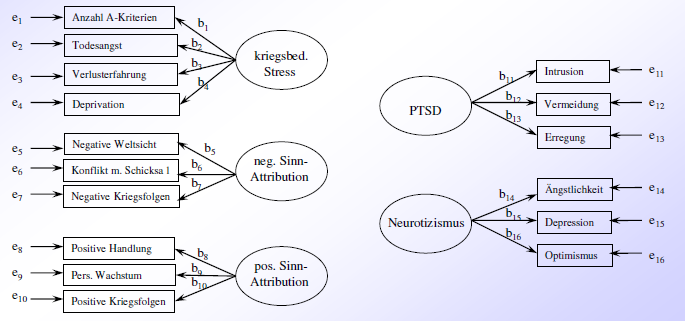
• Messmodell: beschreibt die Verknüpfung zwischen einer latenten Variable und ihren Indikatoren (manifeste Variablen)

→ spezifiziert die Operationalisierung des Konstrukts

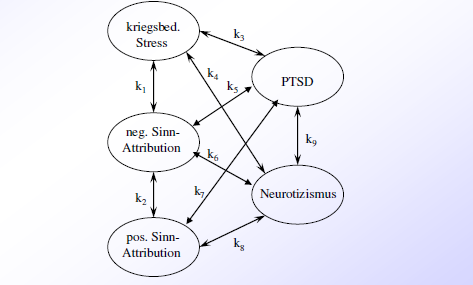
• Strukturmodell: beschreibt die Verknüpfung zwischen latenten Variablen, oder zwischen latenten Variablen und manifesten Variablen, welche nicht als Indikatoren für latente Variablen verwendet werden

Beispiel:

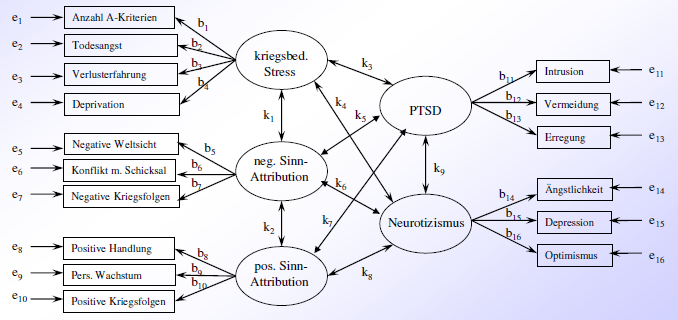
• manifeste Variable: beobachtete Variable (Messergebnis) → graphisch: Kästchen

• latente Variable: nicht beobachtete/theoretisch angenomme Variable (Konstrukt) → graphisch: Kreise

• Residuum: durch kein Konstrukt erklärter Anteil einer einzelnen Variable → graphisch: meist nicht umrandet, nur ein Pfeil

• endogene Variable (abhängige Variablen): Variable, die durch andere Varibalen erklärt wird (die meisten manifesten Variblen, manche latenten Variablen) → graphisch: mehrere Pfeile zeigen auf die endogene Variable

• exogene Variable (unabhängige Variablen): Variable, die nicht durch andere Variablen erklärt wird (beinhaltet alle Residuen, manche latente Variablen und manche manifeste Variablen) → graphisch: kein Pfeil zeigt auf die exogene Variable

• Pfad: Verbindung zwischen zwei Variablen

  Varianten:

  • gerichteter Zusammenhang → graphisch: einfacher Pfeil; numerisch: Regressionsgewicht)

  • ungerichteter Zusammenhang → graphisch: Doppelpfeil; numerisch: Kovarianz/Korrelation

• Pfadkoeffizient: Stärke eines gerichteten Zusammenhangs = Regressionsgewicht (synonym: Ladung, Gewicht)

• (Modell-)Parameter: alle latenten Variablen, Pfadkoeffizienten und latenten Kovarianzen

  • fixierte Parameter: werden a priori auf einen Wert festgelegt (für Pfade meist null oder eins)

  • freie Parameter: werden anhand der empirischen Daten geschätzt

  • eingeschränkte Parameter: müssen numerischen Bedingungen genügen

Arten von Messmodellen:

Modell essentiell tau-äquivalenter Variablen: Alle Pfadkoeffizienten vom Konstrukt auf seine Indikatoren sind auf eins fixiert

Modell tau-kongenerischer Variablen: Die Pfadkoeffizienten vom Konstrukt zu seinen Indikatoren können unterschiedliche Werte annehmen

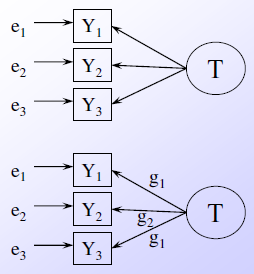
Modellidentifikation: Berechnung/Schätzung der freien Parameter anhand der empirischen Daten → Verhältnis zwischen unbekannten Variablen (freie/eingeschränkte Parameter) und bekannten Variablen (Stichprobenmomente)

→ exakte Identifikation: wenn jeder unbekannte Parameter auf nur eine einzige Weise aus den Daten berechnet werden kann (df=0)

→ Überidentifikation: wenn unbekannte Parameter auf unterschiedlieche Weisen aus den Daten berechnet werden können (df>0)

→ Unteridentifikation: wenn wenigstens ein unbekannter Parameter auf keine Weise aus den Daten berechnet werden kann (df<0)

Definitionsgleichungen

• geben algebraisch an, wie sich jede endogene Variable aus exogenen Variablen zusammensetzt, und wie die exogenen Variablen zusammenhängen

  → Zerlegung von endogenen Variablen in exogene Variablen (gewichtete Summen)

  → Zusammenhang der exogenen Variablen (Korrelationen)

Hinweis: ein Pfeil ohne expliziten Pfadkoeffizient heißt (in der Vorlesung) immer, dass der Pfadkoeffizient auf 1 fixiert wurde; und wenn zwischen zwei exogenen Variablen kein Doppelpfeil steht, bedeutet das immer, dass die Kovarianz zwischen den beiden Variablen auf 0 fixiert wurde (also unkorreliert laut Modell)

Problem der Identifizierbarkeit 1

ein Gleichungssystem ist nur dann lösbar, wenn mindestens so viele bekannte Größen wie unbekannte Größen vorhanden sind (notwendiges Kriterium)

zum Beispiel: x+y = 10 ist nicht lösbar

→ das System der Definitionsgleichungen ist für eine Person nicht lösbar (man hätte dann nur Werte für die manifesten Variablen, aber kann die latenten Variablenwerte der Person nicht identifizieren

Lösung: man analysiert die Daten von mehreren Personen und arbeitet mit den Varianzen (Varianzen der latenten Variablen sind für eine Stichprobe identifizierbar)

→ Modell der manifesten/latenten Variablen wird zu Modell der Varianzen und Kovarianzen von manifesten/latenten Variablen (Kovarianzstrukturmodell und Kovarianzstrukturanalyse)

Rechnen mit Varianzen und Kovarianzen

Definitionen:

Die Varianz gibt an, wie stark die einzelnen Werte einer Verteilung im Durchschnitt vom Mittelwert abweichen
Dazu berechnet man die Abweichung jedes Wertes vom Mittelwert, quadriert diese Abweichungen (damit negative Abweichungen nicht wegfallen), summiert sie und teilt das Ergebnis durch die Anzahl der Werte.

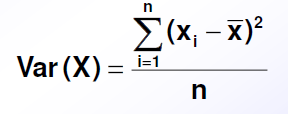
Die Kovarianz misst, wie zwei Variablen gemeinsam vom jeweiligen Mittelwert abweichen.
Man schaut sich an, wie stark jeder Wert von X und gleichzeitig der zugehörige Wert von Y vom jeweiligen Mittelwert abweicht. Diese Abweichungen werden miteinander multipliziert, alle Produkte aufsummiert und durch die Anzahl der Werte geteilt.

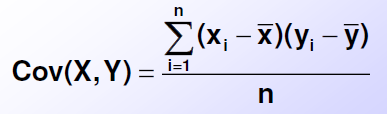
DIE RECHENREGELN

Rechenregel 1:

gegeben sei eine Zufallsvariable X, dann gilt:

Cov(X,X) = Var (X)

Rechenregel 2:

gegeben seien zwei Linearkombinationen aX + bY und cV + dW, welche sich aus den Zufallsvariablen X,Y,V,W und den Konstanten a,b,c,d zusammensetzen.

Dann gilt:

Cov(aX + bY, cV + dW)=

ac*Cov(X,V) + ad*Cov(X,W) + bc*Cov(Y,V) + bd*Cov(Y,W)

Rechenregel 3:

gegeben sei eine Linearkombination aX + bY, welche sich aus den Zufallsvariablen X und Y sowie den Konstanten a und b zusammensetzen. Dann gilt:

Var (aX + bY) = a²Var (X) + b²Var (Y) + 2ab * Cov(X,Y)

—> können genutzt werden, um die Definitionsgleichungen in Strukturgleichungen zu überführen

Strukturgleichungen

beschreiben statistisch, wie alle Varianzen/Kovarianzen der endogenen Variablen durch Variationen in den exogenen Variablen bedingt werden

dabei geht das ursprüngliche Modell der manifesten/latenten Variablen in ein Modell der Varianzen/Kovarianzen der manifesten/latenten Variablen über (“Strukturgleichungsmodell”)

Aufgabe des Strukturgleichungsmodells: die Kovarianzstruktur der manifesten Variablen zu erklären

Kovarianzstruktur = Größenverhältnis aller Varianzen/Kovarianzen der manifesten Variablen

→ das Strukturgleichungsmodell erlaubt eine Zerlegung der beobachteten Varianzen/Kovarianzen in hypothetische Varianzquellen

Hinweis: die Pfaddiagramme bleiben gleich, auch wenn jetzt im Strukturgleichungsmodell nicht die latenten Variablen geschätzt werden, sondern deren Varianzen

Problem der Identifizierbarkeit 2

Die Überführung der Definitionsgleichungen in Strukturgleichungen führt schon in manchen Fällen zu Identifizierbarkeit (also mehr Bekannte als Unbekannte)

ABER nicht immer

weiteres Identifikationsproblem: wenn im Modell alle wegführenden Pfeile von einer freien latenten Variable frei sind, also nicht fixiert (selbst wenn im gesamten Modell die Anzahl der bekannten Größen größer ist als die Anzahl der Unbekannten)

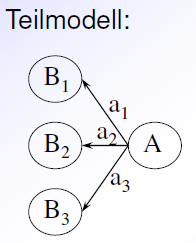
Lösungsmöglichkeiten:

Normierung von Pfaden: wenigstens ein Pfadkoeffizient wird auf 1 fixiert

Standardisierung von Varianzen: die Varianz einer latenten Variable wird auf 1 fixiert

Identifizierbarkeit ist nur dann gegeben, wenn:

• die Anzahl aller unbekannten Größen kleiner/gleich der Anzahl aller bekannten Größen ist (notwendig aber nicht hinreichend)

• UND bei keiner freien latenten Variable alle wegführenden Pfade frei sind

Modellspezifikation

= der Prozess, der eine Theorie in ein Modell überführt (Modell: formale Beschreibung der Theorie inkl. Pfaddiagramm und Definitionsgleichungen)

• die Theorie definiert die Konstrukte und ihre Zusammenhänge (→ Strukturmodell)

• Hilfstheorien definieren die Messung der Konstrukte (→ Messmodell)

Worauf man bei der Modellspezifikation achten sollte (um es identifizierbar zu halten):

• nur wenige Konstrukte

• viele Indikatoren

• mindestens so viele bekannte wie unbekannte Parameter

• Teilmodelle durch Normierung/Standartisierung identifizierbar machen

• Restriktion (zum Beispiel gleichsetzung von Varianzen von Residuen) können helfen

• Einfachheitskriterium (wenige unbekannte)

(Identifizierbarkeitsdiagnose auch durch Software möglich)

Identifikationsgleichungen

geben an, wie sich die unbekannten latenten Parameter (Varianzen/Kovarianzen von latenten Variablen und Pfadkoeffizienten) aus den beobachtbaren Größen berechnen lassen

→ Umformung der Strukturgleichungen

Identifikationsgleichungen erlauben auch eine Diagnostik der Identifizierbarkeit

• für mindestens einen Parameter keine Identifikationsgleichung möglich → unteridentifiziert

• für jeden Parameter genau eine Identifikationsgleichung → genau identifiziert

• für mindestens einen Parameter mehr als eine Identifikationsgleichung möglich → überidentifiziert

!!! nur überidentifizierte Modelle sind testbar !!!