Chapter 1: Introduction and Mathematical Concepts
1.1: The Nature of Physics
- ==Physics== is the study of our physical environment: the structure of matter and how these structures interact with each other.
- Many objects, items, and products were designed based on physics.
- In fact, many industries rely on such products.
- Other industries were birthed from the concepts of physics.
- Because physics is so fundamental, it is a required course for many majors.
1.2: Units
- In AP physics courses, students are expected to use ==SI units== (International System of Units).
- The first three are the main base units for AP Physics 1.
- ==Base units== are used alongside various laws to define additional units.
- The additional units are called ==derived units== because they are derived from the base units.
| Measurement | Unit |
|---|---|
| Length | Meter (m) |
| Mass | Kilogram (kg) |
| Time | Seconds (s) |
| Frequency | Hertz (Hz) |
| Velocity | Meters per seconds (m/s) |
| Acceleration | Meters per seconds squared (m/s²) |
| Force | Newtons (N) |
| Momentum | Newton seconds (N s) |
| Inertia | Kilogram meters squared (kg m²) |
| Energy | Joules (J) |
| Power | Watt (W) |
| Angle | Radian (rad) |
| Angular velocity or frequency | Radians per second (rad/s) |
| Angular acceleration | Radians per second squared (rad/s²) |
1.3: The Role of Units in Problem Solving
The Conversion of Units
Since any quantity can be measured in several units, you need to know how to convert from one unit to another.
- Explicitly write your current value and units (in fraction form)
- Multiply your expression by a converting ratio that is equivalent to 1.
- Repeat step 2 until you reach your desired units.
Example:

During a conversion, if the units do not reach the desired result, the conversion has not been carried out properly.
Only quantities with the same units can be added or subtracted.
Dimensional Analysis
- ==Dimension==: the physical nature of a quantity and the type of unit used to specify it
- ==Dimensional analysis== is used to check mathematical relations for consistency.
- Example: let the dimension of x = L, and t = T. Note that v = x/t = L/T
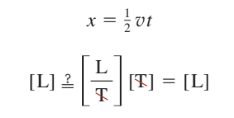
1.4: Trigonometry
- ==Trigonometry== is the study of relationships between the lengths and angles of a triangle.
- Physics often utilizes trigonometry due to the nature of vectors.
- The three main trigonometric functions are sine, cosine, and tangent.
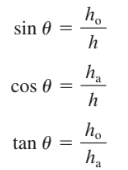
- Vice versa, the three main inverse trigonometric functions are
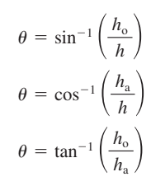
- For right triangles, the Pythagorean theorem can be used to solve a missing side.

1.5: Scalars and Vectors
- A ==scalar== quantity has only magnitude (how much of something).
- A ==vector== quantity has both magnitude and direction.
- In drawings, the length of an arrow is proportional to the magnitude of a vector and the direction of an arrow gives the direction of a vector.
- In writing, the angle gives the direction of a vector.
- Vectors are often denoted by arrows above the variable or are bold faced.
1.6: Vector Addition and Subtraction
Addition
- The total vector (sum or difference of two vectors) is often called the ==resultant vector==.
- You can only simply add vectors if they are in the same direction.
- If not, you must find the magnitude and angle separately.
- For right triangles, use the Pythagorean theorem to find the hypotenuse which will be the magnitude of the resultant vector. Then use the tangent inverse to find the angle.
- For non-right triangles, you can either use a graphical method (compare lengths of vectors) or break them down into components (discussed in next section).
Subtraction
- When a vector is multiplied by -1, its magnitude remains the same, but the direction of the vector is reversed.
- Vector subtraction is carried out exactly like vector addition, except one vector is multiplied by -1.
1.7: The Components of a Vector
Vector Components
Any vector can be expressed in terms of its vertical and horizontal parts called ==vector components==.
For example, A can be expressed as the sum of Aₓ and Aᵧ
In other words, A = Aₓ + Aᵧ
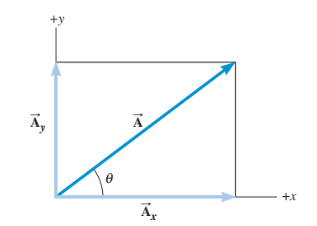
Scalar Components
==Scalar components== are the magnitudes of a vector’s components.
==Unit vectors== are vectors of magnitude 1 without dimensions (units)
Together, they can describe two separate vector components that make up a resultant vector.
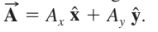
Resolving a Vector into Its Components
- The equation A = Aₓ + Aᵧ can be expanded using trigonometry to solve for the side lengths.
- A = Aₓ + Aᵧ = A cosθ + A sinθ
- Aₓ = A cosθ
- Aᵧ = A sinθ
1.8: Addition of Vectors by Means of Components
Two vectors can be individually split into their horizontal and vertical components.
Then, the two horizontal components can be added together and the two vertical components can be added together to form a right triangle.
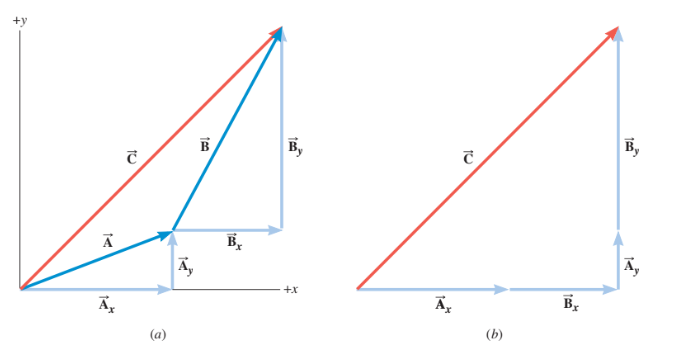
This makes solving the resultant much easier because you can use the Pythagorean theorem to find the magnitude and an inverse trigonometric function to find the angle.