Plane Kinetics of Rigid Bodies

• Kinetics of Rigid Bodies: Deals with the relationships between external forces on a body and its resulting translational and rotational motions.

• Plane Motion: Motion of a body approximated as a thin slab confined to a plane, which contains the mass center, with forces projected onto this plane. Symmetrical bodies with appreciable dimensions normal to the plane can also be considered in plane motion.

• To define the plane motion of a rigid body, two force equations and one moment equation (or equivalent) are needed.

• Isolate the body or system to be analyzed using a free-body diagram to define it explicitly.

• All external forces acting on the body or system should be identified after defining the complete external boundary.

• The mass moment of inertia accounts for the radial mass distribution relative to a rotation axis and is crucial for solving rotational problems. Refer to Appendix B for calculation details.

General Equations of Motion

• Force Equation: \Sigma\overline{F}=m\overline{a} (Eq. 4/1)

  • The resultant of external forces (\Sigma F) equals the body's mass (m) times the acceleration (a) of its mass center (G).

• Moment Equation: \Sigma\overline{M}_{G}=\dot{\overline{H}}_{G} (Eq. 4/9)

  • The resultant moment about the mass center (\Sigma M_G ) equals the time rate of change of angular momentum about the mass center.

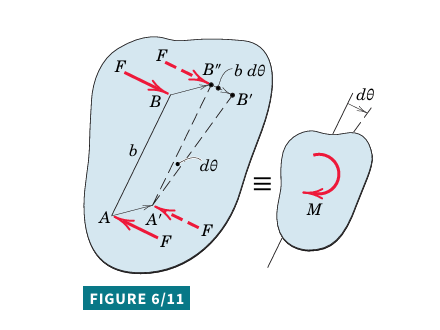
• A general force system on a rigid body can be simplified into a resultant force at a chosen point and a corresponding couple.

• By placing the resultant force through the mass center, you can better visualize force action and body response.

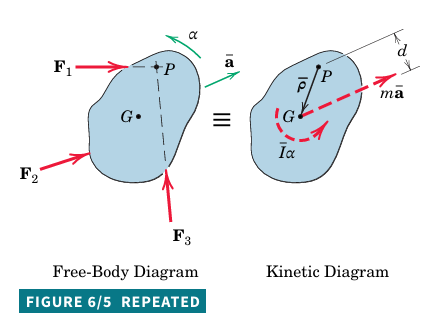
• Free-body diagram: illustrates external forces acting on the body.

• Kinetic diagram: Represents dynamic effects using Eqs. 4/1 and 4/9.

• The equivalence between these diagrams helps visualize translational and rotational effects.

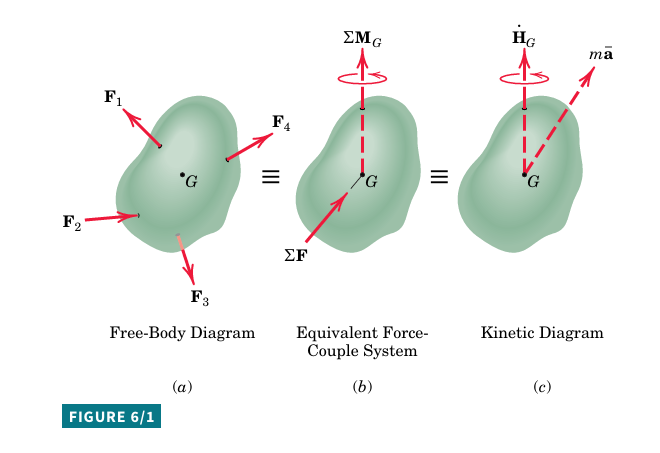
Plane-Motion Equations

• For plane motion in the x-y plane:

  • Angular velocity: \overline{\omega}=\omega k.

  • Angular acceleration: \overline{\alpha}=\alpha k , both positive in the z-direction.

  • Use scalar notation (\omega and \alpha = \dot{\omega} ) because the z-direction of \omega and \alpha is perpendicular to the plane of motion.

• Angular momentum about the mass center: \overline{H}_{G}=\Sigma\overline{\rho}_{i}\times m_{i}\dot{\overline{\rho}}_{i} , where \overline{\rho}_{i} is the position relative to G of the representative particle of mass m_{i}.

  • For a rigid body, the velocity of m_{i} relative to G is \dot{\overline{\rho}}_{i}=\overline{\omega}\times\overline{\rho}_{i}.

  • The magnitude of \overline{H}_{G} becomes H_{G}=\Sigma\rho_{i}^2m_{i}\omega=\omega\Sigma\rho_{i}^2m_{i}.

  • The summation \int\rho^2dm is the mass moment of inertia I about the z-axis through G.

  • H_{G}=\overline{I}\omega where \overline{I} is a constant property representing rotational inertia.

• The moment equation becomes \Sigma M_{G}=\dot{H_{G}}=\overline{I}\dot{\omega}=\overline{I}\alpha where \alpha=\dot{\omega} is the angular acceleration of the body.

• General equations of motion for a rigid body in plane motion:

  • \Sigma\overline{F}=m\overline{a} (6/1)

  • \Sigma M_{G}=\overline{I}\alpha

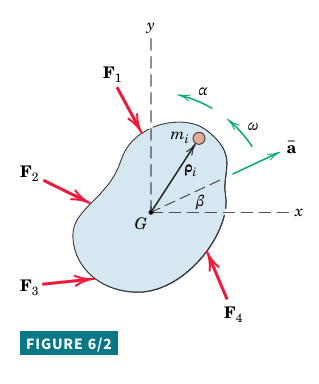
Alternative Moment Equations

• General equation for moments about an arbitrary point P (Eq. 4/11):

  • \Sigma\overline{M}_{P}=\dot{\overline{{H}}}_{G}+\overline{\rho}\times m\overline{a}

  • \overline{\rho} is the vector from P to the mass center G, and \overline{a} is the mass-center acceleration.

• For rigid-body plane motion, \dot{\overline{{H}}}_{G} becomes \overline{I}\alpha and \overline{\rho}\times m\overline{a} is the moment (m\overline{a}d) of m\overline{a} about P.

• For a two-dimensional body: \Sigma M_{P}=\overline{I}\alpha+m\overline{a}d (6/2)

  • All terms are positive in the counterclockwise sense in the given example.

• Alternative moment equation about P (Eq. 4/13):

  • \Sigma\overline{M}_{P}=(\dot{\overline{{H}}}_{P})_{rel}+\overline{\rho}\times m\overline{a}_{P}

  • If P is fixed to the body, (\dot{\overline{{H}}}_{P})_{rel} becomes I_{P}\alpha, where I_{P} is the mass moment of inertia about an axis through P and \alpha is the angular acceleration of the body.

  • So, \Sigma\overline{M}_{P}=I_{P}\overline{\alpha}+\overline{\rho}\times m\overline{a}_{P} (6/3)

  • When \overline{\rho}=0 , P is the mass center G, and \Sigma M_{G}=\overline{I}\alpha .

  • When P is a nonaccelerating point O fixed to the body, \overline{a}_{p}=0 , and \Sigma M_{o}=I_{O}\alpha (6/4).

  • Equation 6/4 applies to rotation about a nonaccelerating point O fixed to the body and simplifies Eq. 4/7.

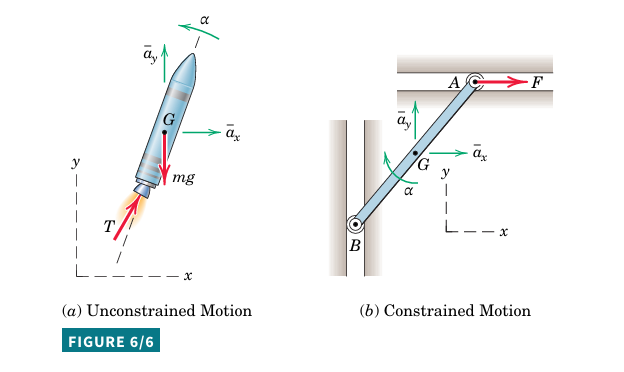
Unconstrained and Constrained Motion

• Unconstrained Motion: No physical constraints (e.g., rocket in vertical plane).

  • Acceleration components (\overline{a}_{x} , \overline{a}_{y} ) and angular acceleration \alpha are independent.

• Constrained Motion: Motion is physically confined (e.g., bar with guided ends).

  • Kinematic relationships between acceleration components and angular acceleration exist.

  • Requires kinematic analysis to relate linear and angular acceleration before solving force and moment equations.

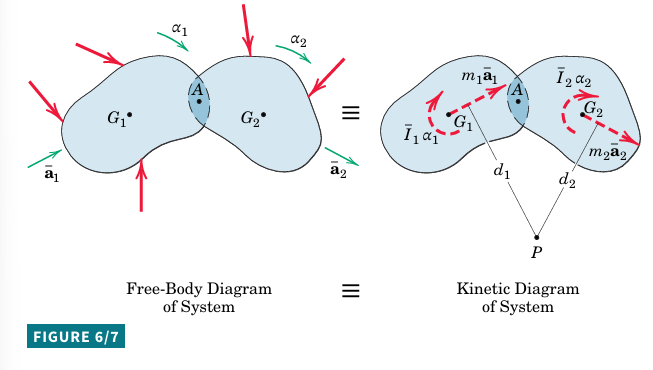
Systems of Interconnected Bodies

• For interconnected bodies with kinematically related motions, analyze the bodies as a system.

• Forces at connections are internal and not considered.

• \Sigma\overline{F}=\Sigma m\overline{a} (6/5)

• \Sigma M_{P}=\Sigma\overline{I}\alpha+\Sigma m\overline{a}d

• \\Sigma M_P = \Sigma I \alpha + \Sigma mad

  Summations represent terms for each separate body.

• If the system has more than three unknowns, dismember it and analyze each part separately.

  

Analysis Procedure

• 1. Kinematics:

  • Identify the type of motion.

  • Solve for linear and angular accelerations using kinematic information.

  • For constrained motion, relate linear acceleration to angular acceleration using relative-velocity and relative-acceleration equations.

• 2. Diagrams:

  • Draw a complete free-body diagram, assigning a coordinate system and labeling quantities.

  • Construct a kinetic diagram to clarify the equivalence between forces and dynamic response.

• 3. Equations of Motion:

  • Apply motion equations from Eqs. 6/1.

  • Use Eq. 6/2 or 6/3 as an alternative moment equation.

  • Combine with kinematic analysis results.

  • Ensure the number of independent equations equals the number of unknowns.

  • For solvable plane motion, there can be no more than five scalar unknowns determined from three motion equations and two relative-acceleration component relations.

Translation

• In translation, all lines in a moving body remain parallel to their original positions.

• Rectilinear Translation: Points move in straight lines.

• Curvilinear Translation: Points move on congruent curved paths (curved paths that are identical in shape and size).

• No angular motion occurs, so \omega and \alpha are zero.

• Moment of inertia is irrelevant for a translating body.

• Equations:

  • \Sigma\overline{F}=m\overline{a} (6/6)

  • \Sigma M_{G}=\overline{I}\alpha=0

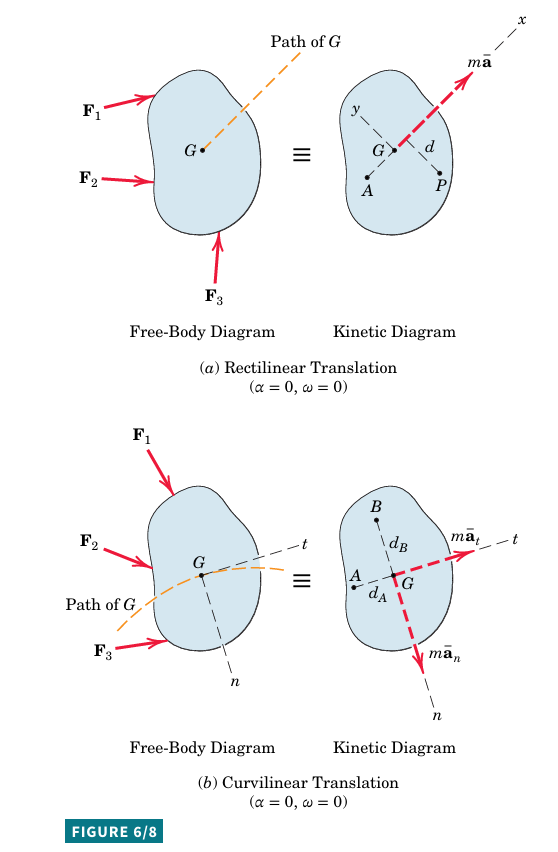
• For rectilinear translation with the x-axis in the acceleration direction, \Sigma\overline{F}x=m\overline{a}_{x} and \Sigma\overline{F}y=m\overline{a}_{y}=0.

• For curvilinear translation using n-t coordinates, \Sigma{\overline{F}{}_{n}}=m\overline{a}_{n} and \Sigma\overline{F}_{t}=m\overline{a}_{t}.

• In both cases, \Sigma M_G = 0.

• Alternative moment equation (Eq. 6/2) can be used.

• For rectilinear translation, \Sigma M_{P}=m\overline{a}d and \Sigma M_{a}=0.

• For curvilinear translation, \Sigma M_{A}=m\overline{a}_{n}d_{A} and \Sigma M_{B}=m\overline{a}_{t}d_{B}.

Fixed-Axis Rotation

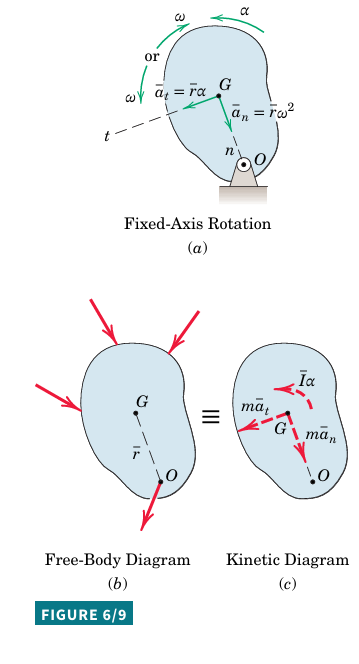
• Points in the body describe circles around the rotation axis.

• All lines in the plane of motion have the same \omega and \alpha.

• Mass center acceleration components are easily expressed in n-t coordinates: \overline{a}_{n}=\overline{r}\omega^2 and \overline{a}_{t}=\overline{r}\alpha.

• General equations for plane motion:

  • \Sigma\overline{F}=m\overline{a}

  • \Sigma M_{G}=\overline{I}\alpha

• Scalar components: \Sigma\overline{F}_{n}=m\overline{r}\omega^2 and \Sigma\overline{F}_{t}=m\overline{r}\alpha.

• Applying the moment equation about G requires accounting for the force applied at O.

• Direct moment equation about the rotation axis O:

  • \Sigma M_{o}=I_{o}\alpha (6/4)

• For rotation about the mass center G, a = 0, thus \Sigma F = 0, and the resultant of forces is the couple I \alpha.

General Plane Motion

• Combines translation and rotation.

• Equations:

  • \Sigma\overline{F}=m\overline{a}

  • \Sigma M_{G}=\overline{I}\alpha

Solving Plane-Motion Problems:

• Choice of Coordinate System: Use the system that best describes the mass center's acceleration (rectangular, normal-tangential, polar).

• Choice of Moment Equation: Use the alternative relation for moments about any point P, Eq. 6/2: \Sigma M_{P}=\overline{I}\alpha+m\overline{a}d

  • Consider using Eq. 6/3 when moments are about a point P with a known acceleration \Sigma\overline{M}_{P}=I_{P}\overline{\alpha}+\overline{\rho}\times m\overline{a}_{P}.

• Nonaccelerating point O on the body use the following equation: \Sigma M_{o}=I_{O}\alpha.

• Constrained versus Unconstrained Motion:

  • Constrained kinematic relationship between linear and angular accelerations and incorporate it into our force and moment equations of motion.

  • Unconstrained accelerations can be determined independently of one another by direct application of the three motion equations, Eqs. 6 ∕1.

• Number of Unknowns:

  • Check that total number of unknowns is less than or equal to number of equations which can be derived. For plane motion we have three scalar equations of motion and two scalar components of the vector relative-acceleration equation for constrained motion.

• Identification of the Body or System:

  • Emphasize the importance of clearly choosing the body to be isolated and representing this isolation by a correct free-body diagram.

• Kinematics:

  • Thorough review of the relative-acceleration relations for plane motion will be most helpful.

• Consistency of Assumptions:

  • Assumptions must be consistent with the principle of action and reaction any kinematic requirements

Work-Energy Relations

• Work of Forces and Couples:

  • U=\int\overline{F}\cdot d\overline{r}

  • U = \int (F \cos \alpha) ds