Chapter 4: Energy 

Work:

  • Work is defined as the transfer of energy when a force is applied to an object and causes it to move.
  • The unit of work is the joule (J), which is defined as the work done when a force of one newton is applied to an object and moves it through a distance of one meter.
  • Work can be positive, negative, or zero, depending on the direction of the force and the displacement of the object.
  • Work can be calculated using the formula: W = F x d x cos(theta), where F is the force applied, d is the distance moved, and theta is the angle between the force and the displacement vectors.

  \

 

  • Work can also be calculated as the change in kinetic energy of an object, using the work-energy theorem.
  • Work done by a conservative force, such as gravity, depends only on the initial and final positions of the object and is independent of the path taken.
  • Work done by a non-conservative force, such as friction, depends on the path taken and can result in a loss of mechanical energy.
  • The principle of work-energy conservation states that the total work done on an object is equal to the change in its kinetic and potential energy.

  \

Sample Problem 2

Calculate the total work (or net work) done on object M by the four forces indicated.

 

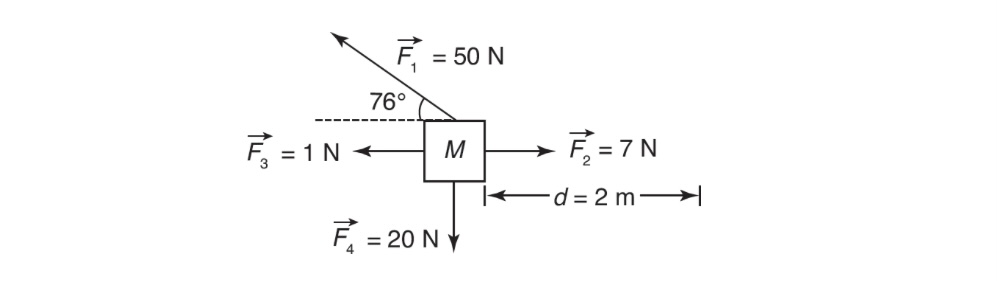
Solution

Total, or net, work is the sum of the individual works done by each of the individual forces.

Power:

  • Power is the rate at which work is done or energy is transferred.
  • The unit of power is watt (W), which is defined as one joule of work done per second.
  • Power can be calculated using the formula: P = W/t, where W is the work done and t is the time taken.
  • Power is a scalar quantity and can be positive, negative, or zero, depending on the direction of the work done and the time taken.
  • Power is important in many practical applications, such as engines, motors, and generators.

TIP:

When a constant force Fis applied to an object moving at constant velocity v, the power P is the product of the two values: P= Fiv.

 

 Dimensional analysis of the units of work and power. It is an important skill to be able to rewrite any defined unit in terms of the fundamental units of meters, kilograms, seconds, and coulombs.

Kinetic Energy and the Work-Energy Theorem:

  • Kinetic energy is the energy possessed by an object due to its motion.
  • The formula for kinetic energy is KE = 0.5 x m x v^2, where m is the mass of the object and v is its velocity.

  \

 

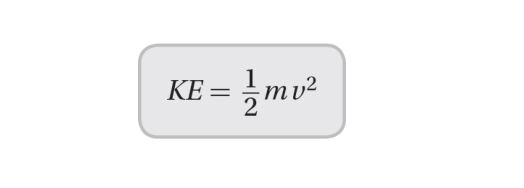
  • The work-energy theorem states that the net work done on an object is equal to its change in kinetic energy.
  • The work-energy theorem can be written as Wnet = KEf - KEi, where Wnet is the net work done, KEf is the final kinetic energy, and KEi is the initial kinetic energy.

Potential Energy and Conservative Forces:

  • Potential energy is the energy possessed by an object due to its position or configuration in a conservative force field.
  • Conservative forces are forces that do not dissipate energy and do not depend on the path taken by the object. Examples include gravitational and elastic forces.
  • The potential energy associated with a conservative force can be calculated using the formula: PE = -Wc, where Wc is the work done by the conservative force and PE is the potential energy.

 

 

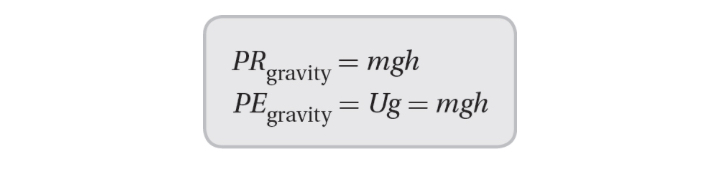
  • The potential energy can also be calculated as the negative of the work done by an external force to move the object from a reference position to its current position.
  • The total mechanical energy of an object in a conservative force field is the sum of its kinetic and potential energy and remains constant as the object moves within the force field.
  • The law of conservation of energy states that the total energy of a closed system, including all forms of energy (kinetic, potential, thermal, etc.), remains constant over time.

  \

Sample Problem

An arrow is shot from the roof of a building 30 meters high at 5 m/s and at an angle of 45 degrees. How fast will the arrow be going when it hits the ground?

Solution

From the information given, we know that:

\  

Sample Problem 8

A 2-kg mass sliding along a frictionless floor at 3 m/s hits a spring (with k=200 N/m), compresses it, and bounces back. What is the maximum compression of the spring?

Solution

In this problem, we are dealing with the potential energy of a spring. So

\  

Note that the final state refers to the spring at maximum compression. From the information given, we know:

REMEMBER:

Velocity is 0 m/s when the spring is at maximum compression (V = 0 during any turnaround).

Conservation of Energy:

  • The law of conservation of energy states that energy cannot be created or destroyed, only transformed from one form to another.
  • Energy is a scalar quantity and can exist in many different forms, including kinetic, potential, thermal, electromagnetic, and chemical energy.
  • The total energy of a system is the sum of all its forms of energy, and this total energy is conserved over time.
  • Energy can be transferred between objects or systems through work or heat transfer.
  • In an isolated system, where there is no external work or heat transfer, the total energy remains constant, and the system is said to be in a state of internal energy equilibrium.
  • The law of conservation of energy is a fundamental principle in physics and is applicable to all physical systems, from the microscopic to the macroscopic scale.

   \n

\