Thermodynamic Basics

• Thermodynamic processes describe how a system exchanges heat (Q), performs work (W), and experiences changes in internal energy (ΔU).

• The First Law of Thermodynamics governs all processes:

  

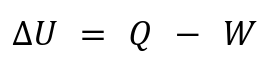
  • ΔU: Change in internal energy.

  • Q: Heat added to the system (positive if absorbed, negative if released).

  • W: Work done by the system (positive if the system expands, negative if compressed).

• Thermodynamic processes play a critical role in systems like heat engines, refrigerators, and turbines, determining energy efficiency and system performance.

Thermodynamic Processes

1. Isothermal Process

• Definition: The system's temperature (T) remains constant throughout the process.

• Key Characteristics:

  • No change in internal energy:
    ΔU = 0 (internal energy depends only on temperature for ideal gases).

  • Heat added to the system is entirely converted into work:
    Q = W

  • Represented on PV diagrams as a hyperbolic curve.

• Work Done:

  • For an ideal gas, work is calculated as:

    

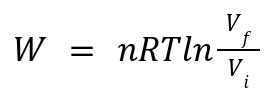
  • where V_f​ and V_i are final and initial volumes, respectively.

• Applications:

  • Expansion or compression of gases in a slow process to maintain thermal equilibrium.

2. Adiabatic Process

• Definition: No heat exchange occurs between the system and surroundings:
  Q = 0

• Key Characteristics:

  • Changes in internal energy are due to work done on/by the system:

    

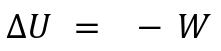
  • Temperature changes as work is done on/by the system.

  • Governed by the equation:

    

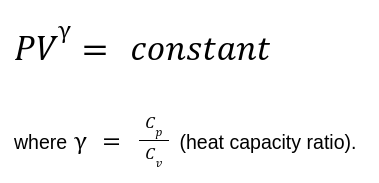
• Work Done:

  • For an ideal gas:

    

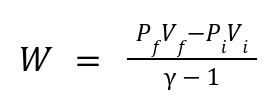
• PV Diagram:

  • Curve is steeper than the isothermal curve due to the absence of heat exchange.

• Applications:

  • Rapid compression/expansion processes, such as in engines or piston systems.

3. Isobaric Process

• Definition: The process occurs at a constant pressure (P).

• Key Characteristics:

  • Allows the system's volume to change while maintaining pressure.

  • Heat added or removed affects internal energy (ΔU) and enthalpy (ΔH).

  • Represented on a PV diagram as a horizontal line.

• Work Done:

  • Work is calculated as:

    

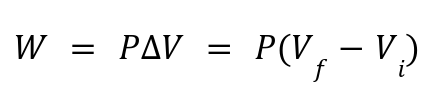
• Applications:

  • Heating or cooling a gas in a container open to the atmosphere.

  • Example: Boiling water at atmospheric pressure.

4. Isochoric Process

• Definition: The process occurs at a constant volume (V).

• Key Characteristics:

  • No work is done since volume does not change:
    W = 0.

  • Any heat added (Q) changes the system's internal energy (ΔU):
    ΔU = Q.

  • Represented on PV diagrams as a vertical line.

• Applications:

  • Heating a gas in a rigid, sealed container (e.g., a pressure cooker)

5. Cyclic Process

• Definition: The system undergoes a series of processes and eventually returns to its initial state.

• Key Characteristics:

  • Net change in internal energy (ΔU) is zero over the entire cycle.

  • The net work done (W) by the system is equal to the net heat added (Q).

  • Often visualized as a closed loop on a PV diagram.

• Applications:

  • Heat engines (e.g., steam engines, internal combustion engines).

  • Refrigeration systems (reversing heat flow).

6. Isentropic Process

• Definition: A reversible adiabatic process where entropy (S) remains constant.

• Key Characteristics:

  • No heat exchange:

    

  • Changes in pressure, temperature, and volume are governed by adiabatic relationships.

• Applications:

  • Idealized processes in turbines, compressors, and nozzles, aiming for maximum efficiency.

7. Throttling Process

• Definition: A process where a fluid's pressure drops as it passes through a restriction or valve without heat exchange.

• Key Characteristics:

  • No work is done on/by the system: W = 0, and Q = 0.

  • Temperature often decreases due to the Joule-Thomson effect.

  • Enthalpy remains constant:

    

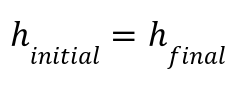
• Applications:

  • Refrigeration cycles and gas expansion systems.

8. Polytropic Process

• Definition: A generalized thermodynamic process that follows:

  

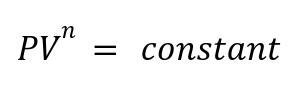
• where n is the polytropic index.

• Key Characteristics:

  • Can represent various processes depending on the value of n:

• n = 0 : Isobaric process.

• n = 1 : Isothermal process.

• n = γ : Adiabatic process.

• Models real gas behavior in engineering scenarios.

• Applications:

  • Compression or expansion of gases in real-life systems.

Applications in Systems

1. Heat Engines and the Carnot Cycle

• Heat engines convert thermal energy into mechanical work.

• Operate between a hot reservoir (T_h) and a cold reservoir (T_c).

• The Carnot cycle is an idealized model with maximum efficiency:

  1. Isothermal expansion: Heat is absorbed from the hot reservoir.

  2. Adiabatic expansion: System does work and cools without heat exchange.

  3. Isothermal compression: Heat is released to the cold reservoir.

  4. Adiabatic compression: System returns to its original state.

• Maximum Efficiency:

  

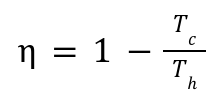
2. Refrigeration Cycles

• Reverse of the Carnot cycle, used to cool systems:

  • Transfers heat from a low-temperature reservoir to a high-temperature reservoir.

• Efficiency is measured using the Coefficient of Performance (COP):

  

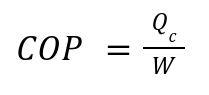
  • Q_c​: Heat removed from the cold reservoir.

  • W: Work input.

• Applications: Refrigerators, air conditioners, heat pumps.