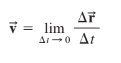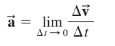Chapter 3: Kinematics in Two Dimensions
3.1: Displacement, Velocity, and Acceleration
- Because displacement in two dimensions cannot be expressed solely in terms of x or y, displacement is often referred as r.
- r is the sum of a 2D displacement vector’s x and y components.
- Following suit, average velocity becomes vₐᵥ = Δr / Δt while instantaneous velocity becomes
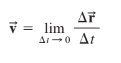
- Values for acceleration remain the same.
- Average acceleration: aₐᵥ = Δv / Δt
- Instantaneous acceleration:
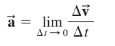
3.2: Equations of Kinematics in Two Dimensions
- Recall how motion can be described in terms of displacement, acceleration, and initial/final velocity.
- In 2D kinematics, all of these variables of motion must be expressed in terms of x and y separately.
- Therefore, the equations remain the same, but include subscripts for x and y.
- However, the time t remains the same for both directions.
| Missing Variable(s) | x Component | y Component |
|---|
| x | vₓ = v₀ₓ + aₓt | vᵧ = v₀ᵧ + aᵧt |
| a | x = 0.5(v₀ₓ + vₓ)t | y = 0.5(v₀ᵧ + vᵧ)t |
| v | x = v₀ₓt + 0.5aₓt² | x = v₀ᵧt + 0.5aᵧt² |
| t | vₓ² + v₀ₓ² + 2aₓx | vᵧ² + v₀ᵧ² + 2aᵧy |
3.3: Projectile Motion
- ==Projectile motion==: motion in a curved (parabolic) two-dimensional path
- In projectile motion, the horizontal and vertical components are studied separately (like in the table)
- Since there is no acceleration in the x direction, the horizontal velocity of a projectile will always remain constant.
- On the other hand, the vertical acceleration will always equal the 9.80 m/s², the acceleration due to gravity
- Projectiles also experience time and speed symmetry.
3.4: Relative Velocity
- Consider the following scenario: A passenger is walking towards another passenger car at the back of a train moving across some tracks.
- What is the velocity of the passenger?
- To answer this question, you would have to consider the velocity of the passenger relative to the train and the velocity of the train relative to the ground.
- The total velocity of the passenger is the velocity of the passenger relative to the train plus the velocity of the train to the ground.
- Generally, if one object is moving in the presence of another moving object, you have to add them together to get the total velocity.
- Other examples:
- An airplane traveling within an air stream.
- A boat crossing a river against/with a current.