Unit 2 - Dynamics ! ⭐️
Forces and Newton’s Laws of Motion
Newton’s Laws of Motion
Newton’s First Law: Mass in motion stays in motion; mass at rest, stays at rest
Think of a car crash, at the instant of impact, car and driver are moving at the same speed
When the car hits the wall, driver continues at the same speed (Object in motion stays in motion)
This is until the person in the car hits the dashboard ☹
Newton’s Second Law
Fnet = ma
An object's mass (m) subjected to forces will undergo an acceleration (a)
Acceleration is directly proportional to the force F and inversely proportional to the mass M
if force doubles = acceleration will double
If mass triples = acceleration will become 1/3
Tells us the magnitude of an object's acceleration in terms of its mass and the force applied
A force applied to an object causes the object to accelerate and the acceleration is in the direction of the net force
Direction of acceleration = same as direction of the force
Acceleration of the object is determined by the net forces acting on it
Newton’s Third law
Every action has an equal and opposite reaction force
Each acts on a different object
Two members of an action/reaction pair have equal magnitudes
Two forces point in opposite directions
What are Forces?
A force is a push or a pull, think of it as a very specific action
You can apply a force on an object or have a force exerted on you by an object
Forces do not exist in isolation from the object that experiences them
Every force has an agent, specific identifiable cause
If a force is being exerted on an object you must be able to identify a specific cause (agent)
A force is not exerted on an object unless you can identify a specific cause/agent
An agent can be an inert object (tabletop or wall)
If an agent exerts a force on an object the object exerts a force on the agent
A force is a vector
When pushing an object you can push it hard or gently, can push in any direction (up, down, left, right)
In order to express the quantities of a push, you need both magnitude and direction
Size and strength of a force is its magnitude
A force can either be a contact force or a long range force
Forces that act on an object by touching it at a point of contact (contact force)
Ex. A baseball on a ball, a hand throwing a ball, you sitting on a chair
Act upon an object without physical contact ( long range force)
Ex. A magnet attracting an object, an object falling due to gravity
A force is an interaction between two objects
Combining forces
When several forces are exerted on an object they combine to form a net force (the vector sum of all the forces)
Net force can be called resultant force
Fnet isn’t a new force acting in addition to the original forces, think of it as all the original forces put together being replaced by Fnet
What do forces do?
How does an object move when a force is exerted on it?
Let's look at a couple examples !
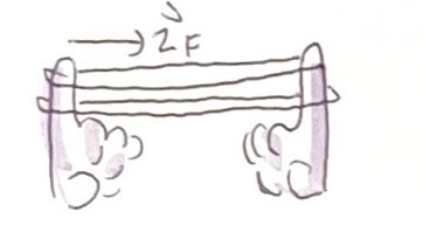
When you stretch a rubber band, it exerts a force because you can feel the pull on your fingers
The rubber band exerts the same force every time you stretch it to the standard length
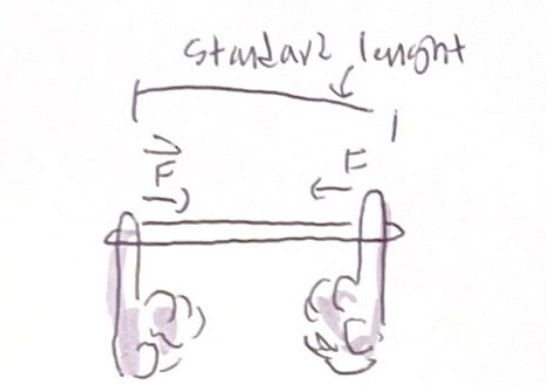
We’ll call the magnitude of this force exerted on your finger the standard force F
When you stretch two identical rubber band to the same standard length the force exerted onto your fingers is now double (2F)
Now place that rubber band on a 1kg block on a frictionless surface
when you stretch the rubber band on the block, the band gets stretched to the standard length
The block experiences the same force F as your finger did, as the block starts to move in order to keep the pulling force constant you must move your hand in the right way to keep the length of the rubber band, thus keeping a constant force
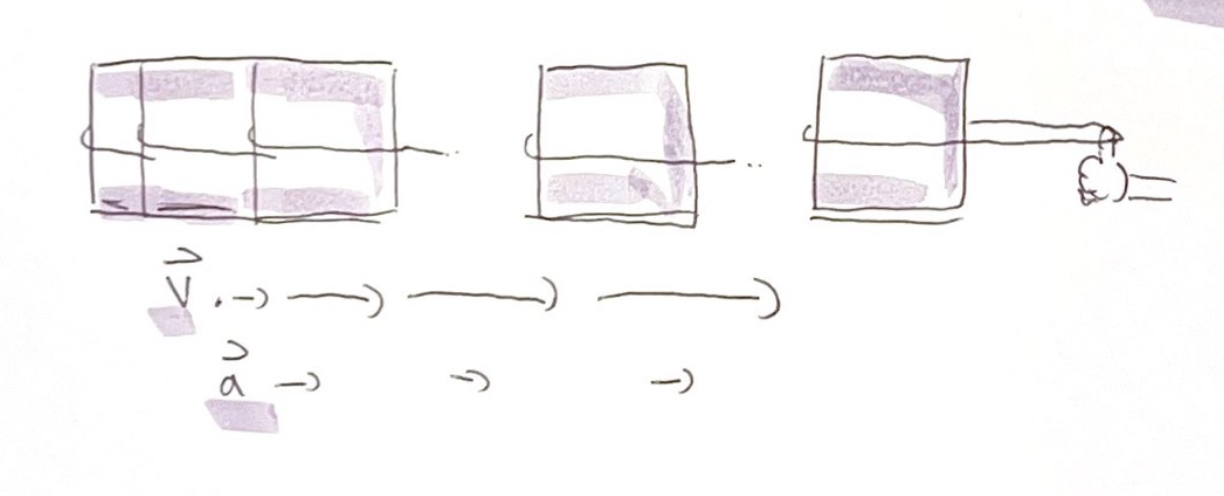
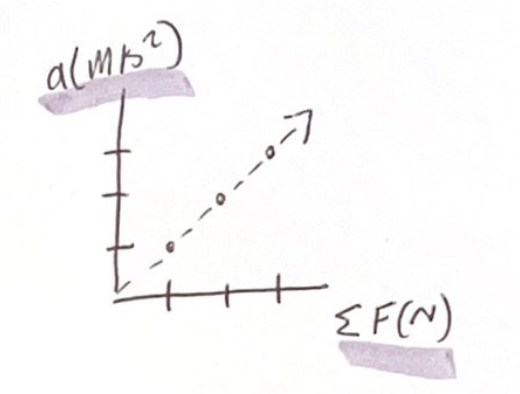
This tells us that as velocity is increasing, the block is staying at a constant acceleration
Since we are also pulling the block with a constant force this tells us very important factors:
An object pulled with a constant force moves with a constant acceleration
Acceleration is directly proportional to force
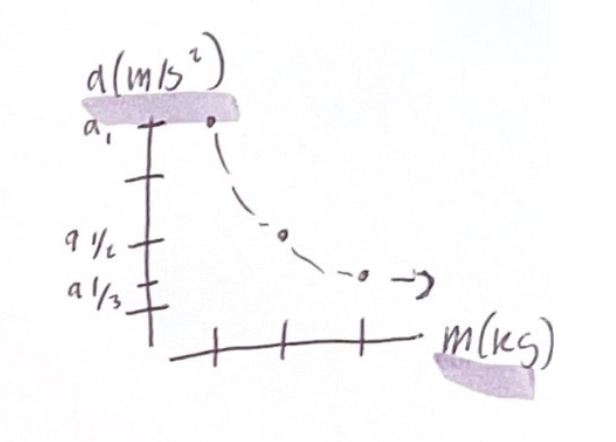
How does acceleration of an object depend on the mass of the object?
Taking the 1kg block and turning it into a 2kg block, twice as much matter
When applying the same force as before with a single rubber band as you did with the 1kg block
You notice that acceleration is one half as great as that of the single block
Glue 3 1 kg blocks together, making a 3 kg object, acceleration is only one-third of the 1kg block’s acceleration
The acceleration is proportional to the inverse of the mass of the object
Acceleration is inversely proportional to an object's mass
Objects with more mass have more inertia
Inertia is the tendency to resist a change in velocity (resist speeding up or slowing down)
Interacting objects
Think of a nail being hit with a glass hammer, the force of the nail on the hammer causes the glass to shatter
If you would push forward a cabinet without it pushing back, you would fall forward
Interaction is the mutual influence of two objects on each other
Action/reaction pair
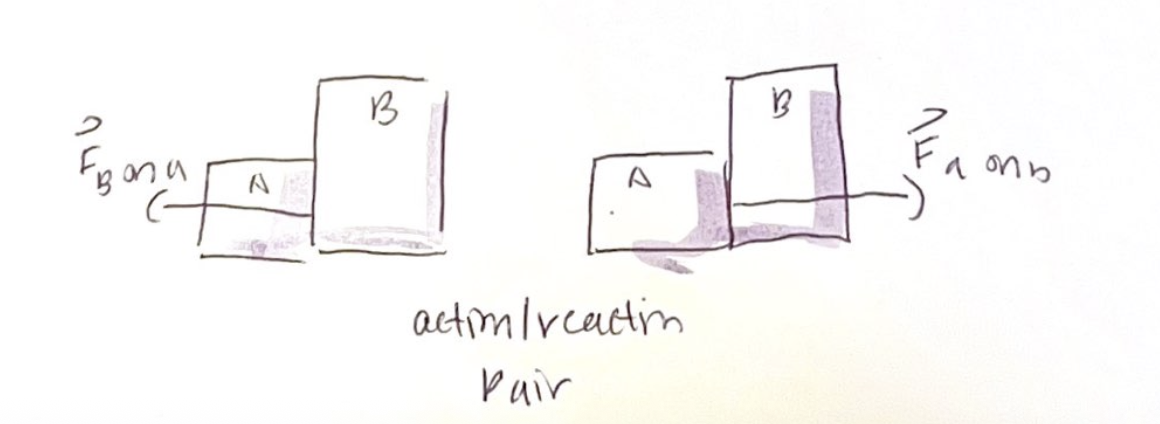
Forces occur simultaneously, cannot say action leads to the reaction
Not a cause and effect, action does not cause the reaction
An action/reaction pair of forces exist as a pair or not at all
Newton’s 3rd law equates to the sizes of the forces NOT their acceleration
When a car and truck get into an accident, they feel forces of equal strength from the other but the car undergoes a greater acceleration than the truck
Be sure to separate the effects (the acceleration) from the causes (the forces themselves)
Two interacting objects can have very different masses, their acceleration can be very different but their interaction forces are the same strength
Applying Newton’s Laws
Mass
Mass is a quantity that describes an object's inertia, the tendency to resist being accelerated
Also describes the amount of matter an object has
Measured in kg
Has the same value wherever the object may be and whatever forces act on it
Mass and weight are NOT the same thing, but they are related
Weight
Weight is the downward pull of gravity
is a force, the gravitational force exerted on an object by a planet
Is a vector, not a scalar, direction is always going straight down
The magnitude of the weight force is directly proportional to the mass, with gravity as the constant of proportionality (W = mg )
The weight of an object is independent of its state in motion
W = mg holds for an object at rest on a table, sliding horizontally or moving in any way
Object's weight is dependant on gravity, value of g varies from planet to planet
Different from mass as mass would be the same no matter the planet, amount of matter does not change, only gravitational force exerted on that matter does
On earth given mass always corresponds to the same weight
Interacting objects cont'd
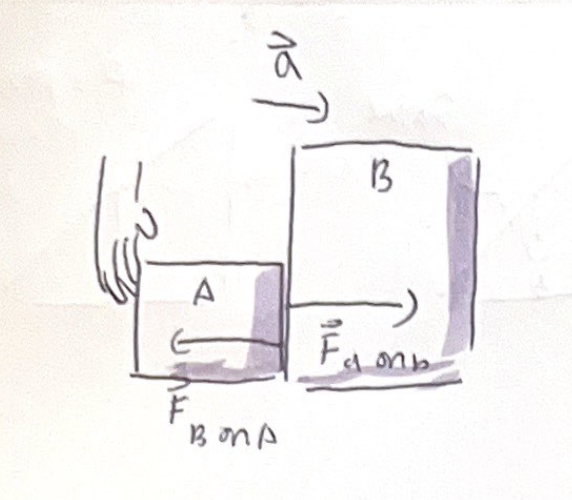
Remember, the forces on A and B are NOT independent
Forces Fb-on-a acting on block a and Fa-on-b acting on block b are an action reaction pair, thus have the same magnitude
Because the two blocks are in contact, their acceleration must be the same
Cant solve for the motion of one block without considering the motion of the other block
Solving motion problems means solving two problems in parallel
Force vectors are always drawn on the free body diagram of the object that experiences the force, NOT the object exerting the force
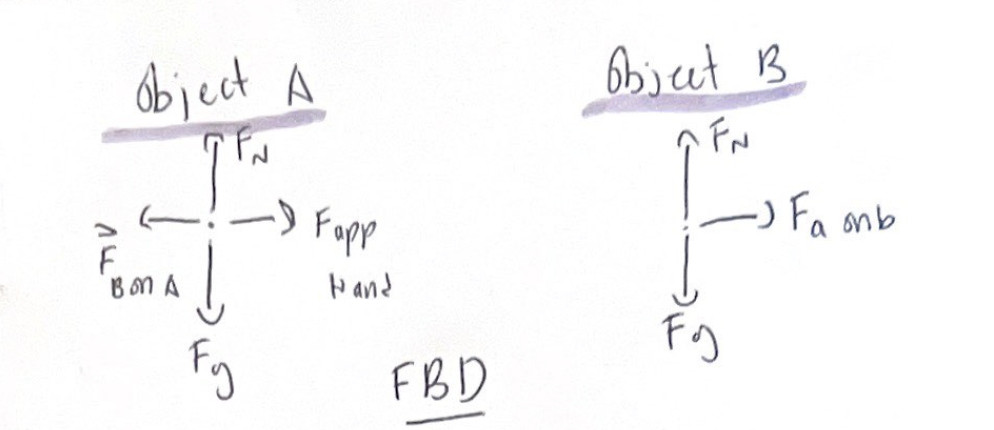
Equilibrium
If an object is at rest, it is in static equilibrium
meaning that acceleration is zero
If an object is moving at a constant speed in a straight line it's in dynamic equilibrium
meaning that acceleration is also zero
In both cases the net force is equal to zero (Fnet = 0)
Apparent Weight
The weight of an object is the force of gravity on that object
Gravity is not a force you can feel or sense directly
The sensation of weight (how heavy you feel) is due to contact forces supporting you

Sensation of weight is due to the normal force exerted on you by the chair, activates the nerves in your skin, what you sense the magnitude of that force
Standing you feel the contact force of the floor pushing against your feet
Hanging from a rope, you feel the friction force between the ropes and your hands
When you are in equilibrium, your weight and apparent weight are generally the same but when you are undergoing acceleration that is not generally the case
You feel “heavy” when an elevator suddenly accelerates upwards while you feel “lighter” as the elevator breaks to a halt
Your true weight w=mg does not change but your sensation of weight has
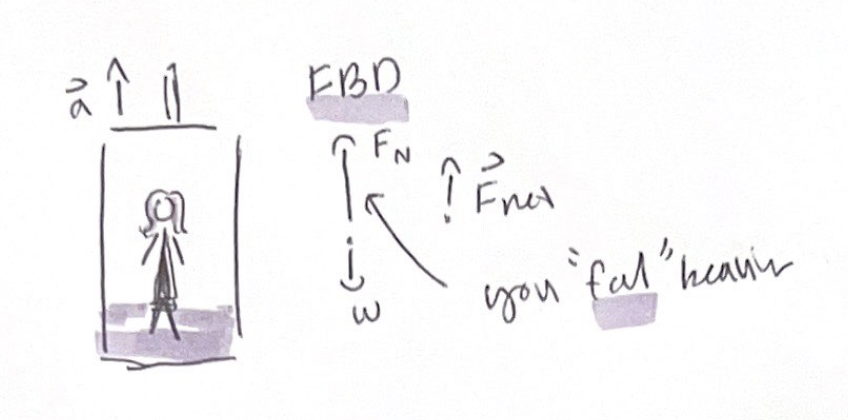
Only force acting on the girl is the upward normal force of the floor and downward weight force
Because there is acceleration, newton's second law states their must be a net force acting in the direction of acceleration
When you are standing on a bathroom scale, the scale is reading the upward force of the scale on you
If you are not accelerating, the upward force is equal to your weight
If the elevator was accelerating up, scale would show an increased weight
Weightlessness
Apparent weight is the contact force supporting an object
A person in free fall has zero apparent weight
Suppose the elevator from before falls and the girl releases a ball from her hand, in the absence of air resistance, bot the man and ball would fall at the same rate
From the girls perspective, the ball would appear to be floating, if she had a scale with
her, then the scale would float beneath her and not press against her feet
Weightlessness does not mean “no weight” an object that is weightless has no apparent weight
The girl’s weight remains the same (mg) because gravity is still pulling her down but she has no sensation of weight
Normal Forces
Always directed perpendicular to the surface
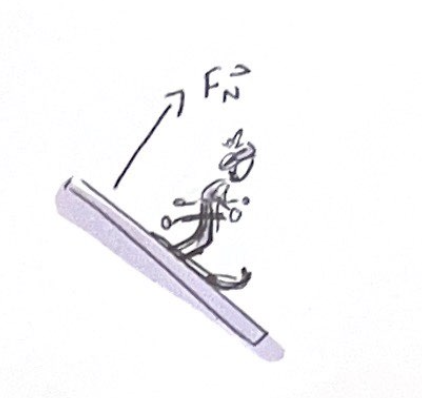
Normal forces originate in the atomic “springs” that make up the surface
The harder it is to push down an object on a surface, the more those “springs” are compressed, the harder they push back up on the object
Normal force adjusts itself so that the object stays on the surface without penetrating it
Responsible for the “solidness” of solids, what prevents you from falling through your chair
When leaning your hand on a wall, you compress the molecular springs in the wall, as a consequence, they push outward against your hand
Surface pushes outwards against the bottom of the skis
Force is perpendicular to the surface
Ropes and Pulleys
Tension force is always in the direction of the string, rope or pulley
A tension force can only pull in the direction of the string
If you try to push with a string, it will go slack and be unable to exert a force
If you pull hard on a rope/string, tension force will become greater
The tension in a massless string or rope equals the magnitude of the force pulling the end of the string or rope
Massless string/rope “transmits” a force from one end to the other
Pull from one end of the rope with force Ft, other end pulls on the object its attached with a force of the same magnitude
The tension in a massless string/rope is the same from one end to the other
Pulley’s
As the string moves, static friction between the string and pulley cause the pulley to turn
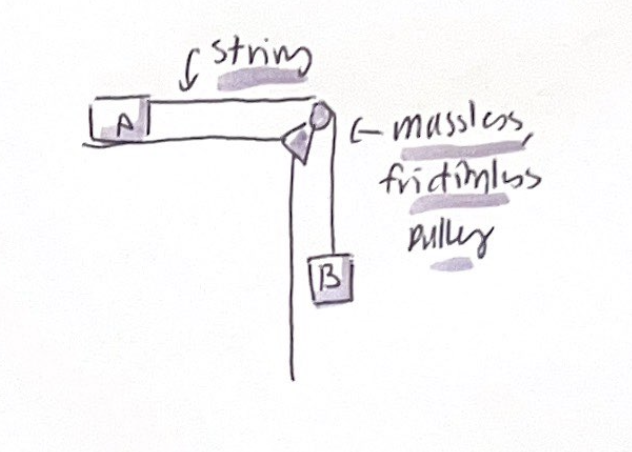
We can assume the following:
The string and pulley are both massless
There is no friction where the pulley turns on its axle
Ideal pulley changes the direction in which the tension force acts but does not change its magnitude
The tension in the string is the same on both sides of the pulley
The tension in a massless string is unchanged by passing over a massless, frictionless pulley
Working with ropes/pulleys
For massless ropes or strings and massless frictionless pulleys:
Tension remains constant throughout the system
Two objects are connected by rope, tension is the same at both ends
When rope passes through pulley, tension in rope is unaffected
Friction
Essential for many things we do, without it we can’t walk, drive, or even sit down
Friction like normal force is exerted by a surface
Friction force is always parallel to the surface
Friction arises when atoms from an object and atoms on the surface collide
Rougher the surface, more the atoms are forced into close proximity, as a result it creates a larger friction force
There are two kinds of friction, Kinetic friction and static friction
Static friction is greater than kinetic friction which explains why it is easier to keep a box moving then it is to start it moving
Static Friction
Is the force that keeps an object “stuck” on a surface, prevents motion relative to surface
Static friction points opposite the direction in which the object would move if there was no friction
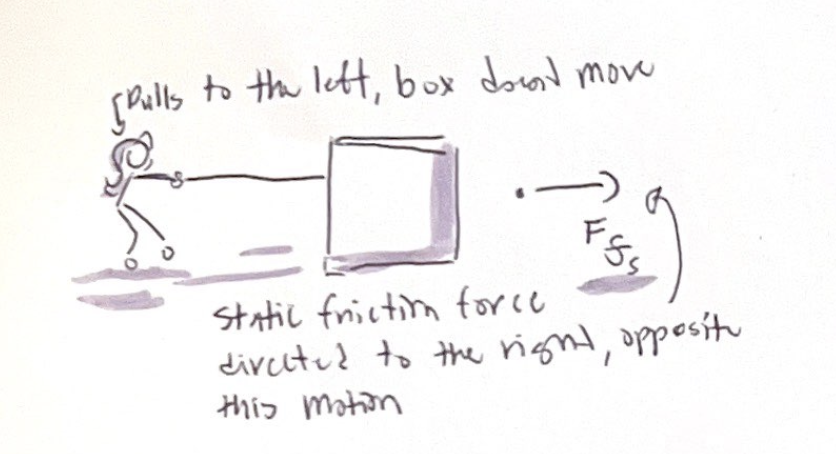
Points in the direction necessary to prevent motion
The force a surface exerts on an object to keep it from sliding/slipping across a surface
Static friction keeps an object from slipping
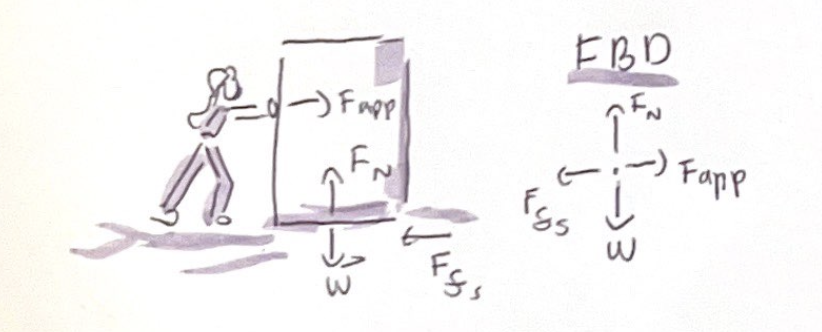
Because the box isn’t moving with respect to the floor, the woman’s push to the right must be balanced by static friction pointing towards the left
Static friction acts in response to an applied force
Static friction force must exactly balance the pushing force
Ffs = Fapp, the harder the woman pushes onto the box, the harder the friction force from the floor pushes back
If she reduces her pushing force, the friction force will automatically reduce to match
There is a limit to how big static friction cna get, if pushed hard enough the box the woman is pushing will slip and start to move across the floor
Static friction force has a maximum possible magnitude of Ffs max
Experiments with friction shows that Ffs max is proportional to the magnitude of the normal force between the surface and the object
So Fs max = (μ)(Fn)
μ (Mu), is called the coefficient of static friction
The coefficient is a number that depends on the materials from which the object and surface are made of
Higher the coefficient of static friction, the greater the “stickiness” between the object and the surface, the harder it is to make an object slide
Keep in mind that static friction does not equal μFn, the value of static friction depends on the force/forces that static friction has to balance in order to keep the object from sliding
Static friction can have any value from zero up to, but not exceeding μFn
Rules for static friction
The direction of static friction, opposes motion
The magnitude of static friction adjusts itself so that the next force is zero and the object doesn’t move
The magnitude of static friction cannot exceed its maximum value Fsmax
Kinetic Friction
Acts as an object slides across a surface
A force that always “opposes the motion” means that the friction force on a sliding object points in the opposite direction of the object's motion
Once the block starts sliding, friction force is replaced by kinetic friction (sliding friction)
The direction of kinetic friction unlike static, has a nearly constant magnitude given by:
Ffk = μkFn
μk is called to coefficient of kinetic friction
Kinetic friction like static friction is proportional to the magnitude of the normal force
The magnitude of kinetic friction does NOT depends on how fast the object is sliding
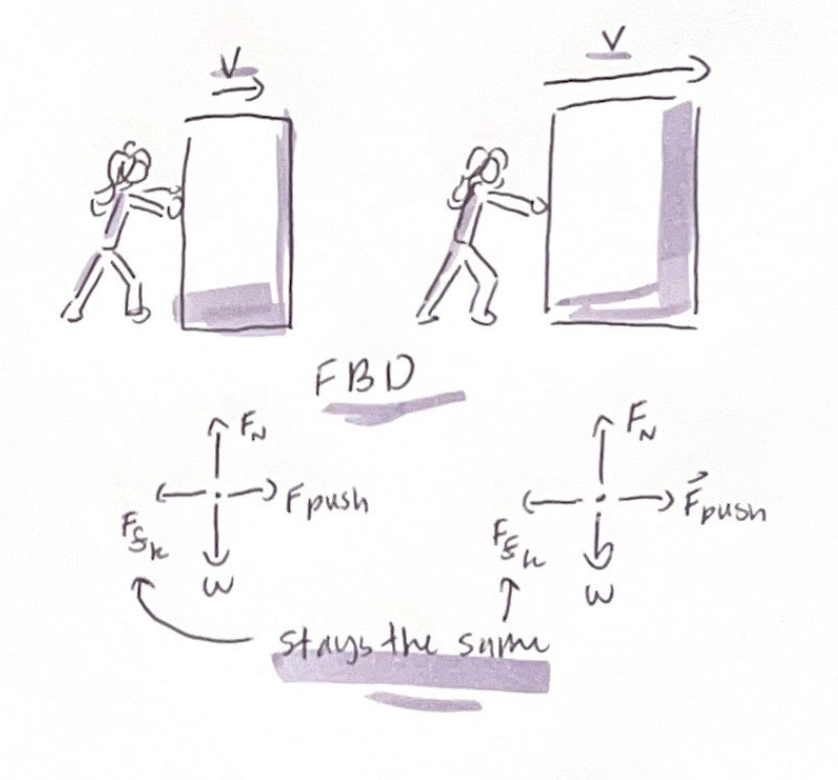
The kinetic friction force is the same no matter how fast the object slides
Motion on a ramp
Accelerated motion on a ramp
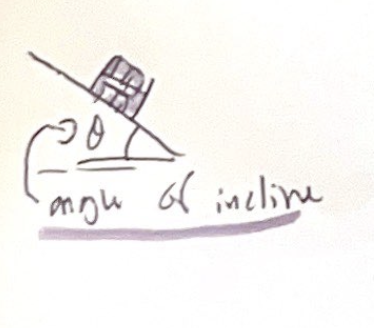
The crate accelerates due to gravity, which pulls it down the incline, resulting in an increase in its velocity as it moves further down the ramp.
We know there is acceleration because velocity is changing, both being parallel to the ramp
Unless the object is stationary or moving at a constant velocity, there will be a component of acceleration along the incline due to gravity.
The steeper the incline, the larger the component of gravity pulling the object down the slope, and thus the greater the acceleration.
The forces on an object on an incline
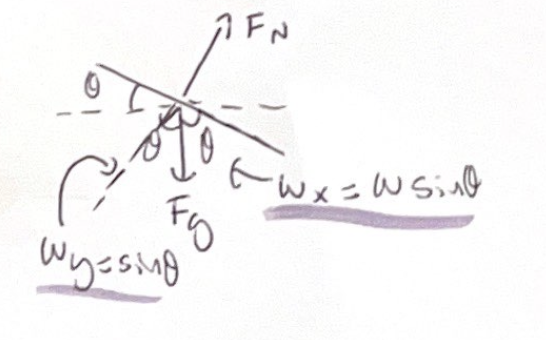
Fn always points perpendicular to the surface
Weight force always points straight down
When rotating x-axis to align with inline, angle between Fg and y-axis is the same as the angle of the slope
Weight can be decomposed into y and x components
Weight-y is negative because weight points in the negative y-direction
Mass does not affect acceleration as you are going down an inclined plane
Gravity is pulling the object down, gravity is proportional to mass
Force of gravity is the force of acceleration
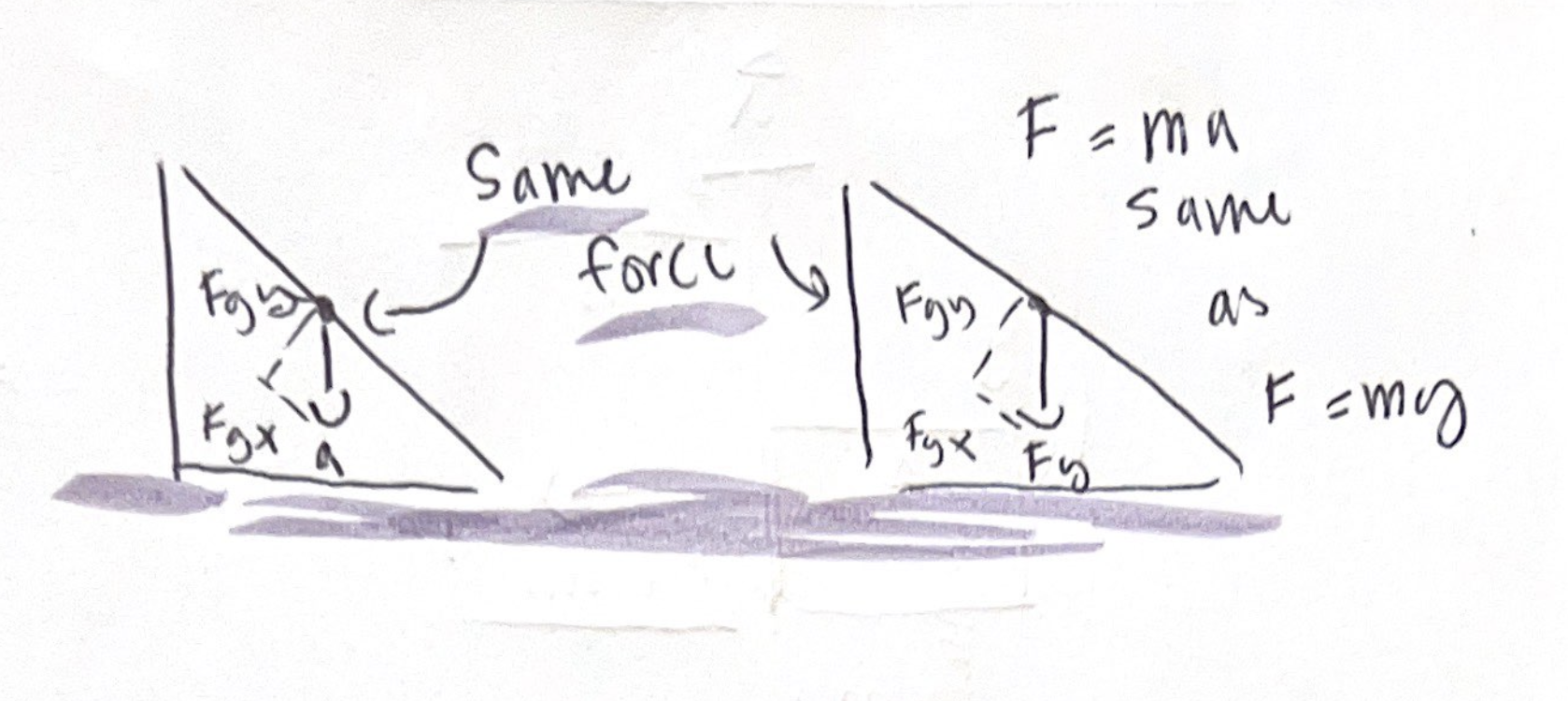
Doubling mass makes gravity pull twice as hard, but also requires twice as much force to get the same acceleration