12-06: Logarithms (I)
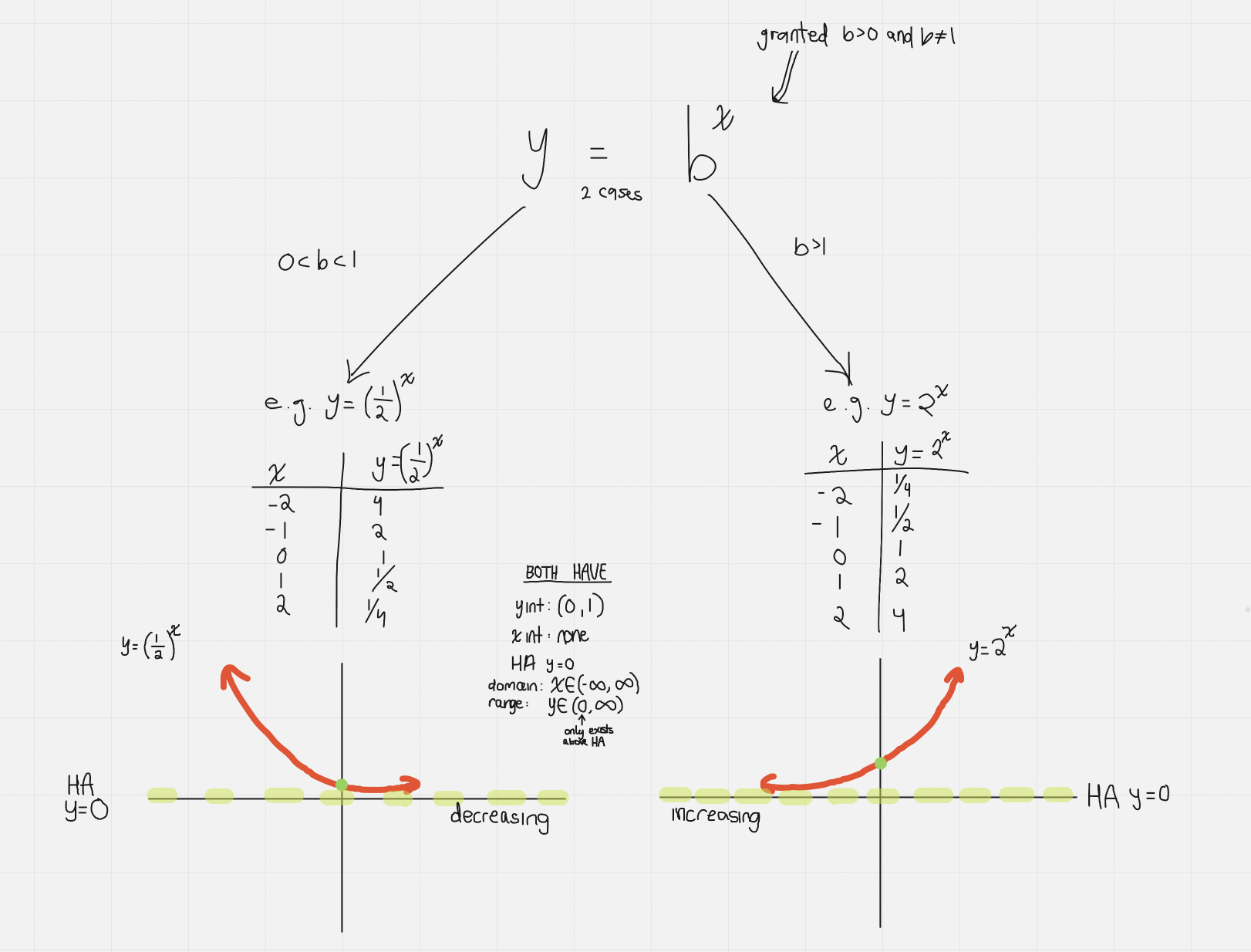
Exponential function
f(x) = bˣ
Variable in the exponent
Base is a positive number that is not 1
Polynomial functions have a constant difference (obtained from subtraction)
Exponential functions have a constant ratio (obtained from division)
Inverse
f⁻¹(x)
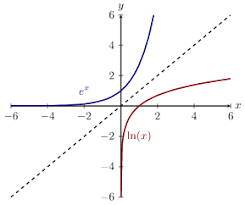
From graphs (reflection over line y=x, swap x and y values):
f(x) → f⁻¹(x)
(x,y) → (y,x)
(-2,3) → (3,-2)
Swap domain and range
From equations:
Change f(x) into y
Switch x and y
Solve for y
Replace y with f⁻¹(x), if it is a function
Summary: exponential functions (y=bˣ) vs. inverse functions (y=bʸ)
Exponential functions (y=bˣ) | Inverse functions (y=bʸ) | |
|---|---|---|
Domain | D: xE(-∞, ∞) | D: xE(0, ∞) |
Range | R: yE(0, ∞) | R: yE(-∞,∞) |
x-int | none | (1,0) |
y-int | (0,1) | none |
Asymptote | HA y=0 | VA x=0 |
y=bˣ where b>1
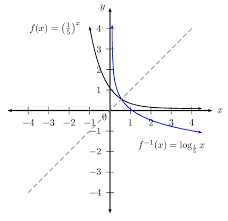
y=bˣ where 0<b<1 (flips through the diagonal)
Logarithms
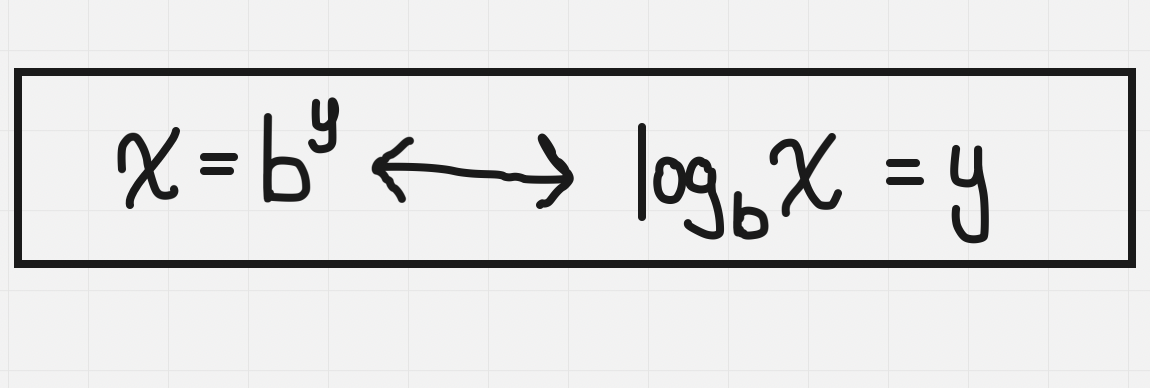
Logarithm: the logarithm (log) of a number is the value of the exponent to which a given base must be raised
e.g. log₂8 → log (base 2) of 8 → essentially means: what power of 2 gives us 8?
2³ = 8∴ log₂8 = 3
Any exponential relationship can be written using log notation
Common log
If there is no base on a log (b) then there is an assumed 10 as a base
log₁₀x = logx
Same base for log and for an exponent:
Logs cross out and we’re left with just the exponent which becomes our answer
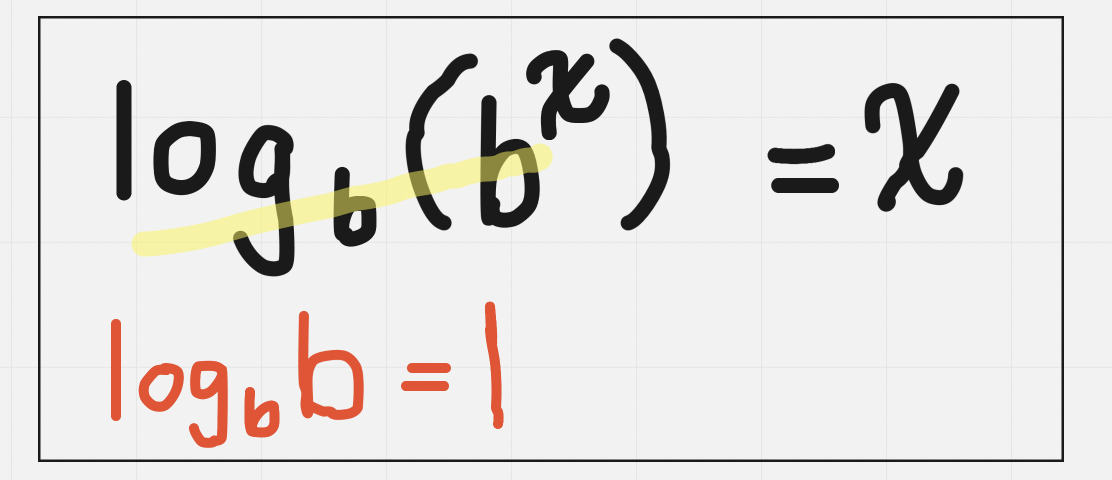
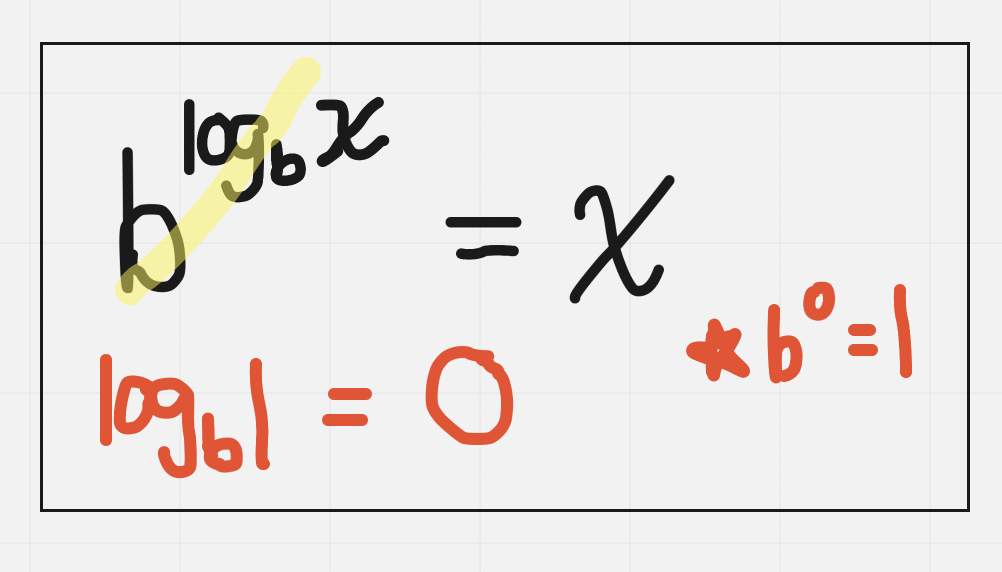
Log Functions
Log function: inverse of an exponential function
This is the baseline of what will be used and operated on, as well as transformed
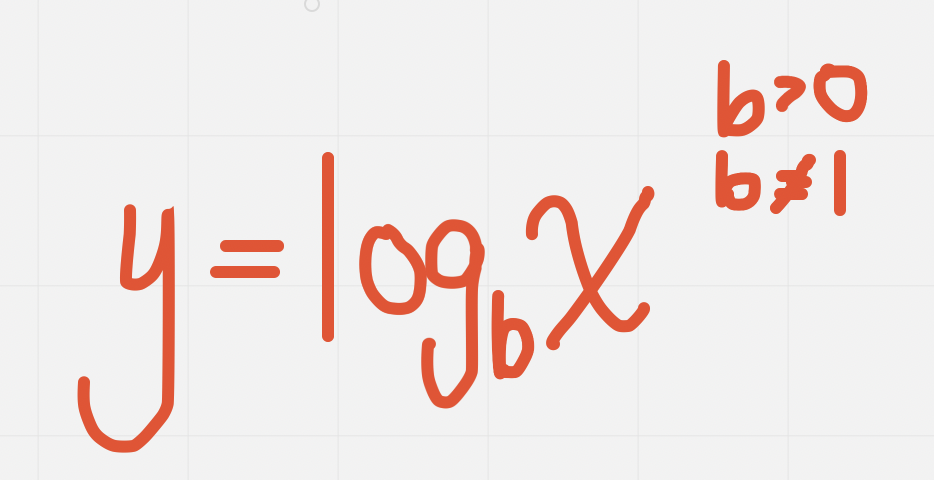
Transformations
Same as usual, with log and its base being the exception, as these allow for us to find our base value

Power Law of Logs
Allows for us to move an exponent to the front of a log so that it can be operated on differently. Allows for us to find the value of harder to operate on values
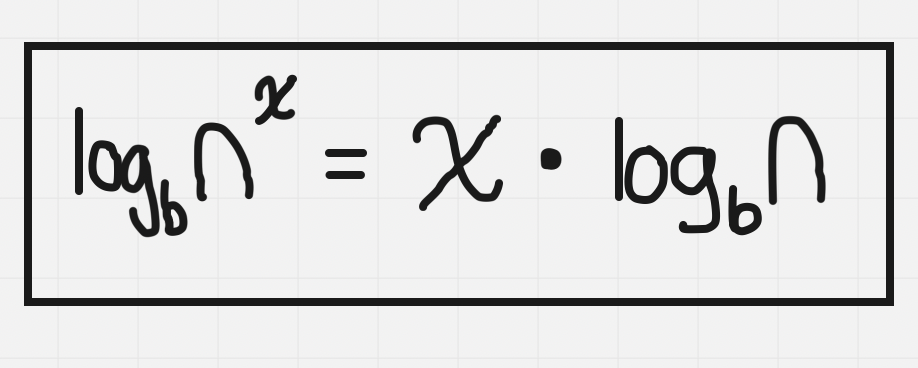
Change of Base
Allows for us to simplify and change the look of logs
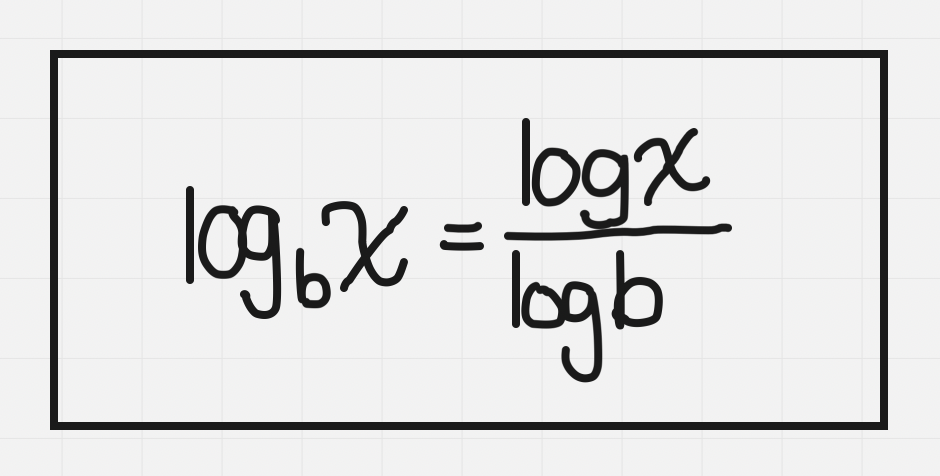
Log in Physical Science
Formulas and meaning behind 3 major concepts

Log Rules Summary

