Chapter 7: Rotational Motion
Parallel Forces
- Parallel forces act in the same direction on an object but have different application points.
- When two or more parallel forces act on an object, they produce a resultant force that is equal to the vector sum of the individual forces.
- The resultant force of parallel forces can be calculated using the principle of moments, which states that the sum of the clockwise moments must be equal to the sum of the anticlockwise moments.
- The moment of a force is the product of its magnitude and the perpendicular distance from its line of action to the point about which moments are being calculated.
- Parallel forces can be either concurrent or non-concurrent. Concurrent parallel forces have their lines of action passing through a common point, while non-concurrent parallel forces do not.
- The weight of an object is an example of a parallel force, as it acts vertically downwards and has its point of application at the center of mass of the object.
- The tension in a rope or cable that is pulling an object is also an example of a parallel force, as it acts along the direction of the rope or cable and has its point of application at the point where the rope or cable is attached to the object.
- Parallel forces can produce either translational motion or rotational motion in an object, depending on the point of application of the forces.
- When two or more parallel forces act on an object and their lines of action do not coincide, a torque is produced that tends to rotate the object about an axis perpendicular to the plane of the forces.
- Parallel forces can be resolved into their components using trigonometry, which allows the calculation of the individual forces acting in different directions.
- The concept of parallel forces is important in many areas of physics, including mechanics, engineering, and astronomy, as it allows the analysis of the effects of multiple forces acting on an object or system.
Sample Problem
A 45-kg girl and a 65-kg boy are sitting on a seesaw in equilibrium. If the boy is sitting 0.7 m from the fulcrum, where is the girl sitting?
Solution
In equilibrium:
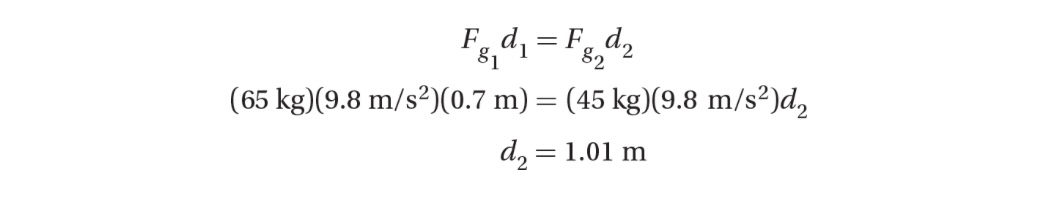
Torque
Torque is a measure of the twisting force that is applied to an object when a force is applied to it at a distance from the object's axis of rotation.
TIP:
Torque produces rotation.
The magnitude of torque is given by the product of the force applied and the distance from the axis of rotation at which the force is applied.
The direction of the torque is given by the right-hand rule, where the fingers of the right-hand curl in the direction of rotation, and the thumb points in the direction of torque.
Torque is a vector quantity, which means that it has both magnitude and direction.
The SI unit of torque is the newton-meter (N⋅m), which is equivalent to the joule (J).
Torque is important in many aspects of physics, including rotational motion, angular acceleration, and angular momentum.
Torque is used to describe the motion of objects that rotate around a fixed axis, such as a wheel or a gear.
Torque is also important in engineering, where it is used to design and analyze structures that are subjected to twisting forces, such as bridges and buildings.
In order to produce the maximum torque on an object, the force must be applied at a distance from the axis of rotation that is perpendicular to the line connecting the axis of rotation and the point of application of the force.
Torque is often used in conjunction with other physical concepts, such as work, energy, and power, to analyze and understand the behavior of rotating objects.
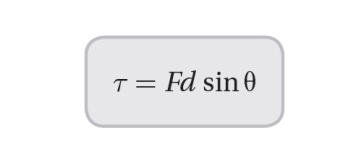
Inertia
Inertia is the tendency of an object to resist a change in its state of motion.
It is a property of matter that causes an object to maintain its current velocity and direction of motion unless acted upon by an external force.
The amount of inertia an object has is directly proportional to its mass, the greater the mass, the greater the inertia.
Inertia is described by Newton's first law of motion, also known as the law of inertia, which states that an object at rest will remain at rest, and an object in motion will continue in motion with a constant velocity, unless acted upon by a net external force.
Inertia can be observed in everyday life, such as when a car comes to a sudden stop and passengers feel a force pushing them forward, due to their bodies' inertia resisting the change in motion.
Inertia can also be seen in planetary motion, as planets continue to move in their orbits around the sun due to their inertia and the gravitational force acting upon them.
Inertia can be measured by observing an object's acceleration in response to a known force, as described by Newton's second law of motion.
Inertia is a key concept in the development of modern physics, particularly in the field of relativity, where it is incorporated into the theory of general relativity.
Inertia can be thought of as a measure of an object's resistance to a change in its state of motion and is related to the object's energy and momentum.
Inertia is an important consideration in many areas of engineering, particularly in the design of vehicles and structures, where it can affect stability, maneuverability, and structural integrity.
TIP:
The AP Physics 1 exam will not ask you to calculate moments of inertia; however, you must understand them and be able to use them.
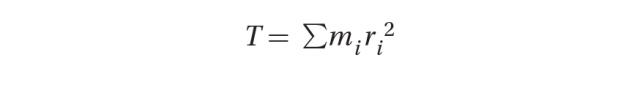
Angular Kinematics
Angular position is the measure of the angle an object has rotated from some reference point.
Angular displacement is the change in angular position and is equal to the final angular position minus the initial angular position.
Angular velocity is the rate of change of angular position and is equal to the change in angular position over the change in time.
Angular acceleration is the rate of change of angular velocity and is equal to the change in angular velocity over the change in time.
The direction of angular velocity and acceleration are determined by the right-hand rule, with the thumb pointing in the direction of the angular velocity or acceleration and the fingers curling in the direction of rotation.
Centripetal acceleration is the acceleration towards the center of a circular path and is equal to the square of the tangential velocity divided by the radius of the circular path.
Centripetal force is the net force that acts towards the center of a circular path and is equal to the mass of the object times the centripetal acceleration.
The relationship between tangential speed, angular speed, and radius of curvature is given by v = ωr, where v is tangential speed, ω is angular speed, and r is the radius of curvature.
Likewise, angular acceleration (caused by torques) is defined kinematically by:
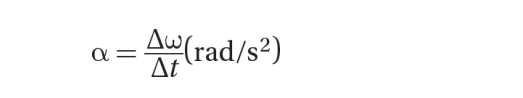
The period of an object in circular motion is the time it takes to complete one full rotation and is equal to 2π divided by the angular velocity.
The frequency of an object in circular motion is the number of rotations per unit of time and is equal to the inverse of the period.
Torque is the measure of a force's ability to cause rotational motion and is equal to the force times the lever arm (the distance between the force and the axis of rotation).

Energy Conservation
- The energy conservation principle states that the total energy of a closed system remains constant, regardless of internal changes in the system.
- Energy can be transferred between different forms, but it cannot be created or destroyed, only transformed from one form to another.
- Mechanical energy is the sum of the kinetic energy and potential energy of an object or system.
- The conservation of mechanical energy applies to systems in which only conservative forces act.
- Nonconservative forces, such as friction or air resistance, cause mechanical energy to be transformed into other forms of energy, such as heat or sound.
- Work-energy principle relates the work done on an object to its change in kinetic energy.
- Power is the rate at which work is done or energy is transferred and is measured in Watts.
- Energy can be stored in a variety of ways, including elastic potential energy, gravitational potential energy, and electrical potential energy.
- Energy can also be stored in chemical bonds or in nuclear particles and released through chemical reactions or nuclear processes.
- Energy efficiency refers to the ratio of useful output energy to input energy and can be improved through technology or behavior changes.
- The concept of angular momentum is closely related to rotational kinetic energy, and the two quantities are often used together to analyze the behavior of rotating objects and systems.
Angular Momentum
Angular momentum is the rotational analog of linear momentum and is defined as the product of an object's moment of inertia and its angular velocity.
Angular momentum is a conserved quantity, meaning that the total angular momentum of a system is constant in the absence of external torques.
The direction of angular momentum is perpendicular to the plane of rotation and is described by the right-hand rule.
The moment of inertia depends on the distribution of mass and the axis of rotation of an object.
Objects with larger moments of inertia require more torque to produce the same angular acceleration as objects with smaller moments of inertia.
The angular velocity of an object undergoing uniform circular motion is constant in magnitude but changing in direction, and therefore has a nonzero angular acceleration.
An external torque can change the angular momentum of an object or system, causing it to rotate faster or slower, or to change direction.
In the absence of external torques, the angular momentum of an isolated system is constant, a principle known as the conservation of angular momentum.
Angular momentum conservation can be applied to a wide range of physical systems, including planetary orbits, spinning tops, and atoms.
The conservation of angular momentum can be used to explain many phenomena, such as the precession of a gyroscope, the behavior of magnetic dipoles, and the formation of accretion disks around black holes.
\n