6.1 - Intro To Trigonometry

Overview of Trigonometry

Trigonometry is a branch of mathematics focused on the relationships between the angles and sides of triangles. It is particularly useful for determining:

• Lengths of missing sides

• Sizes of missing angles

• Areas of triangles

While trigonometry is often associated with right-angled triangles, it is commonly applied to all types of triangles in practical scenarios.

Key Concepts in Trigonometry

When approaching exam questions related to triangles, the primary challenge is often identifying the appropriate equations to use. The following flow diagram can help guide the decision-making process:

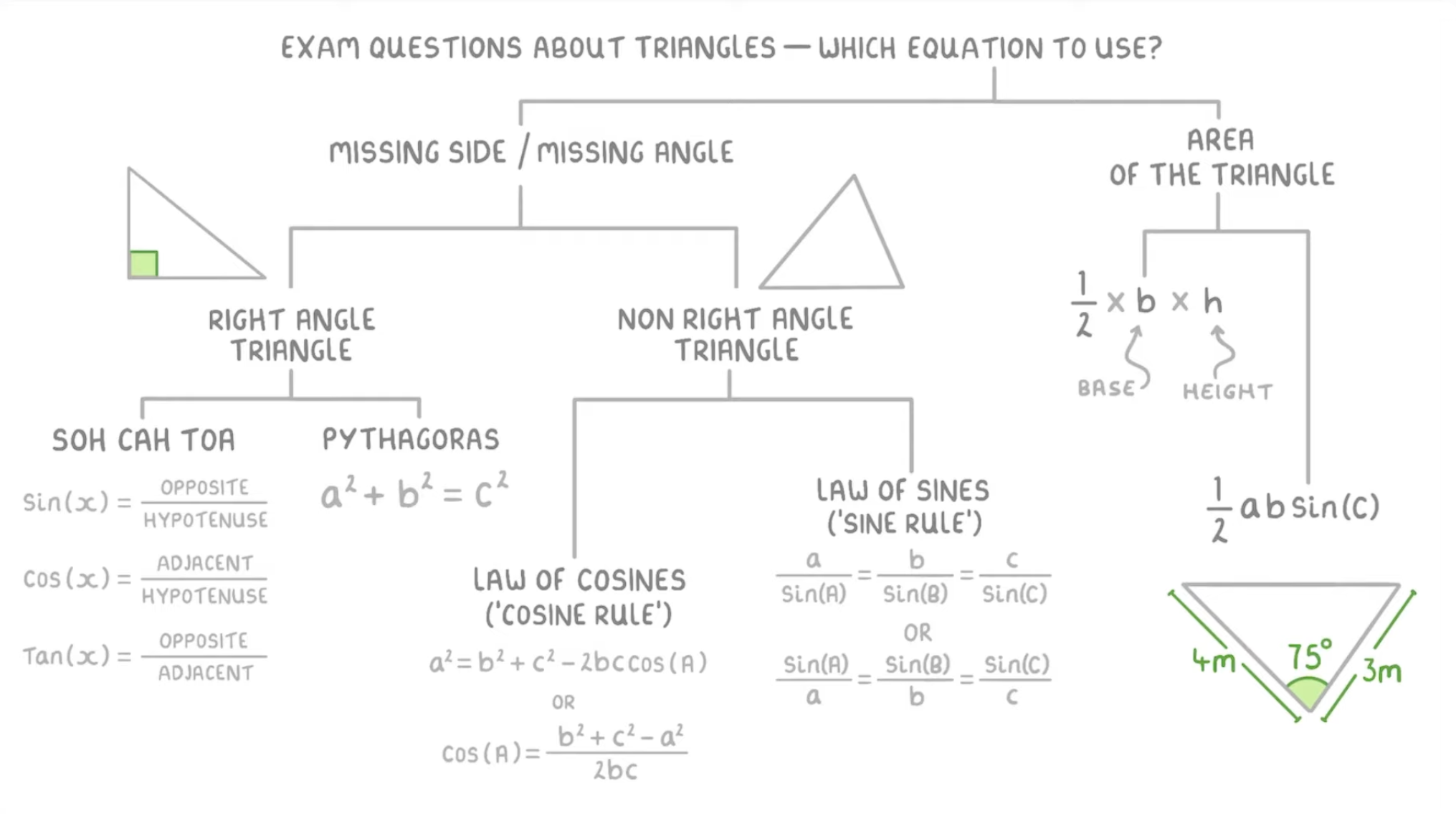
Identifying the Problem Type

1. Determine if you are looking for:

   • A missing side

   • A missing angle

   • The area of the triangle

2. Classify the triangle:

   • Right-angled triangle

   • Non-right-angled triangle (e.g., scalene triangle)

Equations for Right-Angled Triangles

If the triangle is a right-angled triangle, the following equations are typically used:

• Pythagorean theorem

• SOHCAHTOA (sine, cosine, tangent relationships)

Equations for Non-Right-Angled Triangles

For non-right-angled triangles, the following laws are applicable:

• Law of Cosines (Cosine Rule)

• Law of Sines (Sine Rule)

Finding the Area of a Triangle

To calculate the area of a triangle, you can use one of two equations based on the information available:

• If the base and height are known, use the area formula: Area = 1/2 × base × height

• If two sides and the included angle are known, use the formula: Area = 1/2 × a × b × sin(C)

Conclusion

This video serves as a brief overview of the main equations and concepts in trigonometry. Future videos will delve deeper into each equation, explaining their applications and how to use them effectively. If you found this introduction helpful, consider liking and subscribing for more content.