Sound

• In both fluids and solids (collectively known as bodies) there are internal forces acting between the 'elements' of the body. These internal forces are known as stress.

  • Stress is the average force per unit area that an element of a body exerts on an adjacent element across an imaginary surface that separates them.

• In general, the stress across the surface between two elements may be in any direction relative to the normal of the surface.

  • Stress is divided into normal stress and shear stress.

• In a fluid, the normal stress is the pressure.

• Sound is a wave of stress in a body that acts as the medium.

• In fluids sound only has a longitudinal form; in solids, it can be both longitudinal and transverse.

• In a fluid, the elements move (are displaced) in the direction of the sound wave.

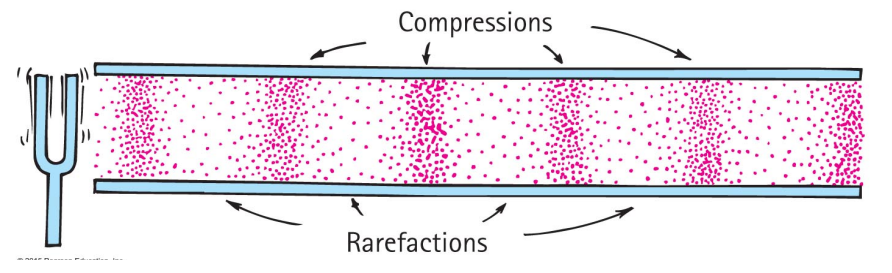
• Where the fluid elements are squeezed together we find high pressure (compressions), where they have spread apart we find low pressure (rarefactions).

Musical Notes

• A musical note is a sound wave with a specific frequency.

• An octave corresponds to a doubling of frequency

• The ratio of frequencies of adjacent notes is constant, ^12√2

• The range of human hearing is ~20 Hz to ~20,000 Hz.

  • Other animals can hear sounds with frequencies well below (elephants, whales) and well above (dogs, bats) this range.

• Sound waves with frequencies below 20 Hz are called subsonic, and sound waves with frequencies above 20,000 Hz are called ultrasonic.

• In general, the speed of sound in a solid is higher than in a liquid which is higher than in a gas.

• At a given P and T, less dense gases have higher sound speeds.

• The speed of sound in gas increases with P and T.

• If an object travels faster than the speed of sound in a medium its speed is described as supersonic.

EXAMPLE 1:

How do the frequency and wavelength of a sound wave change when it passes from air into water?

• Increase in speed

• Frequency stays the same

• Wavelength increases

EXAMPLE 2:

You see a flash of lightning then 2 seconds later hear the thunder. How far away did the lightning strike the ground? Note the speed of light is so high (3 x 10^8 m/s, almost a million times faster than sound) that the time for light to travel to us is negligible compared to the time for the sound.

• d= V_sound x time

• 343 m/s x 2 = 686 m or 1/2 mile

Beats

• Interference can also occur between waves with different frequencies fA and f B. Consider two waves with different frequencies fA and fB.

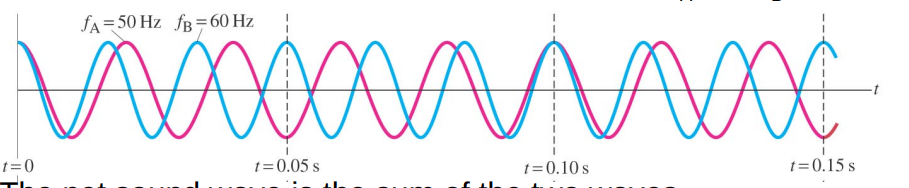
• The net sound wave is the sum of the two waves

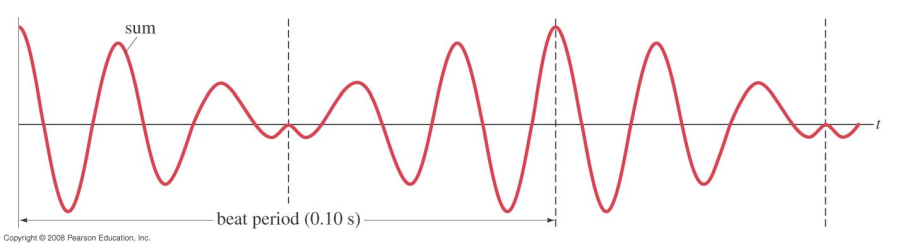
• The frequency difference |fA – fB| is called the beat frequency.

EXAMPLE 1:

A tuning fork produces a steady 400 Hz tone. When this tuning fork is struck and held near a vibrating guitar string, twenty beats are counted in five seconds. What are the possible frequencies produced by the guitar string?

• f_beat = 20/5 = 4 Hz.

  • f_beat = |f_TF - f_G)|

  • f_beat = |f_TF - f_G)| > 4 = |400 - x|

  • 4 - 400 = x > |-396| = x OR 4 + 400 = x > |404| = x

• F_G = 396 OR 404

Musical Instruments

• When a musical instrument is played the instrument vibrates.

• To produce a note the vibrations must be dominated by a single frequency.

• The instrument – or some part of it - is designed to support standing waves.

• The vibrations of the instrument cause the fluid elements of the nearby air to be displaced changing the local pressure.

• The pressure disturbances then travel through the air to a detector such as your ear.

• The frequencies of the sound in the air are the same as the frequencies of the vibration of the instrument.

• The wavelengths of the sound in air are not, in general, the same as the wavelengths of the standing waves on the instrument.

  • The speed of waves on the instrument can be different from the speed of sound in air.

• Usually, several standing waves are produced when the instrument is played – the fundamental usually dominates but the overtones also appear.

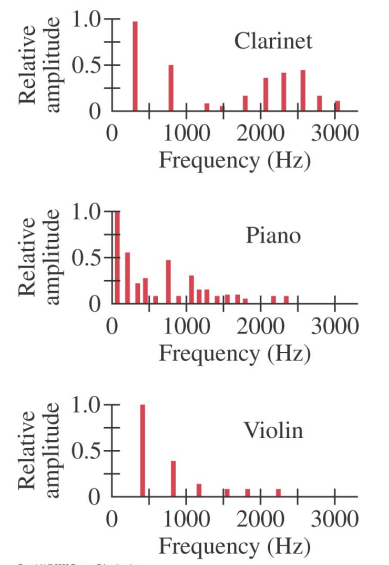
Stringed Instruments

• We have already considered the standing waves on taut strings. The ends of the string are fixed and correspond to nodes.

• The fundamental has a wavelength twice the length of the string. The overtones have wavelengths which are the integer fractions of the fundamental.

  • λ1=2 L

  • λ_n =λ_1/n

• The frequency of the fundamental and the overtones are:

  • f_1= v / λ_1

  • f_n =n (f_1)

• The speed v is the speed of waves on the string and depends upon the tension FT in the string.

• When you tune a stringed instrument you change the tension FT

  • This changes the speed v of waves on the string.

• The change in v changes the frequencies of the harmonics.

• Tuning the instrument does not change the wavelengths of the standing waves.

• When you play a stringed instrument such as a guitar or a violin you change the length of the string.

• This changes the wavelengths of the standing waves which changes the frequency of the waves.

• The speed of the waves upon the string remains the same.

Wind Instruments

• The notes from wind instruments are from standing waves of sound – air pressure/displacement - within a column of air (tube).

• The sound waves in the instrument are generated by blowing into the instrument and (usually) causing some object (reed or lips) to vibrate.

• The column of air is 3D: in order to restrict the number of standing waves produced when the instrument is played the pipe is usually long and narrow.

• There is one big difference between string and wind instruments:

  • the ends of the column of air can be nodes or antinodes depending upon whether they are open or closed.

Open Tubes

• For open tubes (as in a flute) the ends of the tube are nodes of pressure and antinodes of air displacement.

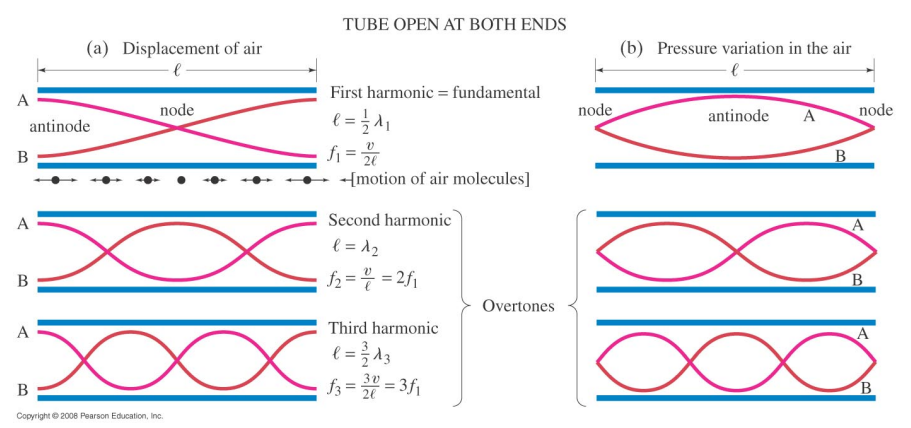
• The relationship between the fundamental and the overtones is the same as for a string.

Closed Tubes

• For closed tubes, the open end of the tube is a node of pressure (antinodes of displacement), and the closed end is an antinode of pressure (node of displacement).

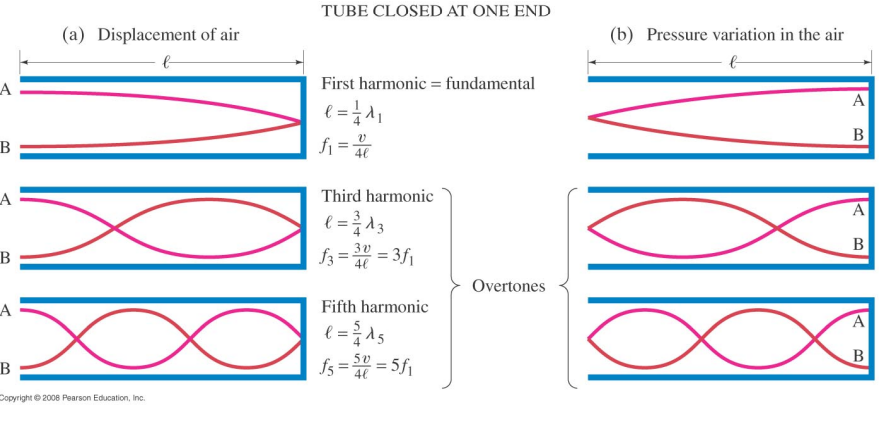
• For a closed tube only the odd harmonics appear.

• Organs of all types have lots of tubes (pipes) with both open and closed ends. For a flute, clarinet, trumpet, etc. the length of the air column is changed by either covering/uncovering holes or with valves.