Chapter 1: Vectors
Vectors:
- A vector is a mathematical quantity that has both magnitude and direction.
- Vectors can be represented graphically using arrows, where the length of the arrow represents the magnitude of the vector and the direction of the arrow represents the direction of the vector.
- Vectors can be added together to form a resultant vector, which represents the combination of the original vectors.
- The magnitude of the resultant vector can be found using the Pythagorean theorem, and the direction of the resultant vector can be found using trigonometry.
- Vectors can be multiplied by scalars to change their magnitude or direction.
- The dot product of two vectors can be used to find the angle between them and the magnitude of their projection onto each other.
- The cross product of two vectors can be used to find a vector that is perpendicular to both original vectors.
- Vectors are used in many areas of physics, including mechanics, electromagnetism, and quantum mechanics.
Coordinate Systems and Frames of Reference:
A coordinate system is a mathematical system used to define the position of objects in space.
A frame of reference is a set of reference points used to describe the motion of an object.
The choice of coordinate system and frame of reference can affect the way that the motion of an object is described.
In physics, the most commonly used coordinate system is the Cartesian coordinate system, which uses three axes (x, y, and z) to define position in three-dimensional space.
The choice of origin (the point at which the axes intersect) can affect the position of objects in the coordinate system.
Frames of reference can be either inertial (non-accelerating) or non-inertial (accelerating).
In non-inertial frames of reference, fictitious forces such as centrifugal and Coriolis forces can arise.
The choice of frame of reference can affect the way that the motion of an object is perceived and can be used to simplify calculations.
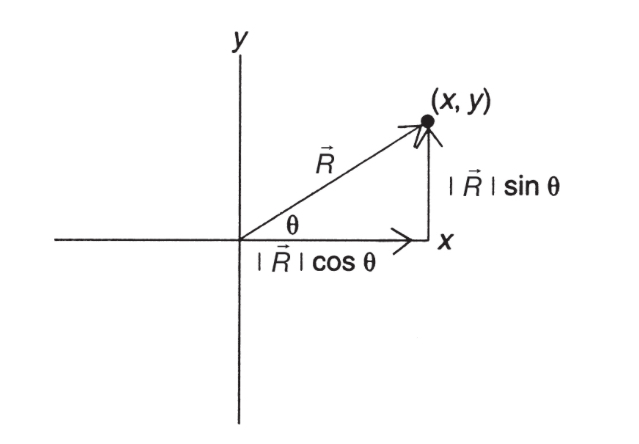
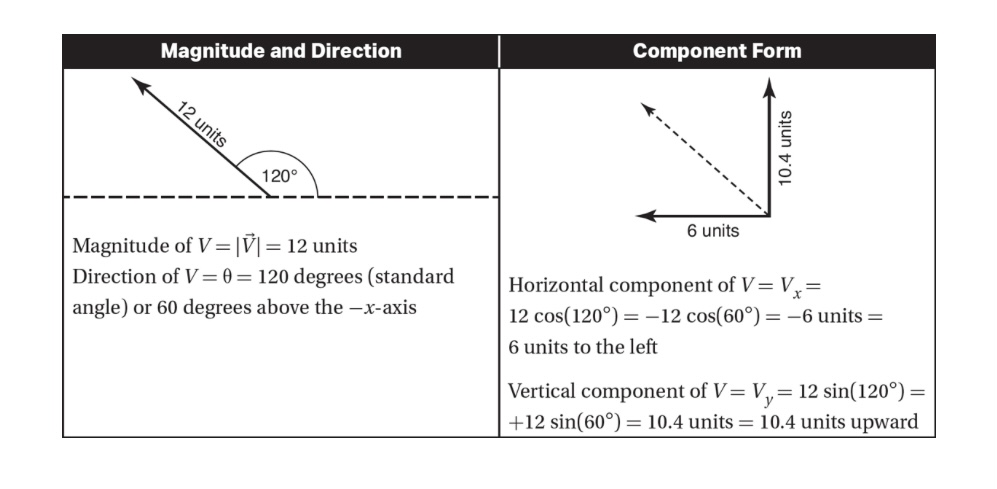
Here is an example of a vector described in two equivalent ways:
- MAGNITUDE AND DIRECTION: useful for drawing, visualizing and graphical analysis.
- COMPONENT FORM: useful for calculations and mathematical operations You must be able to use the math in this section to go back and forth between these two representations fluently.
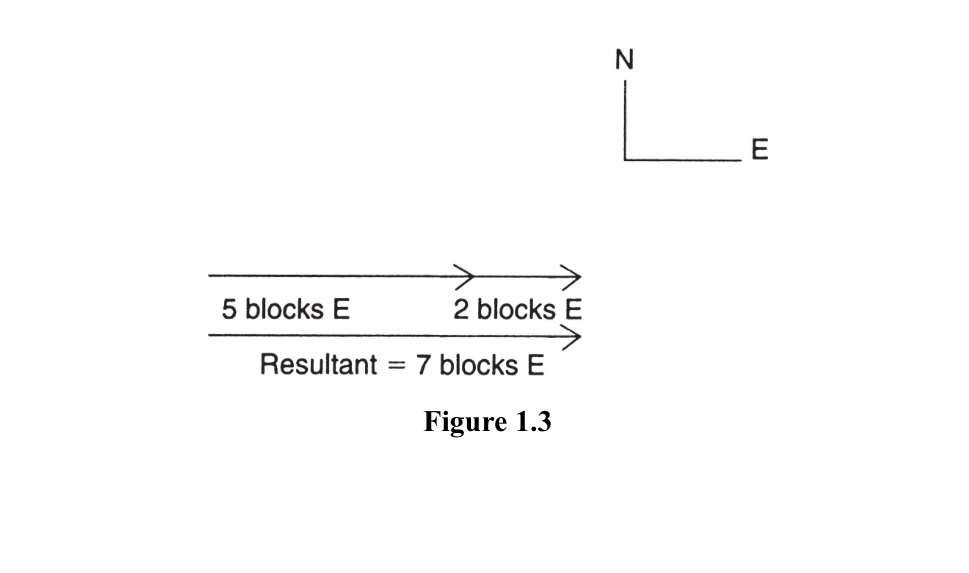
 Example 1
Example 1
First, suppose a girl is walking from her house a distance of five blocks east and then an additional two blocks east. How can we represent these displacements vectorially? First, we must choose a suitable scale to represent the magnitude lengths of the vectors. In this case, let us just call the scale "one vector unit" or just "one unit," to be equal to one block of distance. Let us also agree that "east" is to the right (and hence "north" is directed up). A vector diagram for this set of displacements is given in Figure 1.3. Note that the resultant has both magnitude and direction as it, too, is a vector.
Example 2
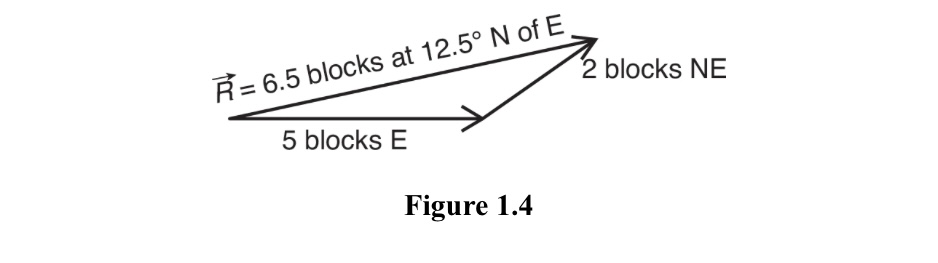
Now, for our second example, suppose the girl walks five blocks east and then two blocks northeast (that is, 45 degrees north of east). As before, we draw our vector diagram, using the same scale as before, so that the two vectors are connected "head to tail" or "tip to tail." The vector diagram will look like Figure 1.4. The resultant is drawn from the tail of the first vector to the head of the second, forming a triangle (some texts use the "parallelogram" method of construction, which is equivalent. The direction of the resultant is measured from the horizontal axis as usual.
The Addition of Vectors:
The addition of vectors involves combining vectors to find a resultant vector.
Vectors can be added graphically by placing the tail of one vector at the head of the other vector and drawing the resultant vector from the tail of the first vector to the head of the second vector.
The magnitude of the resultant vector can be found using the Pythagorean theorem, and the direction of the resultant vector can be found using trigonometry.
Vectors can also be added algebraically by adding the corresponding components of the vectors.
The addition of vectors is commutative, meaning that the order in which the vectors are added does not affect the result.
The addition of vectors is associative, meaning that the way that the vectors are grouped does not affect the result.
The addition of vectors can be used to find the net force acting on an object or the resultant velocity of an object moving in multiple directions.
The addition of vectors is a fundamental concept in physics and is used in many areas of mechanics, electromagnetism, and other fields.
Addition of Multiple Vectors
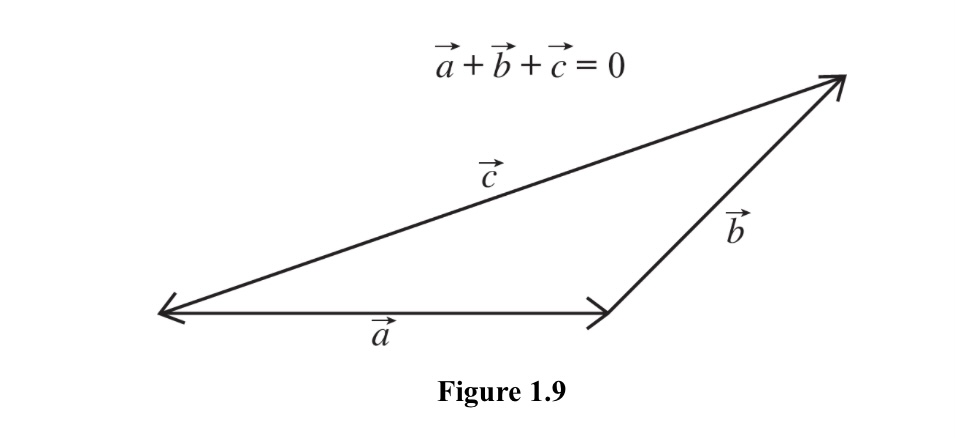
As long as the vectors are constructed head to tail, multiple vectors can be added in any order. If the resultant is zero, the diagram constructed will be a closed geometric figure. This can be shown in the case of three vectors forming a closed triangle, as in Figure 1.9.
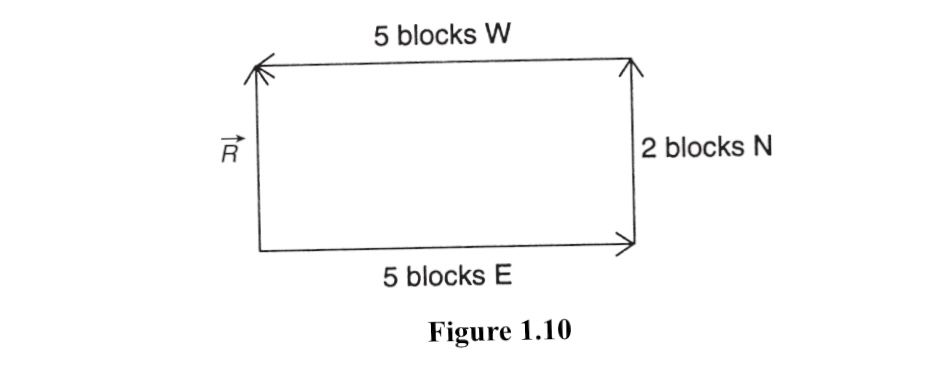
Thus, if the girl walks five blocks east, two blocks north, and five blocks west, the vector diagram will look like Figure 1.10, with the resultant displacement being equal to two blocks north.
- Addition Methods Using the Components of Vectors
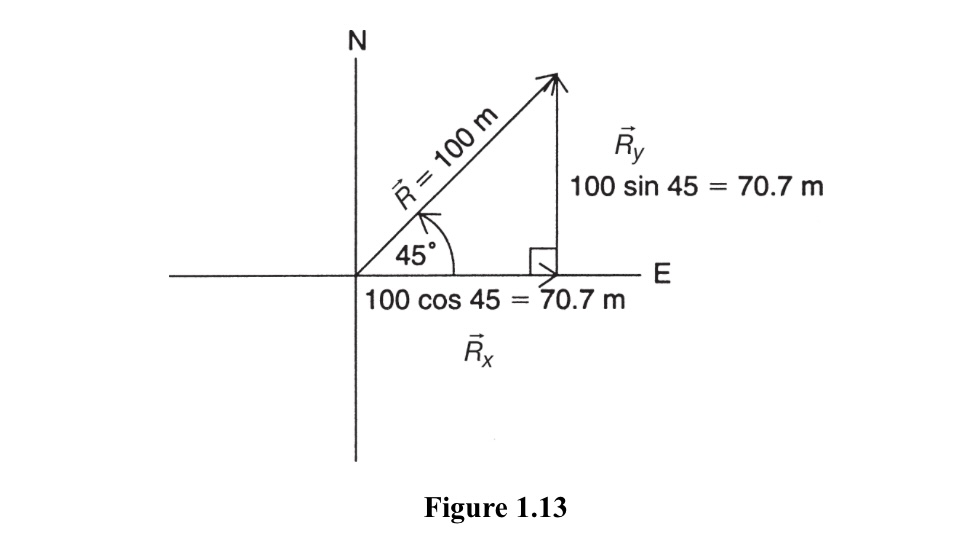
Any single vector in space can be resolved into two perpendicular components in a suitably chosen coordinate system. The methods of vector resolution were discussed at the beginning of this section, but we can review them here. Given a vector (sketched in Figure 1.13) representing a displacement of 100 meters northeast (that is, making a 45-degree angle with the positive x-axis), we can observe that it is composed of an x- and a y- (a horizontal and a vertical) component that can be geometrically or algebraically determined.
The Subtraction of Vectors:
The subtraction of vectors involves finding the difference between two vectors.
Vectors can be subtracted graphically by placing the tail of one vector at the head of the other vector and then drawing the resultant vector from the head of the first vector to the tail of the second vector.
The subtraction of vectors can also be performed algebraically by subtracting the corresponding components of the vectors.
The subtraction of vectors is not commutative, meaning that changing the order of the vectors changes the result.
Subtraction of Vectors
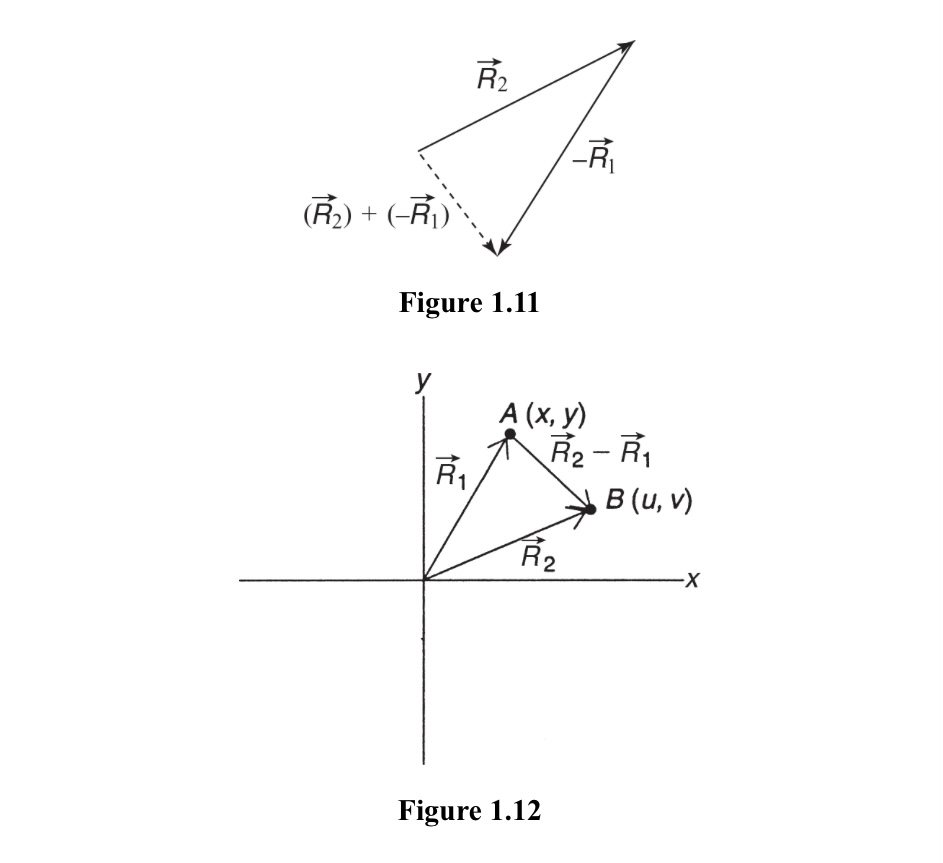
The subtraction of vectors is best understood by rethinking the subtraction as the addition of a negative vector.
R3 - R, = Rz+ (-R,)
A negative vector is simply one of the same magnitude but directed opposite (i.e., a 180-degree rotation). Note that the result of this operation is the same here as in the example that follows since the resultant has the same magnitude and direction. See Figures 1.11 and 1.12. This difference between the two vectors is sometimes called AR, so that AR = Ro- R,.
\n \n