Key Ideas

• The force on a moving charge due to a magnetic field is qvB..

• The direction of the magnetic force on a moving charge is given by a right-hand rule, and is NOT in the direction of the magnetic field.

• Current-carrying wires produce magnetic fields.

• When the magnetic flux through a wire changes, a voltage is induced.

• An inductor inhibits the change in the current running through it. After a long time, the inductor acts as a bare wire.

Magnetic Fields

• All magnets are dipoles, which means that they have two “poles,” or ends.

• Opposite poles attract, and like poles repel.

• A magnet creates a magnetic field.

• Magnetic field lines form loops.

• These loops point away from the north end of a magnet and toward the south end.

• Near the magnet, the lines point nearly straight into or out of the pole.

Long, Straight, Current-Carrying Wires

• Current-carrying wires also create magnetic fields.

• The magnetic field created by a long, straight, current-carrying wire loops around the wire in concentric circles.

• The direction in which the magnetic field lines loop is determined by a right-hand rule.

• To find the direction of the B field produced by long, straight, current-carrying wires:

  • Pretend you are holding the wire with your right hand. Point your thumb in the direction of the current.

  • Your fingers wrap around your thumb the same way that the magnetic field wraps around the wire.

• The formula that describes the magnitude of the magnetic field created by a long, straight, current-carrying wire is the following:

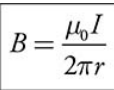
• B is the magnitude of the magnetic field.

• μ0 is a constant called the permeability of free space.

• I is the current flowing in the wire.

• r is the distance from the wire.

Moving Charged Particles

• A magnetic field exerts a force on a charged particle if that particle is moving perpendicular to the magnetic field.

• A magnetic field does not exert a force on a stationary charged particle, nor on a particle that is moving parallel to the magnetic field.

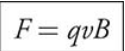
• The magnitude of the force exerted on the particle equals the charge on the particle, q, multiplied by the velocity of the particle, v, multiplied by the magnitude of the magnetic field

• Right-hand rule: To find the force on a charged particle.

  • Point your right hand, with fingers extended, in the direction that the charged particle is traveling. Then, bend your fingers so that they point in the direction of the magnetic field.

  • If the particle has a POSITIVE charge, your thumb points in the direction of the force exerted on it.

  • If the particle has a NEGATIVE charge, your thumb points opposite the direction of the force exerted on it.

• Acceleration is centripetal, and the particle must move in a circle at a constant speed.

• But even if the particle were speeding up at this rate, either the acceleration wouldn’t act for very long, or relativistic effects would prevent the particle from traveling faster than light.

Magnetic Force on a Wire

• A current is simply the flow of positive charges.

• If we put a current-carrying wire perpendicular to a magnetic field, we have placed moving charges perpendicular to the field, and these charges experience a force.

• The formula for the force on a long, straight, current-carrying wire in the presence of a magnetic field is

  

• The force on a wire equals the current in the wire, I.

• The length of the wire is L.

• The magnitude of the magnetic field is B.

Mass Spectrometry: More Charges Moving Through Magnetic Fields

• A magnetic field can make a charged particle travel in a circle.

  

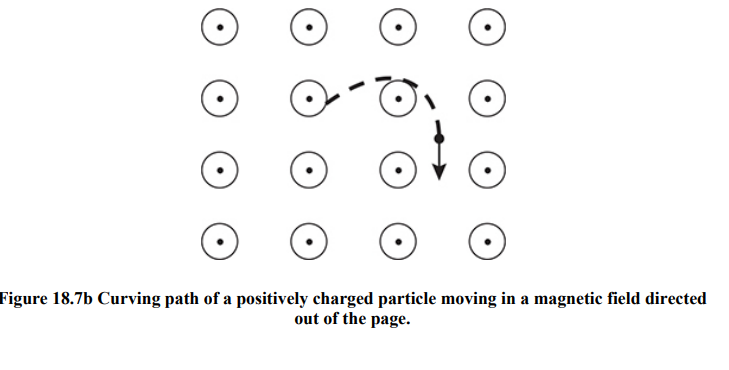
• The particle travels through a tiny opening and enters a uniform magnetic field.

• This magnetic field exerts a force on the particle, and the particle begins to travel in a circle.

Induced EMF

• A changing magnetic field produces a current. We call this occurrence electromagnetic induction.

• Induced EMF: The potential difference created by a changing magnetic field that causes a current to flow in a wire.

• Magnetic Flux: The number of magnetic field lines that pass through an area.

• The units of flux are called webers; 1 weber = 1 T·m2 . The equation for magnetic flux is:

  

• ΦB is the magnetic flux.

• B is the magnitude of the magnetic field.

• A is the area of the region that is penetrated by the magnetic field..

• A changing magnetic flux creates an induced EMF.

• Faraday’s Law tells us exactly how much EMF is induced by a changing magnetic flux.

  

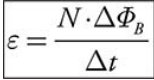
• ε is the induced EMF.

• N is the number of loops you have.

• Δt is the time during which your magnetic flux, ΦB , is changing.

• Lenz’s Law: States that the direction of the induced current opposes the increase in flux.

• When a current flows through a loop, that current creates a magnetic field.

  

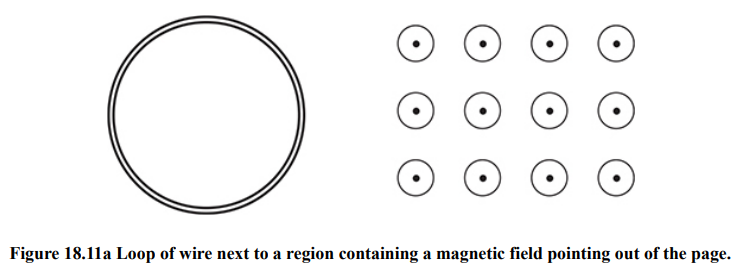
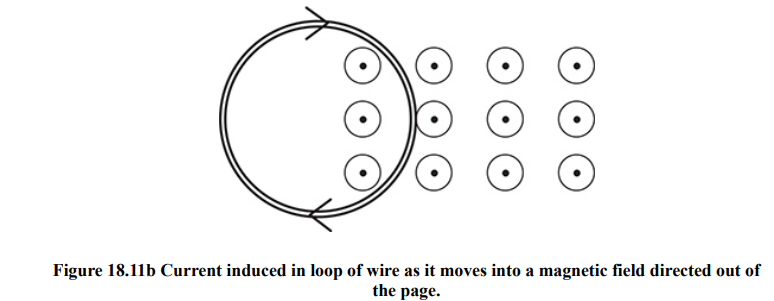
• To solve a problem that involves Lenz’s Law, use this method:

  • Point your right thumb in the initial direction of the magnetic field

  • “Is the flux increasing or decreasing?”

  • If the flux is decreasing, then just curl your fingers (with your thumb still pointed in the direction of the magnetic field). Your fingers show the direction of the induced current.

  • If the flux is increasing in the direction you’re pointing, then flux is decreasing in the other direction.

  • So, point your thumb in the opposite direction of the magnetic field, and curl your fingers. Your fingers show the direction of the induced current.

Induced EMF in a Rectangular Wire

• If we pull a rectangular wire into or out of a uniform field B at constant speed v, then the induced EMF in the wire is found by:

  

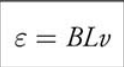
The Biot-Savart Law and Ampere’s Law

• The Biot-Savart Law provides a way to find the magnetic field produced by pretty much any type of current.

• A little element of wire carrying a current produces a magnetic field that

  • wraps around the current element via the right-hand rule, and

  • decreases in magnitude as 1/r 2, r being the distance from the current element

Ampere’s Law

• Ampere’s Law gives an alternative method for finding the magnetic field caused by a current.

• There are three important results of Ampere’s Law:

  • The magnetic field produced by a very long, straight current is

    

  • outside the wire; inside the wire, the field increases linearly from zero at the wire’s center.

  • A solenoid is set of wound wire loops.

    • A current-carrying solenoid produces a magnetic field.

    • Ampere’s Law can show that the magnetic field due to a solenoid is shaped like that of a bar magnet.

    • the magnitude of the magnetic field inside the solenoid is approximately uniform.

  • The magnetic field produced by a wire-wrapped torus is zero everywhere outside the torus, but nonzero within the torus. The direction of the field inside the torus is around the donut.

Maxwell Equations

• Maxwell equation 1 is simply Gauss’s Law: the net electric flux through a closed surface is proportional to the charge enclosed by that surface.

• Maxwell equation 2 is sometimes called Gauss’s Law for magnetism: the net magnetic flux through a closed surface must always be zero. The consequence of this equation is that magnetic poles come in north/south pairs—you cannot have an isolated north magnetic pole.

• Maxwell equation 3 is simply Faraday’s Law: a changing magnetic flux through a loop of wire induces an EMF.

• Maxwell equation 4 is partly Ampere’s Law, but with an addition called “displacement current” that allows the equation to be valid in all situations. The principal consequence is that just as a changing magnetic field can produce an electric field, a changing electric field can likewise produce a magnetic field.