Unit 1: Electrostatics
1.1: Electric Charge & Coulomb's Law
Charge
- Charge: It is a fundamental property of matter that describes the amount of electrical energy present in an object.
- It is a scalar quantity that can be either positive or negative.
- The SI unit of charge is Coulomb (C).
| Charge | Coulombs | Elementary Charge |
|---|---|---|
| +1 | 1.602 × 10^-19 C | 1 e |
| +2 | 3.204 × 10^-19 C | 2 e |
| +3 | 4.806 × 10^-19 C | 3 e |
| -1 | -1.602 × 10^-19 C | -1 e |
| -2 | -3.204 × 10^-19 C | -2 e |
| -3 | -4.806 × 10^-19 C | -3 e |
Electric Charge
- Electric charge: It is a fundamental property of matter that arises from the presence or absence of electrons in an atom.
- It can be positive or negative, and like charges repel while opposite charges attract.
- The unit of electric charge is the Coulomb (C), and the basic unit of charge is the electron, which has a charge of
-1.602 x 10^-19 C. - Electric charge plays a crucial role in many areas of physics, including electromagnetism and electrostatics. It is also the basis for the study of electric circuits and electronics.
Conservation of Charge
- The law of conservation of charge is a fundamental principle of physics and is applicable to all physical systems.
- It is closely related to the conservation of energy and momentum.
- The principle of conservation of charge is used in various fields of science, including electrostatics, electrodynamics, and quantum mechanics.
- The conservation of charge is a consequence of the symmetry of physical laws under the transformation of time.
- It is a fundamental principle of nature and has been experimentally verified to a high degree of accuracy.
- It is an important concept in the study of electricity and magnetism and is used to explain many phenomena, including the behavior of electric circuits and the interaction of charged particles with electromagnetic fields.
- It is a fundamental principle that underlies many of the technological advances of the modern world, including electronics, telecommunications, and power generation.
Conductors and Insulators
- Conductors: These are materials that allow electric charge to flow freely through them.
- Insulators: These are materials that do not allow electric charge to flow easily.
- Metals are good conductors, while materials such as rubber and plastic are good insulators.
Law of Electrostatics
- The law of electrostatics is a set of fundamental principles that govern the behavior of electric charges at rest.
- These laws are based on observations and experiments conducted by scientists over the years.
Coulomb's Law
- Coulomb's law: This law states that the force between two point charges is directly proportional to the product of their charges and inversely proportional to the square of the distance between them. Mathematically, it can be expressed as:
F = k * (q1 * q2) / r^2- where:
- F is the force between the charges
- q1 and q2 are the magnitudes of the charges
- r is the distance between them
- k is the Coulomb constant.
Electric Field
- Electric field: A region in space where an electric charge experiences a force.
- The strength of the electric field at a point is defined as the force per unit charge acting on a test charge placed at that point. Mathematically, it can be expressed as:
E = F / q- where:
- E is the electric field strength
- F is the force acting on the test charge
- q is the magnitude of the test charge.
Electric Potential
- Electric potential: It is the amount of work required to move a unit charge from one point to another in an electric field. It is measured in volts (V) and is defined as:
V = W / q- where:
- V is the electric potential
- W is the work done in moving the charge
- q is the magnitude of the charge.
Electric Potential Difference
- Electric potential difference is the difference in electric potential between two points in an electric field. It is measured in volts (V) and is defined as:
ΔV = V2 - V1- where:
- ΔV is the electric potential difference
- V1 is the electric potential at point 1
- V2 is the electric potential at point 2.
Charging and Discharging
- Charging
- Charging: It is the process of adding electrical energy to a system.
- In the case of a battery, charging involves applying an external voltage to the battery terminals, which causes a chemical reaction that stores energy in the battery.
- The charging process is typically slower than discharging, as it involves a chemical reaction that takes time to complete.
- Overcharging a battery can cause damage or even lead to a fire or explosion, so it's important to use a charger that is designed for the specific type of battery being charged.
- Discharging
- Discharging: It is the process of releasing electrical energy from a system.
- In the case of a battery, discharging involves allowing the stored energy to flow out of the battery and into a load, such as a light bulb or motor.
- The rate of discharge depends on the load connected to the battery and the capacity of the battery itself.
- Discharging a battery too quickly can cause it to overheat and potentially fail, so it's important to use a load that is appropriate for the battery's capacity.
Electrostatic Force & Coulomb's Law
Electrostatic force is the force that exists between electrically charged particles. This force can be either attractive or repulsive, depending on the charges of the particles. The strength of the electrostatic force is determined by Coulomb's Law. The equation for calculating electrostatic force is:
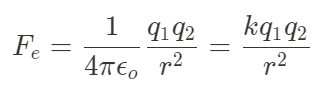
Coulomb's Law states that the electrostatic force between two charged particles is directly proportional to the product of their charges and inversely proportional to the square of the distance between them. The mathematical expression for Coulomb's Law is:
F = k * (q1 * q2) / r^2- where:
- F is the electrostatic force
- q1 and q2 are the charges of the particles
- r is the distance between them
- k is Coulomb's constant.
Coulomb's constant is a proportionality constant that depends on the medium between the charged particles.
In a vacuum, Coulomb's constant has a value of approximately
9 x 10^9 N*m^2/C^2.The electrostatic force between two charged particles can be attractive or repulsive, depending on the signs of their charges.
Like charges (positive and positive, or negative and negative) repel each other, while opposite charges (positive and negative) attract each other.
1.2: Electric Fields & Electric Potential
Electric Fields
- An electric field is a vector field that describes the force exerted on a charged particle by other charged particles.
- The electric field is defined as the force per unit charge that a test charge would experience if placed in the field.
Rules for Drawing Electric Fields
- Electric field lines always start on positive charges and end on negative charges.
- The number of electric field lines leaving a positive charge or entering a negative charge is proportional to the magnitude of the charge.
- Electric field lines never cross each other.
- Electric field lines are always perpendicular to the surface of a conductor.
- The density of electric field lines is proportional to the strength of the electric field.
Electric Field Strength
Electric field strength is the force per unit charge experienced by a test charge placed in an electric field. It is a vector quantity and is denoted by E.
The electric field strength at a point in an electric field is given by the formula:
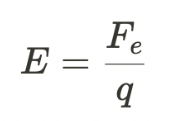
- where:
- E is the electric field strength
- F is the force experienced by the test charge
- q is the magnitude of the test charge.
The SI unit of electric field strength is newtons per coulomb (N/C).
The direction of the electric field strength is the direction of the force experienced by a positive test charge placed in the electric field.
Electric Field Strength due to a Point Charge
- The electric field strength due to a point charge is given by Coulomb's law:
E = k * Q / r^2- where:
- E is the electric field strength
- k is Coulomb's constant
- Q is the magnitude of the point charge
- r is the distance between the point charge and the test charge.
Electric Field Strength due to a Uniformly Charged Sphere
- The electric field strength due to a uniformly charged sphere at a point outside the sphere is given by:
E = k * Q / r^2- where:
- E is the electric field strength
- k is Coulomb's constant
- Q is the total charge on the sphere
- r is the distance between the center of the sphere and the test charge.
- Inside the sphere, the electric field strength is given by:
E = k * Q * r / R^3- where:
- R is the radius of the sphere
- r is the distance between the center of the sphere and the test charge.
Electric Fields in Conductors
- In a conductor, electric charges are free to move.
- When an electric field is applied to a conductor, the charges will move until they reach a state of equilibrium.
- The electric field inside a conductor is zero, as the charges will continue to move until the electric field is cancelled out.
- Any excess charge on a conductor will reside on its surface, as the charges repel each other and move as far away from each other as possible.
- The electric field just outside the surface of a conductor is perpendicular to the surface and proportional to the surface charge density.
Electric Fields in Insulators
- In an insulator, electric charges are not free to move.
- When an electric field is applied to an insulator, the charges will not move, but the atoms and molecules will become polarized.
- The electric field inside an insulator is not zero, as the charges are not free to move and will experience a force.
- The electric field just outside the surface of an insulator is perpendicular to the surface and proportional to the surface charge density, similar to a conductor.
1.3: Point Charges - Fields & Potentials
Work Done by Electric Fields
- Electric fields can do work on charged particles.
- Work is done when a force moves an object over a distance.
- The work done by an electric field on a charged particle is given by the equation W = qEd, where W is the work done, q is the charge of the particle, E is the strength of the electric field, and d is the distance the particle is moved.
Applications of Electric Fields & Work
- Electric fields and work are used in many applications, such as:
- Capacitors: devices that store electric charge and energy.
- Electric motors: devices that convert electrical energy into mechanical energy.
- Particle accelerators: devices that use electric fields to accelerate charged particles to high speeds.
- Electrostatic precipitators: devices that use electric fields to remove pollutants from the air.
Electric Potential Energy
Electric potential energy: It is the energy that a charged particle possesses due to its position in an electric field. It is defined as the amount of work required to move a charged particle from infinity to a point in the electric field.
The SI unit of electric potential energy is joule (J).
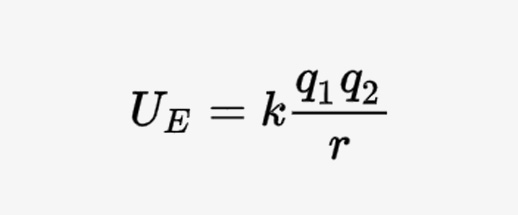
- where ∆Ue is the change in Electric Potential Energy.
Potential Difference
- Potential difference: It is the difference in electric potential energy per unit charge between two points in an electric circuit.
- It is also known as voltage and is measured in volts (V).
Electric Potential of a Point Charge
- The electric potential at a point in space is the amount of work required to bring a unit positive charge from infinity to that point.
- The electric potential of a point charge is given by:
V = kq/r- where:
- V is the electric potential
- k is Coulomb's constant
- q is the charge of the point charge
- r is the distance between the point charge and the point where the electric potential is being calculated.
- Some key points to note about the electric potential of a point charge are:
- The electric potential at infinity is zero.
- The electric potential is a scalar quantity and is measured in volts (V).
- The electric potential is a function of distance from the point charge and decreases as the distance increases.
- The electric potential is positive for a positive point charge and negative for a negative point charge.
- The electric potential can be used to calculate the electric field at any point in space. The electric field is given by:
E = -∇V- where:
- E is the electric field
- ∇ is the gradient operator.
- The negative sign indicates that the electric field points in the direction of decreasing electric potential.
1.4: Gauss' Law
Gauss' Law is a fundamental principle in electromagnetism that relates the electric flux through a closed surface to the charge enclosed within that surface. It is named after the German mathematician and physicist Carl Friedrich Gauss.
The statement of Gauss' Law is as follows:
- The electric flux through any closed surface is proportional to the charge enclosed within that surface.
In mathematical terms, this can be expressed as:
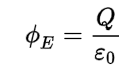
- where:
- ∮E⋅dA is the electric flux through a closed surface
- Q is the charge enclosed within that surface
- ε0 is the permittivity of free space.
Gauss' Law has many important applications in electromagnetism, including:
- Calculating the electric field due to a charged object or distribution of charges
- Determining the charge distribution within a conductor
- Analyzing the behavior of electric fields in dielectric materials
- Understanding the behavior of electric fields near conductors and insulators
Flux
- Flux is the amount of a physical quantity passing through a given surface.
- In electrostatics, electric flux is the measure of the electric field passing through a given surface.
- Mathematically, electric flux can be expressed as:
Φ = ∫E ⋅ dA- where,
- Φ is the electric flux through a surface,
- E is the electric field, and
- dA is the area vector of the surface.
Gauss's Law Flux Sample Problem
A point charge of +2 nC is located at the center of a sphere of radius 10 cm. Find the electric flux through the surface of the sphere.
Solution
- We can use Gauss's law to solve this problem. Gauss's law states that the electric flux through a closed surface is proportional to the charge enclosed within the surface. Mathematically, it can be written as:
Φ = Q / ε₀- where Φ is the electric flux, Q is the charge enclosed within the surface, and ε₀ is the permittivity of free space.
- In this problem, the charge enclosed within the surface is the point charge of +2 nC. Therefore, we can write:
Q = +2 nC- The surface in this problem is a sphere of radius 10 cm. We can choose a Gaussian surface that is also a sphere of radius 10 cm. Since the point charge is located at the center of the sphere, the electric field is radial and has the same magnitude at every point on the Gaussian surface.
- Using the formula for the electric field due to a point charge, we can find the magnitude of the electric field at the surface of the Gaussian sphere:
E = kQ / r²- where k is Coulomb's constant, Q is the point charge, and r is the radius of the Gaussian sphere.
- Substituting the given values, we get:
E = (9 × 10^9 Nm²/C²) × (2 × 10^-9 C) / (0.1 m)²E = 36 N/C
- The electric flux through the Gaussian surface is then:
Φ = E × A- where A is the area of the Gaussian surface. Since the Gaussian surface is a sphere, its area is:
A = 4πr²
- Substituting the given values, we get:
A = 4π × (0.1 m)²A = 0.04π m²
- Therefore, the electric flux through the surface of the sphere is:
Φ = (36 N/C) × (0.04π m²)Φ = 4.52 Nm²/C
1.5: Other Charge Distributions - Fields & Potentials
Extended Charge Distributions
- Extended charge distributions: This refer to the distribution of electric charge over a three-dimensional object.
- The electric field produced by an extended charge distribution can be calculated using Coulomb's law, but the calculation is more complex than for a point charge.
- Continuous Charge Distributions
- These charge distributions are those where the charge is distributed continuously over a volume or surface.
- The charge density, which is the amount of charge per unit volume or unit area, is used to describe the distribution.
- The electric field produced by a continuous charge distribution can be calculated using integration.
- Spherical Charge Distributions
- These charge distributions are those where the charge is distributed uniformly over the surface of a sphere.
- The electric field produced by a spherical charge distribution can be calculated using Gauss's law, which relates the electric flux through a closed surface to the charge enclosed within the surface.
- Cylindrical Charge Distributions
- These charge distributions are those where the charge is distributed uniformly over the surface of a cylinder.
- The electric field produced by a cylindrical charge distribution can also be calculated using Gauss's law.
- Planar Charge Distributions
- These charge distributions are those where the charge is distributed uniformly over a flat surface.
- The electric field produced by a planar charge distribution can be calculated using Coulomb's law, but the calculation is simplified by assuming that the surface is infinite and the charge is distributed uniformly.
Gauss' Law for Various Shapes
| Line of Charge | 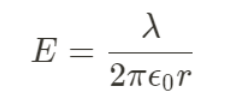 |
|---|---|
| Point, Hoop, or Sphere | 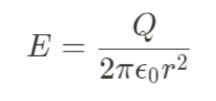 |
| Sphere | 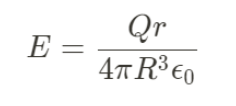 |
| Insulating Sheet of Charge | 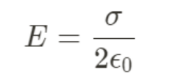 |