Honors Chem Unit 2 notes (For Allen)
Types of Bonding
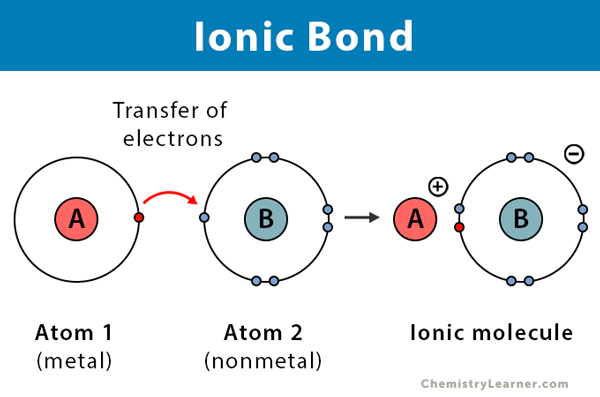
Ionic Bonding
Occurs when there is a large electronegativity difference between two atoms, typically between a metal and a nonmetal.
Involves the complete transfer of one or more valence electrons from one atom (the metal, forming a cation) to another (the nonmetal, forming an anion).
The electrostatic attraction between the oppositely charged ions holds the compound together.
Examples: Sodium chloride (NaCl), Magnesium oxide (MgO).
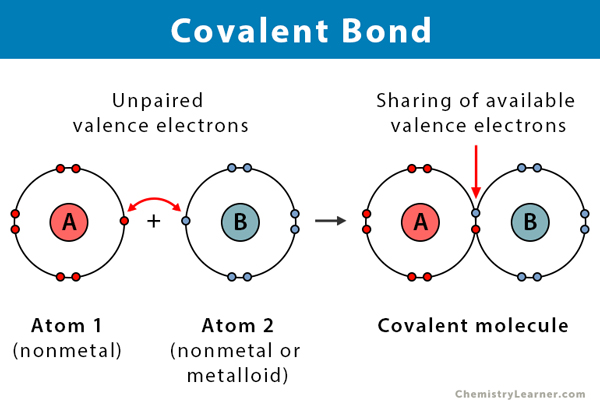
Covalent Bonding
Occurs when two atoms share one or more pairs of valence electrons.
Typically found between two nonmetal atoms.
Can be classified into:
Nonpolar Covalent Bond: Electrons are shared equally between atoms (e.g., O2O2, H2H2).
Polar Covalent Bond: Electrons are shared unequally due to a difference in electronegativity, creating partial positive (δ+δ+) and partial negative (δ−δ−) charges on the atoms (e.g., Water (H2OH2O), Hydrogen chloride (HCl)).
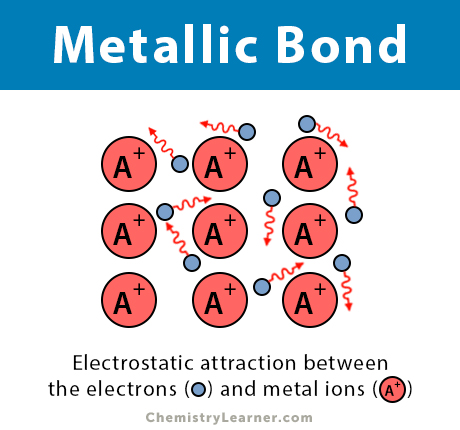
Metallic Bonding
Occurs in metals, where a "sea" of delocalized valence electrons is shared among a lattice of positively charged metal ions.
The electrons are not associated with any single atom or bond but are free to move throughout the structure.
This type of bonding accounts for many characteristic properties of metals, such as electrical conductivity, thermal conductivity, malleability, and ductility.
Examples: Copper (Cu), Iron (Fe), Gold (Au).
Physical vs Chemical Properties
Physical Properties
Physical properties can be observed or measured without changing the substance's chemical identity.
Examples include color, density, melting point, boiling point, and hardness.
Chemical Properties
Chemical properties describe how a substance reacts with other substances, resulting in a change in its chemical composition.
Examples include flammability, reactivity with acids, and oxidation.
Intensive vs Extensive Properties
Intensive Properties
Intensive Properties do not depend on the amount of matter in an object.
Examples include temperature, boiling point, and lustre.
Extensive Properties
Properties that change with the amount of matter. Examples include weight, length, and volume.
Measurements
Accuracy
A measure of how close the measured value is compared to the actual value.
Precision
A measurement of how close measurements are to each other.
Tools for measurements
Graduated Cylinder
Buret
Electric Balance
Meter Stick
Measurements cannot be more precise than the equipment used, as every piece of equipment has a degree of precision, which is defined by the smallest marked measurement.
When measuring liquid with a graduated cylinder, measure from the meniscus (the small dip at the top of the pool).

Degree of Uncertainty
You can estimate one digit past the degree of precision, which is called the Degree of Uncertainty. Chemical PropertiesChemical Properties
Significant Figures (Sig Figs)
What are Sig Figs?
A way to report numbers as accurately as possible.
Finding Sig Figs
If the decimal point is Present, you cross out the Zeros and stops at the first non-zero digit, from LEFT TO RIGHT (Example, 0.0000183, 3 sig figs)
If the decimal point is Absent, you cross out the Zeros and stop at the first non-zero digit, from RIGHT TO LEFT (Example, 18200000, 3 sig figs)
To find the Sig Figs in a number, you count the remaining digits in the number.
When crossing out the zeros, DO NOT start from the decimal point, start from the Right or Left of the actual
number.
Numbers where you don't count the Sig Figs
Exact numbers (Certain Values, like "like there are 5 chairs in this room“); they have infinite sig figs
Counting numbers; Similar to exact numbers
Conversion Numbers: 100.000… cm - 1.000 m
Integral Numbers (Numbers that are certain parts of an equation); Diameter/2 ←This won't have Sig Figs
Addition and Subtraction
The answer should have the same number of decimal places as the least number of places in the equation.
Ex. 100.1 + 356.25 = 456.35 → 456.4
Ex. 636.421 - 212.16 = 424.261 → 424.26
You should round up to satisfy this rule.
Multiplication and Division
The answer should have the same number of Sig Figs as the number with the fewest Sig Figs.
Ex. 300.2 (4 sigs) \cdot 12.1 (3 sigs, you want this one) = 3632.42 → 3630 (3 sigs)
Ex. 256.8 (4 sigs) / 32.5 (3 sigs, you want this one) = 68.48 → 68.5 (3 sigs)
Mixed Operations
Switch between the rules
Ex. 0.556 \cdot (40 - 32.5) = 4.17 → 4.2
Scientific Notation
Scientific notation of the abbreviation of numbers with a large number of digits.
Basic Rules:
The coefficient has to be between 1-9.99
The coefficient has to be multiplied by a base of 10
The exponent must reflect the movement of the decimal.
If the exponent is positive, the movement of the decimal is to the right;
if it is negative, the movement is to the left.

Mass, Volume, and Density
Mass
How much matter is in an object
Measured in grams usually
Volume
How much space is filled by the matter of an object
Measured in either mL or cm3 usually
1 mL is equal to 1 cm3
Water Displacement
How much matter is in an object
Density
Amount of Mass in a set space.
Measured in the unit of Mass over the unit of Volume.
Water Displacement
If an item has a density less than the liquid it is in, then it will float
If an item has a density greater than the liquid it is in, then it will not float
If an item has a density equal to the liquid it is in, then it will neither float nor sink
Formulas to find Mass, Volume, or Density
Density; D=\frac{M}{V}
Mass; M=D\cdot V
Volume; V
=\frac{M}{D}
Density Graphs
Remember y=mx+b? You PROBABLY SHOULD!!!!
The y is the mass of an object, the x is the volume, and the slope (m) is the density!!!!
THIS WILL PROBABLY BE ON THE TEST SO LEARN THIS PROBABLY
NOW DO THE EXTRA PRACTICE
I'm going to become a statistic soon……………