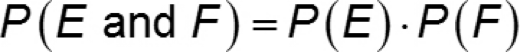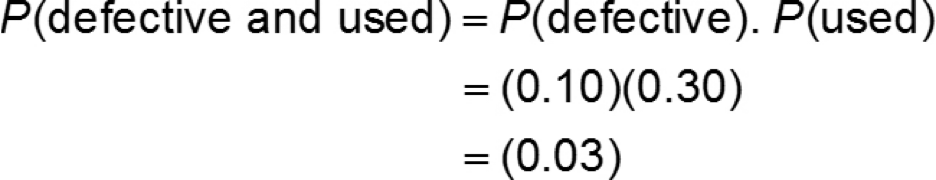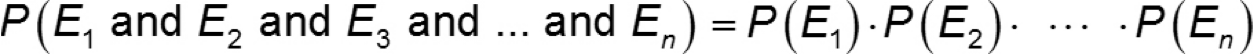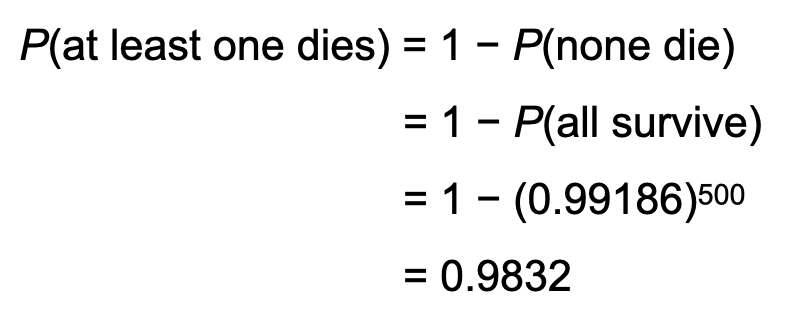Learning Objectives:

1. Identify independent events

2. Use the Multiplication Rule for Independent Events

3. Compute at-least probabilities

The Criteria: When is an Event independent or dependent?

• Two events E and F are independent if..

  • the occurrence of event E in a probability experiment does not affect the probability of event F.

• Two events are dependent if…

  • the occurrence of event E in a probability experiment does affect the probability of event F.

EXAMPLE Independent or Not?

1. Suppose you draw a card from a standard 52-card deck of cards and then roll a die. Are the events “draw a heart” and “roll an even number” independent or dependent?

   • Independent because the results of choosing a card do not impact the results of the die toss.

2. Suppose two 40-year old women who live in the United States are randomly selected. Are the events “woman 1 survives the year” and “woman 2 survives the year” independent or dependent?

   • Independent because

3. Suppose two 40-year old women live in the same apartment complex. Are the events “woman 1 survives the year” and “woman 2 survives the year” independent or dependent?

   • Independent because

Multiplication Rule for Independent Events

If E and F are independent events, then

EXAMPLE Computing Probabilities of Independent Events

The probability that a randomly selected female aged 60 years old will survive the year is 99.186% according to the National Vital Statistics Report, Vol. 47, No. 28.

• What is the probability that two randomly selected 60 year old females will survive the year?

  • The survival of the first female is independent of the survival of the second female. We also have that P(survive) = 0.99186.

    • 

EXAMPLE Computing Probabilities of Independent Events

A manufacturer of exercise equipment knows that 10% of their products are defective. They also know that only 30% of their customers will actually use the equipment in the first year after it is purchased.

• If there is a one-year warranty on the equipment, what proportion of the customers will actually make a valid warranty claim? 

  • We assume that the defectiveness of the equipment is independent of the use of the equipment. So,

    • 

Multiplication Rule for Multiple (n) Independent Events

If E₁, E₂, E₃, … and E_n are independent events, then

EXAMPLE Illustrating the Multiplication Principle for Independent Events

The probability that a randomly selected female aged 60 years old will survive the year is 99.186% according to the National Vital Statistics Report, Vol. 47, No. 28.

• What is the probability that four randomly selected 60 year old females will survive the year?

  • P(all 4 survive) is P(1^st survives and 2^nd survives and 3^rd survives and 4^th survives)

    = P(1^st survives) • P(2^nd survives) • P(3^rd survives) • P(4^th survives)

    = (0.99186) (0.99186) (0.99186) (0.99186)  

    = 0.9678

“At least” Rule for Probabilities

• calculate the probability of the complementary event (i.e., the event occurring zero times) and then subtracting that value from 1. 

  • P(at least one event) = 1 - P(none of the events) 

EXAMPLE Computing “at least” Probabilities

The probability that a randomly selected female aged 60 years old will survive the year is 99.186% according to the National Vital Statistics Report, Vol. 47, No. 28.

• What is the probability that at least one of 500 randomly selected 60 year old females will die during the course of the year?

  • 

Solution:

• Convert the value of x to a z-score. Use Table V to find the row and column that correspond to z. The area to the left of x is the value where the row and column intersect.

• Use technology to find the area.