OLI - 3. Semantics
Truth-value assignments
- Our primary interest in sentential logic has to do with the truth-values of formulae.
- The syntactic rules allow us to determine whether or not an expression constitutes a well-formed formula.
- Semantic rules allow us to determine the truth-value of any formula.
- If we don't know the truth-values of all the atomic formulae we can still determine what the truth-value of the formula will be for any possible assignment of truth-values to atomic formulae.
- A truth-value assignment specifies a unique truth-value (either T or F) for each atomic formula.
- The truth-value of a compound formula is a function of the truth-values of its parts, a function determined by the formula's main connective.
- The connectives are truth-functional.
Truth-functions
- We can use truth-tables to represent truth-functions.
- If a truth-table doesn't mention a specific formulae, it is called a characteristic truth-table.
| p | q | & | v | → | ↔ |
|---|---|---|---|---|---|
| T | T | T | T | V | V |
| T | F | F | T | F | F |
| F | T | F | T | V | F |
| F | F | F | F | V | V |
Truth-definition
We can chase truth up the parse tree of a given formula, matching rows of the truth-tables to applications of syntactic rules in the tree.
- Replace the atomic formulae in the parse tree with the truth-values assigned to each.
Truth and falsity relative to a truth-value assignment
- If φ is an atomic formula (sentential letter) of sentential logic, then φ is true on σ∗ just in case σ assigns the value T to φ, and false otherwise.
- If φ is a formula of the form ¬ψ, then φ is true on σ∗ just in case ψ is false on σ∗, and false otherwise.
- If φ is a formula of the form (ψ&ρ), then φ is true on σ∗ just in case both ψ and ρ are true on σ∗, and false otherwise.
- If φ is a formula of the form (ψ∨ρ), then φ is true on σ∗ just in case either ψ is true on σ∗ or ρ is true on σ∗, and false otherwise.
- If φ is a formula of the form (ψ→ρ), then φ is true on σ∗ just in case either ψ is false on σ∗ or ρ is true on σ∗, and false otherwise.
Logical notions
- Tautology: if it is true on every truth-value assignment.
- Contradictory: if it is false on every truth-value assignment.
- Contingent: if it is true on some truth-value assignments, and false on others.
- Logical consequence: the conclusion of an argument is a logical consequence of its premises if and only if any truth-value assignment that makes all the premises true also makes the conclusion true.
- Validity: an argument is valid if and only if its conclusion is a logical consequence of its premises.
- Invalidity: an argument is invalid in case it is not valid. If there is some truth-value assignment that makes the premises true, but the conclusion false.
- Counterexample: a truth-value assignment that makes the premises of an argument true and its conclusion false.
- Conditional analogue: the conditional analogue of an argument with premises φ1,…,φn and conclusion χ is the formula ((φ1&(…&φn))→χ).
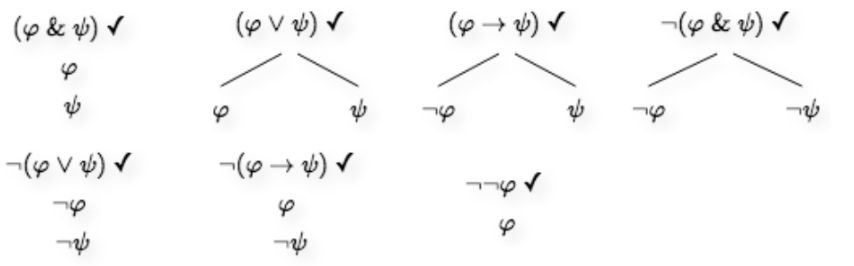
Truth-trees
The big difference is that while we make use of the syntactic rules when constructing parse trees, we will use the definition of truth with respect to a truth-value assignment in order to construct truth-trees.
Rules:
To construct them:
- Start by writing down the formula for which you want to generate a truth-tree.
- Based on the syntactic form of the expression, apply the appropriate truth-tree rule, putting a check mark next to the formula to indicate that it has been analyzed.
- For each open branch, determine whether the branch contains both any formula φ and its negation ¬φ. If any branch does contain a formula and its negation, mark the branch closed. If all branches in the tree are closed, you are done. Otherwise, continue to the next step.
- If the only formulae on open branches that do not have check marks next to them are atomic formulae or negations of atomic formulae, you are done. Otherwise, continue to the next step.
- Choose an unchecked formula on an open branch in the truth-tree that is not atomic and not the negation of an atomic formula, and apply this procedure to that formula, starting with step 2
A closed branch is marked with an asterisk, it doesn't represent any possible truth-value assignment.
- A branch that is not closed is open.
- An open branch is completed once no further decomposition rules can be applied.
- A tree is complete once every branch is complete.
Summary
- The basic notion of the semantics of sentential logic, the truth-value assignment, is introduced.
- The truth-functions embodied by the four logical connectives are introduced, and their role in determining the truth-value of a formula on a given truth-value assignment in discussed.
- The definition of truth relative to a given truth-value assignment is presented, and the construction of truth-tables is discussed.
- The semantic classifications of tautology, contingent, and contradictory are introduced, and definitions of the concepts of validity, invalidity, logical consequence, and counterexamples are given. The use of truth-tables in classifying and analyzing formulae and arguments is demonstrated.
- The notion of a truth-tree is introduced, and the use of truth-trees in semantically analyzing formulae and arguments is discussed, with emphasis on finding counterexamples.
New terms
| truth-values | truth-functional | function | truth-tables | truth-conditions |
|---|---|---|---|---|
| characteristic truth-table | LogicLab | logically true | contradictory | logical consequence |
| validity | invalidity | counterexample | truth-trees | closed branch |
| open branch | completed branch | completed truth-tree |
Definitions
- truth-value assignment
- characteristic truth-table for conjunction, disjunction, conditional and negation
- truth and falsity relative to a truth-value assignment
- tautology
- contradictory
- contingent
- logical consequence
- validity
- invalidity
- counterexample
- conditional analogue
- truth-tree construction rules
- truth tree: closed branch
- truth tree: open branch
- truth tree: completed branch
- completed truth tree
- procedure for generating truth-trees
- conditional analogue