Physics Notes
SEMESTER ONE SOPHOMORE PHYSICS:
Newton's Laws of Motion
First Law (Law of Inertia):
Definition: An object at rest remains at rest, and an object in motion continues moving with constant velocity unless acted upon by a net external force.
Implication: This law implies that in the absence of force, there will be no change in the object's motion.
Examples:
A book lying on a table stays there until someone pushes it.
An astronaut floating in space with no external forces will keep moving in the same direction.
Second Law:
Definition: The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass.
Formula: F = ma
F: Force (in Newtons, N)
m: Mass (in kilograms, kg)
a: Acceleration (in meters per second squared, m/s²)
Examples:
A 10 kg object experiencing a force of 20 N will have an acceleration of 2 m/s² (F = ma).
In sports, players apply force to accelerate their mass (e.g., a sprinter pushing off the ground).
Third Law:
Definition: For every action, there is an equal and opposite reaction.
Examples:
When jumping off a boat, you push the boat backward while you move forward.
A rocket propelling itself upward: the exhaust gases push down, and the rocket moves up.
Relative Motions and Frames of Reference
Frame of Reference:
Definition: A system for specifying the precise location of objects in space and time.
Types:
Inertial Frames: Non-accelerating frames, where Newton's laws hold.
Non-inertial Frames: Accelerating frames, where fictitious forces may need to be considered.
Example: Observing a car's motion from a moving train versus from the ground.
Relative Motion:
Concept: The motion of an object can appear different depending on the observer's frame of reference.
Implementation: Calculate motion by taking into account the velocities of multiple moving objects.
Examples:
A person walking on a train appears to the observer on the train to be stationary, while they appear to be moving to someone on the ground.
Newton's Law of Universal Gravitation
Law:
Definition: Every particle attracts every other particle with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers.
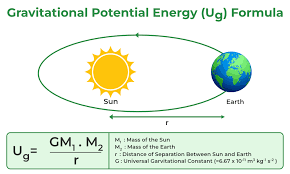
Formula: F = G (m₁m₂) / r²
F: Gravitational force (N)
G: Gravitational constant (6.674 × 10⁻¹¹ N(m/kg)²)
m₁, m₂: Masses of the two objects (kg)
r: Distance between the centers of the two masses (m)
Examples:
Calculating the gravitational force between Earth and an object:
If a 1 kg object is at the surface of Earth, the force can be calculated using Earth's mass and radius.
Newton's Second Law Calculation
Overview: Essential for analyzing forces and motion quantitatively.
Calculating Force:
Use F = ma to find the net force acting on an object.
Example:
A car with a mass of 1000 kg accelerating at 3 m/s² would experience a force of 3000 N (F = 1000 kg × 3 m/s²).
Setting Up Problems:
Identify all forces acting on the object.
Determine the net force by vector addition.
Apply the second law to find acceleration or mass accordingly.
Kinematics Introduction
Kinematics:
Definition: The study of the geometric aspects of motion, describing how objects move.
Key Variables:
Displacement: The vector quantity representing the change in position (m).
Velocity: The rate of change of displacement; can be average or instantaneous (m/s).
Acceleration: The rate of change of velocity (m/s²).
Types of Motion:
Linear Motion: Motion along a straight path.
Rotational Motion: Motion around an axis.
Kinematics Graphing
Graph Types:
Position-Time Graphs:
Shows the position of an object relative to time.
Slope indicated velocity (steeper slope = higher velocity).
Horizontal line indicates the object at rest.
Velocity-Time Graphs:
Represents how an object's velocity changes over time.
Slope indicates acceleration (positive slope = speeding up; negative slope = slowing down).
Area under the curve represents total displacement.
Acceleration-Time Graphs:
Shows how acceleration varies over time.
Flat lines indicate constant acceleration, while changes in line indicate varying acceleration.
Motion in Two Dimensions
Two-Dimensional Vector Addition:
Vector Components: Break down vectors into horizontal (x) and vertical (y) components.
Resultant Vector: The vector obtained by combining all the component vectors using Pythagorean theorem and trigonometric functions.
Example:
A vector 5 m east and a vector 3 m north can be combined:
Resultant = √(5² + 3²) m = 5.83 m at an angle of θ = tan⁻¹(3/5).
Projectile Motion:
Characteristics: A type of motion experienced by an object or particle that is thrown near the earth's surface and moves along a curved trajectory under the action of gravity.
Two Components:
Horizontal Motion: Uniform motion; horizontal velocity is constant.
Vertical Motion: Accelerated motion due to gravity, with an acceleration of approximately 9.81 m/s² downward.
Equations:
Horizontal Range: R = (v₀² * sin(2θ)) / g
Maximum Height: H = (v₀² * (sin²θ)) / (2g)
Solving a Quadratic Equation
Methods:
Factoring:
When possible, express the quadratic equation in the form (x - p)(x - q) = 0 and solve for x as p and q.
Quadratic Formula:
For any quadratic equation in the standard form ax² + bx + c = 0, use:
x = (-b ± √(b² - 4ac)) / (2a)
This gives two solutions for x.
Example: For 2x² - 4x - 6 = 0, a = 2, b = -4, c = -6, so calculate using the quadratic formula.
Completing the Square:
Rearranging the equation to form a perfect square trinomial, enabling easy solution extraction.
Useful for deriving the quadratic formula and understanding the vertex form of parabolas.
Nuclear Decay Notes
Definition: A process by which an unstable atomic nucleus loses energy by emitting radiation, leading to a more stable configuration.
Types of Nuclear Decay:
Alpha Decay:
Process: Emission of an alpha particle (2 protons, 2 neutrons).
Change: Reduces the atomic number by 2, mass number by 4.
Example: Uranium-238 decays to thorium-234 by emitting an alpha particle.
Beta Decay:
Process: A neutron in the nucleus transforms into a proton, emitting a beta particle (electron or positron).
Change: Increases atomic number by 1; mass number remains unchanged.
Example: Carbon-14 decays to nitrogen-14 via beta decay.
Gamma Decay:
Process: Emission of gamma rays, which are high-energy photons, from an excited nucleus.
Change: The atom remains unchanged in atomic and mass number, but loses energy.
Half-Life:
The time required for half of a sample of a radioactive substance to decay.
Application: Used in radiometric dating, nuclear medicine, and understanding radioactive waste management
SEMESTER TWO SOPHOMORE PHYSICS:
1 Nuclear power
Nuclear energy
The energy stored in the nucleus of an atom
That energy hold the particles in the nucleus together
Nuclear fission
Nuclear fission is the process where the nucleus of an atom splits into smaller parts, releasing a large amount of energy.
It typically occurs in heavy nuclei like uranium-235 or plutonium-239 when they absorb a neutron.
Nuclear Fission:
Definition: Process where the nucleus of an atom splits into smaller parts, releasing a large amount of energy.
Applications: Used in nuclear power plants for electricity and atomic bombs for explosive energy.
Nuclear Fusion:
Definition: Process where two light atomic nuclei combine to form a heavier nucleus, releasing energy.
Occurs naturally in stars, including the sun, and is considered a potential future energy source due to its high energy output and low radioactive waste.
To produce nuclear fission:
Definition: The splitting of heavy nuclei (e.g., uranium-235, plutonium-239) after absorbing a neutron.
Key Outcome: Releases significant energy and additional neutrons, causing more fission.
Applications: Used in nuclear power plants and atomic bombs.
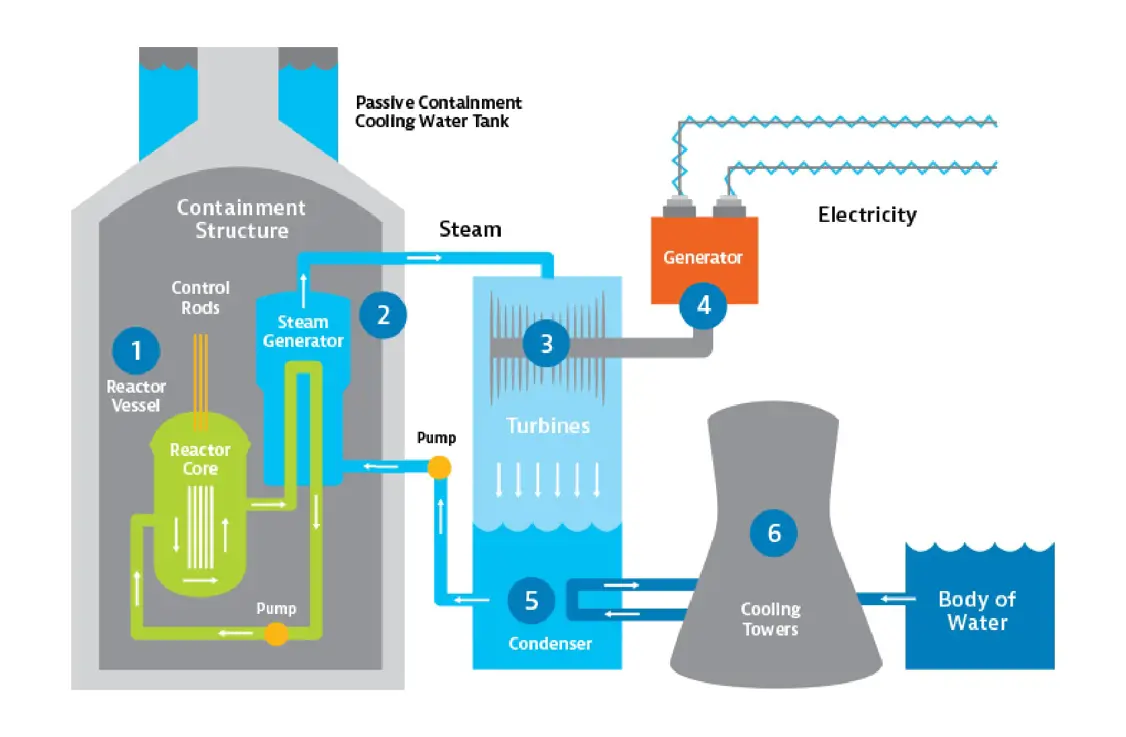
Generating electricity using nuclear energy -
Nuclear power plants generate electricity through the process of nuclear fission, where heavy atomic nuclei split apart, releasing heat that converts water into steam to drive turbines connected to generators, ultimately producing electrical energy.
Nuclear Fusion
Naturally Occurring: Fusion powers stars, including the sun, by converting hydrogen into helium.
High Energy Output: Produces more energy than fission with minimal radioactive waste.
Required Conditions: Needs extremely high temperatures and pressures to overcome nuclear repulsion.
Potential Applications: Ongoing research aims to harness fusion for sustainable electricity generation, contrasting with nuclear fission, which splits heavy nuclei to release energy and is used in current nuclear reactors and bombs.
Benefits of nuclear power
Nuclear power offers low greenhouse gas emissions, high energy density, reliable base-load energy supply, enhanced energy security, and long-term fuel availability.
Disadvantages of nuclear power
Disadvantages of nuclear power include the potential for catastrophic accidents, long-term radioactive waste disposal challenges, high initial construction costs, and concerns about nuclear proliferation.
2 Work, Energy, and Power
Equation for Work:
W = F ⋅ d
W: Work (in joules, J)
F: Force (in newtons, N)
d: Distance (in meters, m)
Work Definition:
Work occurs when you apply force over a distance and is measured in joules (J).
Cosine Factor:
W = F d cos(θ)
θ: Angle between the force vector and the direction of motion.
Kinetic Energy (KE):
Definition: Energy of an object in motion.
Formula: KE = 1/2 mv²
m: mass (kg)
v: velocity (m/s)
Work-Energy Principle:
The work done equals the change in kinetic energy.
Work (W):
Defined as the energy transfer when a force moves an object.
Formula: W = Fd cos(θ)
F: force (N)
d: displacement (m)
θ: angle between force and movement.
Potential Energy (PE):
Definition: Stored energy based on position.
Formula: PE = mgh
m: mass (kg)
g: gravity (9.81 m/s²)
h: height (m)
equations
Newton's Second Law: F = ma
Work: W = F ⋅ d
Kinetic Energy (KE): KE = 1/2 mv²
Potential Energy (PE): PE = mgh
Projectile Range: R = (v₀² * sin(2θ)) / g
Max Height: H = (v₀² * (sin²θ)) / (2g)
Quadratic Formula: x = (-b ± √(b² - 4ac)) / (2a)
Gravitational Force: F = G * (m₁ * m₂) / r²
PE spring: U = (1/2)kx², where U is the potential energy stored in the spring, k is the spring constant, and x is the displacement from the equilibrium position.
when qork is done oln a system energy chnages
to llose energy friction is used
ke=0
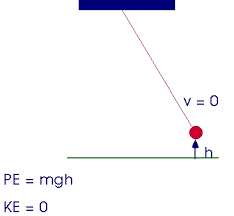
pe=0
ke1+pe1=ke2+pe2
watt= jules/second
3 Types of Energy
How is a heavy roller coaster able to keep going after it is initially hauled up a tall hill?
Energy is the ability to do work and move an object.
Energy is broken up into two general categories:
Potential Energy
Kinetic Energy
Joule
Energy is measured in joules, which is equivalent to kg*m²/s².
One joule is the amount of energy needed to apply a force of 1 newton over a distance of one meter.
An ordinary 100-watt electric light bulb uses over 100 joules of energy per second.
Potential Energy
Potential energy is stored in an object.
This type of energy can be a property of the object, such as the types of bonds in the molecules or the elasticity.
Gravitational Potential Energy
Potential energy due to an object's position above the Earth.
The higher an object is, the more gravitational potential energy (GPE) it has.
GPE depends on mass, height, and gravity.
Formula:
GPE = gravity (9.8 m/s²) × mass (kg) × height (m)
Elastic Potential Energy
Energy stored in an object when it is stretched or compressed.
Examples: Rubber bands, springs.
The object "springs" back to its original shape when released.
Chemical Potential Energy
Stored in the bonds of molecules.
Released during a chemical reaction.
Examples: Unlit match, batteries.
Nuclear Potential Energy
Stored in the nucleus of an atom.
Released when atoms split (nuclear fission) or fuse (nuclear fusion).
Example: Nuclear bombs before detonation contain this energy.
Kinetic Energy
Energy of motion.
Depends on mass and velocity.
Formula:
KE = ½ × mass × velocity²An increase in velocity has a greater effect on kinetic energy than an increase in mass.
Electrical Energy
Generated by moving charged particles (electrons).
Flows through metals in circuits.
Example: Electricity in homes.
Radiant Energy
Energy that travels in waves (electromagnetic radiation).
Example: Sunlight.
Includes radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, gamma rays.
Thermal Energy
Internal energy from vibrating molecules.
More heat = more molecular movement.
Heaters generate thermal energy.
Sound Energy
Energy from vibrating particles in a medium.
Travels as a mechanical wave.
Examples: Speakers, headphones.
Mechanical Energy
Combination of kinetic and potential energy.
Example: A roller coaster has high PE at the top and high KE when moving down.
Comparison: Potential Energy vs. Kinetic Energy
Potential Energy (PE)
Kinetic Energy (KE)
Stored energy
Energy of motion
Higher height = More PE
Higher speed = More KE
More PE = Less KE
More KE = Less PE
Conservation of Energy
Energy can change forms but cannot be created or destroyed.
Example: Bowling ball hits pins, transferring kinetic energy to them.
Law of Conservation of Energy: The total energy in a system remains the same.
4 Energy Efficiency
Learning Objectives:
Explain what is meant by energy efficiency.
Calculate the efficiency of energy transfers.
Examine the conservation of energy.
Keywords:
Conservation of energy
Efficiency of energy.
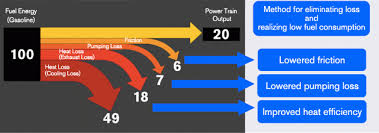
Whenever there is a change in a system, energy is transferred and some of that energy is dissipated.
Dissipation refers to the loss of energy, often in the form of heat, due to friction or other non-conservative forces.
This loss affects the overall efficiency of the system.
It highlights the importance of minimizing energy waste in practical applications.
Traditional filament bulbs are being replaced by more efficient fluorescent or LED bulbs.
Fluorescent and LED bulbs are 60% and 70% more efficient than filament bulbs.
List five impacts that this will have:
Energy Savings: Reduced energy consumption will lead to lower electricity bills for consumers and businesses.
Decreased Carbon Footprint: With less energy used, there will be a corresponding reduction in greenhouse gas emissions associated with electricity generation.
Longer Lifespan: LED and fluorescent bulbs typically last much longer than traditional filament bulbs, resulting in less frequent replacements and reduced waste.
Improved Lighting Quality: These new lighting technologies often provide better light quality and color rendering, enhancing visibility and aesthetics in various settings.
Economic Growth: Increased demand for energy-efficient lighting can stimulate job creation in manufacturing, distribution, and installation sectors.
Calculation of energy efficiency:
Efficiency is an indication of how much energy supplied to a device is transferred as a useful output.
If all of the energy supply was transferred usefully, the transfer would be 100% efficient
Efficiency Example Notes

Efficiency = (Useful energy output / Total energy input) × 100
Example:
Work done: 7500 J
Energy used: 44,000 J
Efficiency = 17% (most energy is lost as heat or friction).
Conservation of Energy Principle
Energy can be transferred usefully, stored, or dissipated but can never be created or destroyed.
Total energy input: 44,000 J
Useful energy output: 44,000 J x 0.17 = 7,480 J
Energy lost: 44,000 J - 7,480 J = 36,520 J (primarily as heat and friction).
The conservation of energy means that there is no net change to the total energy in a closed system; therefore, the energy input must equal the sum of useful energy output and energy lost.
Energy cannot be created or destroyed, only transferred from one store to another in a closed system. The total energy put into a system must equal the sum of the useful energy output and the energy lost.
We say that energy is conserved. This law of conservation of energy states that while energy is conserved, only some of the energy output is useful to us; the rest is dissipated as waste energy. This affects the efficiency of a machine.
explain why heating a material does not just oncrease the thermal energy stored of the material
null some of the energyu goes is abored as the netal expands this means that the energu goes into the metals elastic energy stores
5 Volume vs. Area
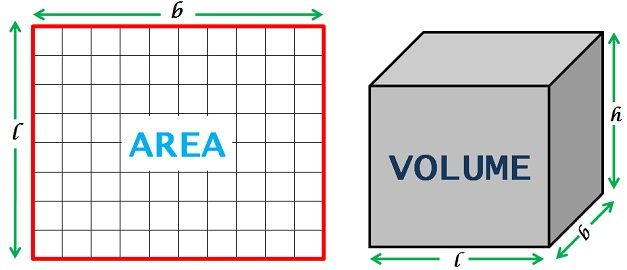
Area
Refers to 2-dimensional measurements of space inside an object.
Formula: length × width
Volume
Refers to 3-dimensional measurements of space inside an object.
Formula: length × width × height
Net
A pattern of shapes that, when cut out and folded, will become a 3D object.
Finding the Volume of Your Container
Use the cubes you created and the plastic cubes provided to fill your container.
Then, count the number of cubes you used to fill the container.
Weight in Volume
A gram is defined as the mass of one cubic centimeter of water.
A liter is defined as the unit of volume within the metric system, equating to one cubic decimeter.
Volume
refers to 3-dimensional measurements of space inside an object
lengthxwidthxheight
net: a pattern of shapes when cut out and folded will becoem a 3d object
Finding the volume of your contianer
use the cubes you ceated. and the plastic cubes provided to gill your containter
then count the number of cudes you used to fill the container
weight in volue
gram is defines as the mass of one cubic centimeter of water
liter is defined as the u it of volume within the metric system equating on cubic decimeter
6 Thermodynamics
TemperatureA measurement that describes the average kinetic energy in random thermal motion per atom or molecule.
Thermometers - A calibration tool to measure temperature changes.
Three Different Scales
Fahrenheit
Celsius
Kelvin: The base unit of temperature in the International System of Units, having the unit symbol K.
Thermal Energy - Thermal energy is produced when a rise in temperature causes atoms and molecules to move faster and collide with each other.
Internal Energy - The energy associated with the random, disordered motion of molecules within the system.
Entropy - The degree of disorder or randomness in the system.
Entropy and States of Matter - The more disordered the molecules are, the higher the state of entropy; entropy increases as temperature increases.

Absolute Zero - All kinetic energy stops. The minimum possible temperature is 0 K, or -273 °C (-459 °F).
Heat - Changes both the temperature and the state of matter. Heat travels from high to low temperatures.
Laws of Thermodynamics
Zero Law - Temperature: Thermal equilibrium is transitive
First Law - Conservation of Energy: energy cannot be created or destroyed, only changed into another form.
Second Law - Heat: Heat always flows from hot to cold.
Third Law - Entropy: As temperature approaches absolute zero, entropy is at a constant minimum.
Heat transfer Meathod
conductuin the transfer of heat through or between materials by direct contact
convectuuon the transfer of heat by the motion of liquids and gases
thermal co ductorfer
materials that transfer heat redily
thermal isulatiors materials that dont transfer heat
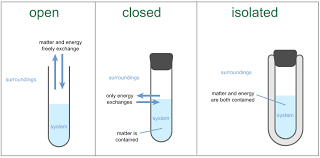
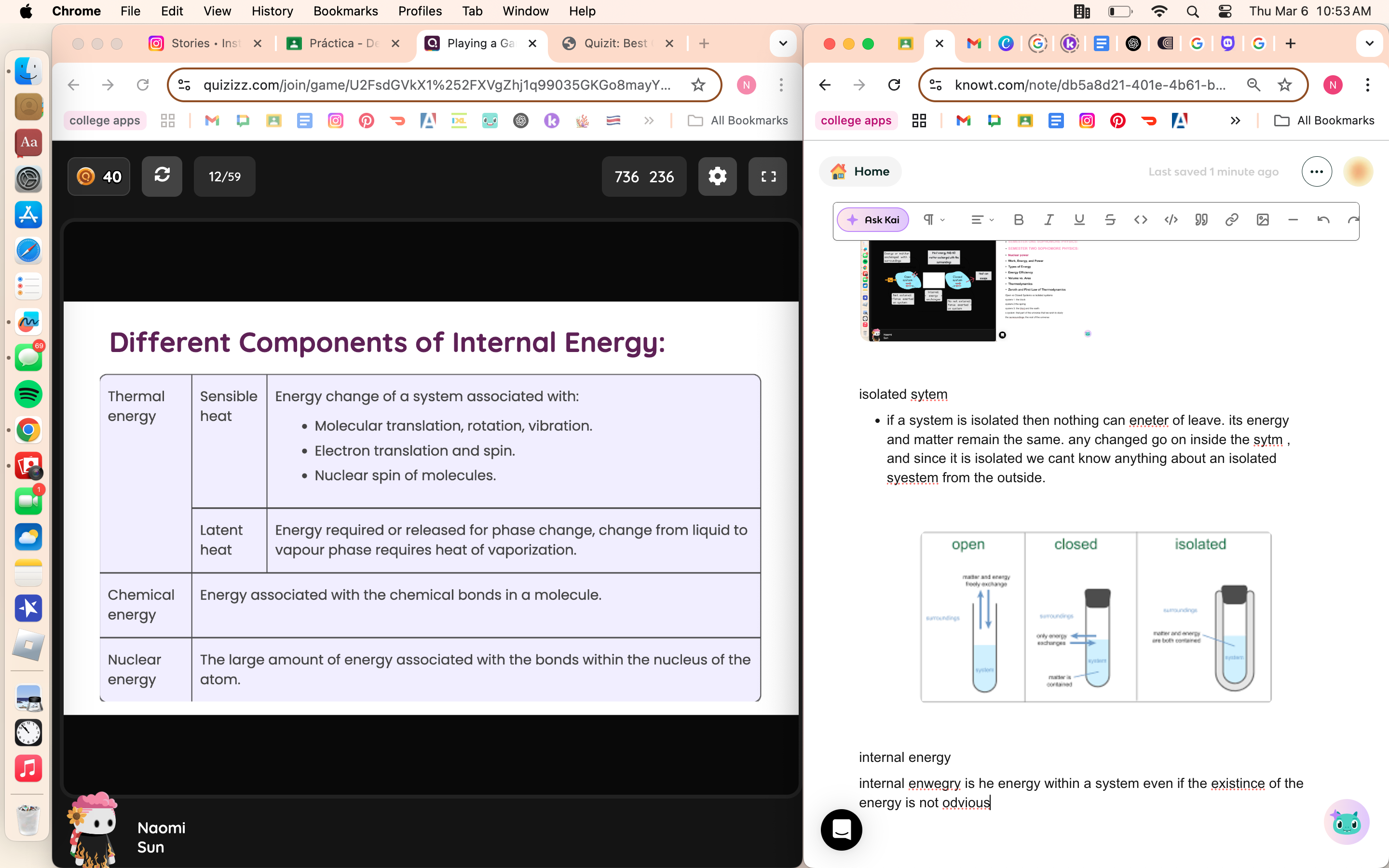
7 Open, Closed, and Isolated
Open vs Closed Systems vs isolated systems
system 1: the block
system 2 the spring
system 3: the blocj and the earth
s system: that part of the universe that we wish to study
the surreoundings: the rest of the universe
isolated sytem
if a system is isolated then nothing can eneter of leave. its energy and matter remain the same. any changed go on inside the sytm , and since it is isolated we cant know anything about an isolated syestem from the outside.
internal energy
internal enwegry is he energy within a system even if the existince of the energy is not odvious
first law of thermodynacims
delta u=q+w
delat u is the chanfge in internak=al energy kf the susentm q is added and w is the work added
q is positive when added and negative if take oyt




isochoric (V=cte)
applying the first law of thermo dynamics>
delta U= Q - W
if deltaV=0
we get:
delate U=Q


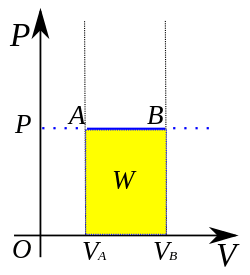
isobaric Process(P=cte)
as you can notice, W=P delta V is =- to the area below the graph
Isothermic (T=Cte
scince internal energy gas depends exclusivly on its temp. the total change in internal energy is delta U and its 0
delta u=Q-W

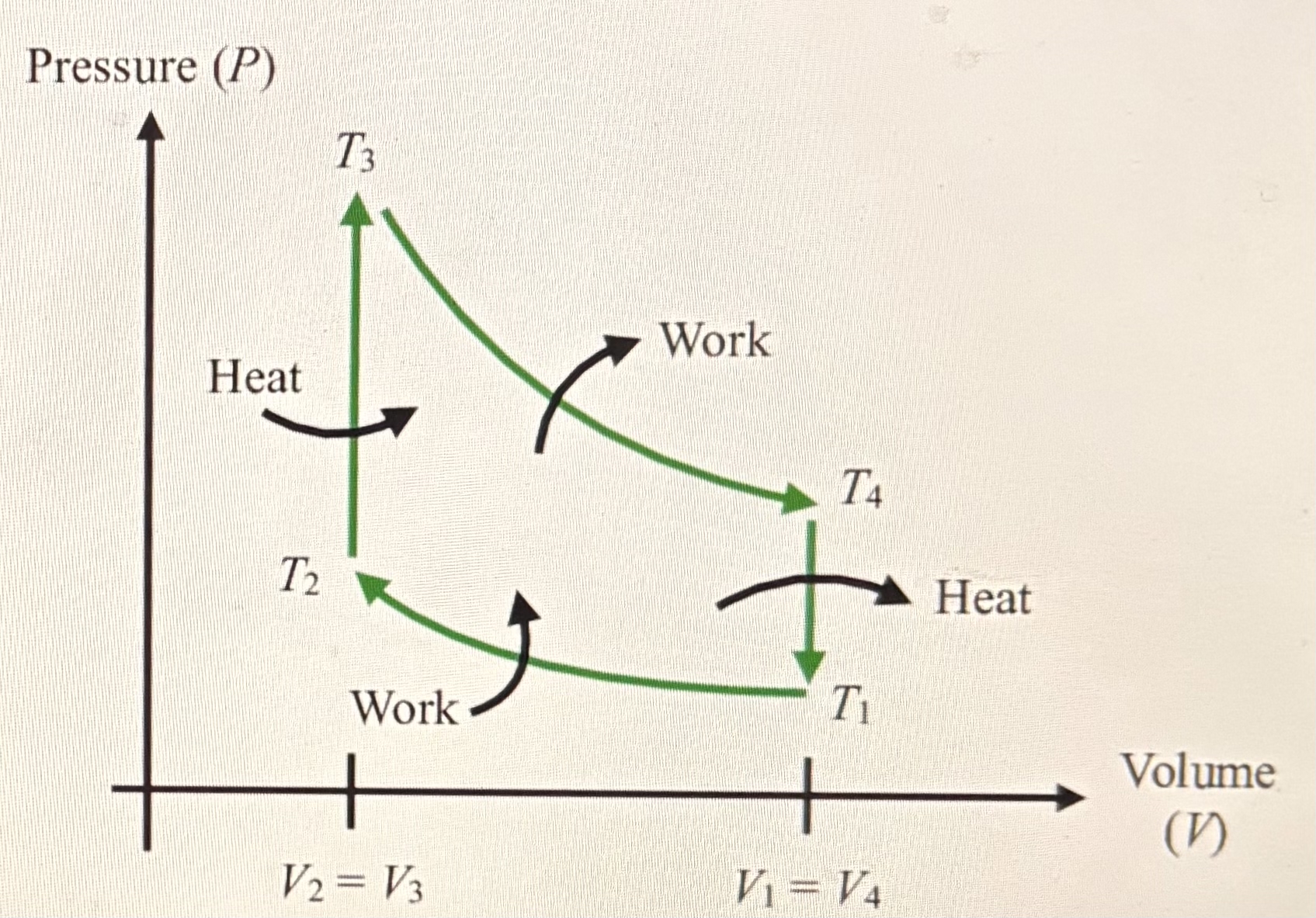
Thermodynamic cycle
A thermodynamic cycle consists of a linked sequence of thermodynamic processes that involve transfer of heat and work into and out of the system, while varying pressure, temperature, and other state variables within the system, and that eventually returns the system to its initial state.
8 ideal gas law
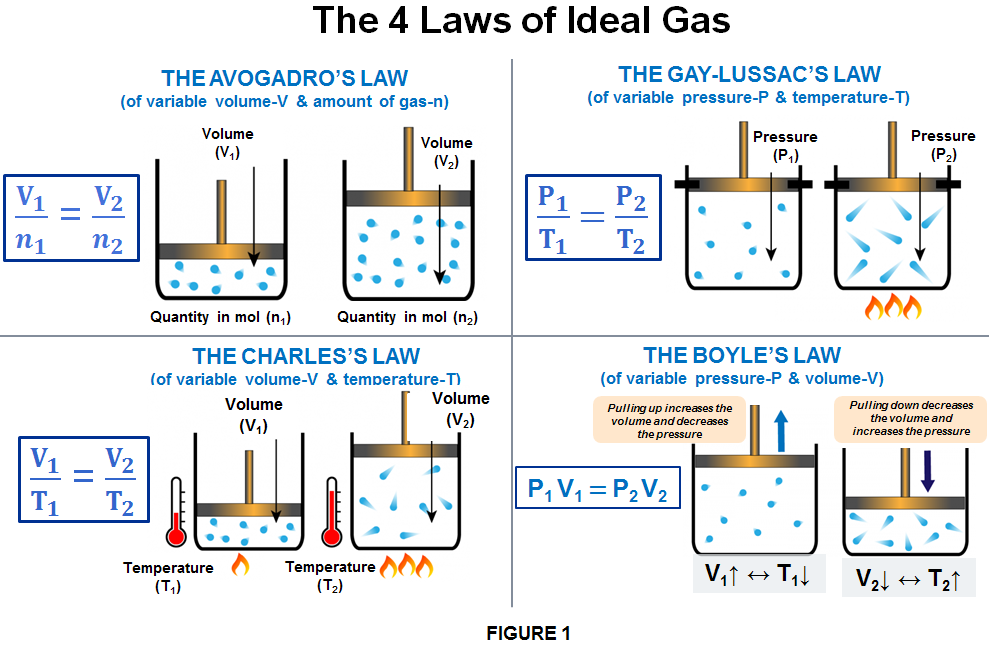
The ideal gas law relates the macroscopic properties of gases to one another.
Volume - amount of space occupied by gas.
Temperature - measurement of the average kinetic energy of the gas molecules.
Amount - measured in moles.
Pressure - force exerted on the surface by molecular collisions.
Volume and Pressure:
As volume decreases, pressure increases; less surface area results in a greater number of collisions. Pressure and volume are inversely proportional.
Temperature and Pressure:
As the average kinetic energy of the molecules increases, pressure also increases as collisions occur more frequently and with greater energy. Pressure is directly proportional to absolute temperature (Kelvin).
Moles and Pressure:
Ideal Gas Law: PV = nRT
Where:
P = pressure (atm)
V = volume (L)
n = number of moles
R = 0.0821 L·atm/mol·K
T = temperature (K)
Conversions:
1 atm = 760 mmHg = 760 torr
°C + 273 = K
1 mole = 6.022 × 10²³ particles (Avogadro’s number)
Ideal Gas Law Assumptions:
Particles are so small they have no volume.
No attractions or repulsions between them.
Particles are in constant, random motion.
All collisions are elastic (no energy loss).
Average kinetic energy is directly proportional to temperature (K).
Gas Pressure: Comes from collisions of gas particles with container walls. More collisions = higher pressure.
Absolute Temperature (Kelvin): Needed because it's directly proportional to kinetic energy. 0 K = no motion.
Molar Volume at STP: At standard temperature and pressure (0°C, 1 atm), 1 mole of gas occupies 22.4 L.
Real vs Ideal Gases: Real gases deviate under high pressure and low temperature due to interactions and volume.
Kinetic Molecular Theory: Gas behavior explained by particle motion — faster particles = more energy.
Practice Problem Solutions
Practice Problem One:
A sample of oxygen gas has a volume of 3.52 L at 27ºC and 800.0 torr. How many oxygen molecules does it contain?
T = 27 + 273 = 300 K
P = 800.0 torr ÷ 760 = 1.053 atm
n = PV / RT = (1.053)(3.52) / (0.0821)(300) ≈ 0.150 moles
Molecules = 0.150 mol × 6.022×10²³ ≈ 9.03 × 10²² molecules
Practice Problem Two:
If 2.0 moles of gas in a sealed glass flask is heated from 25ºC to 50ºC, what can be said about kinetic energy, pressure, and the number of moles?
Kinetic Energy ↑
Pressure ↑ (Volume is constant)
Moles = constant (sealed system)
Practice Problem Three:
A mixture of gases contains 1.5 moles of oxygen, 3.0 moles of nitrogen, and 0.5 moles of water vapor. If the total pressure is 700 mmHg, what is the partial pressure of the nitrogen gas?
Total moles = 1.5 + 3.0 + 0.5 = 5.0 moles
Mole fraction of N₂ = 3.0 / 5.0 = 0.6
Partial pressure = 0.6 × 700 mmHg = 420 mmHg
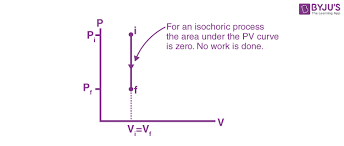
9 Understand isochoric processes and thermodynamics
Volume stays the same
No work is done
Formula:
W = PΔV = 0
All heat added goes into internal energy:
Q = ΔU
First Law of Thermodynamics
Formula:
ΔU = Q - WIn isochoric:
ΔU = Q
PV Graph for Isochoric
Vertical line (volume doesn’t change)
What happens when heat is added?
Temperature goes up
Pressure goes up (if volume is fixed)
Internal energy increases
Internal Energy Formula
ΔU = nCvΔT
n= molesCv= heat capacity at constant volumeΔT= temp change
Heat Capacities
Diatomic gas:
Cv = 5/2 RCp = Cv + R = 7/2 R
Diatomic Gases
Oxygen (O₂), Nitrogen (N₂), etc.
Trick: Have No Fear Of Ice Cold Beer
Key Quiz Facts
Isochoric = no work
Pressure ∝ Temperature
Oxygen is diatomic
PV graph = vertical line
Heat added → temp & pressure go up
ΔU = Q if volume is constant
10 Architectural Styles
Brutalism: Characterized by massive forms and rough concrete finishes, focusing on functionality.

Bauhaus: Combines crafts and fine arts; known for simplicity and minimalism.
Gothic: Noted for pointed arches and verticality; features elaborate ornamentation.
Islamic: Features intricate geometric patterns and often includes domes and minarets.
Art Deco:
Characteristics: Vibrant colors, geometric shapes, luxury materials.
Examples: Chrysler Building, Miami Beach hotels.
Baroque:
Characteristics: Ornate details, grandeur, dramatic light use.
Examples: St. Peter's Basilica, Versailles Palace.
Classical:
Characteristics: Symmetrical proportions, columns, harmony.
Examples: Parthenon, Pantheon.
Modernist:
Characteristics: Minimalist, functional, rejection of ornamentation.
Examples: Villa Savoye, Seagram Building.
Bauhaus: Combines crafts and fine arts, known for simplicity and minimalism.
Gothic: Noted for pointed arches and verticality, features elaborate ornamentation.
Islamic: Features intricate geometric patterns and often includes domes and minarets.
Art Deco
Characteristics: Vibrant colors, geometric shapes, luxury materials.
Examples: Chrysler Building, Miami Beach hotels.
Baroque
Characteristics: Ornate details, grandeur, dramatic light use.
Examples: St. Peter's Basilica, Versailles Palace.
Classical
Characteristics: Symmetrical proportions, columns, harmony.
Examples: Parthenon, Pantheon.
Modernist
Characteristics: Minimalist, functional, rejection of ornamentation.
Examples: Villa Savoye, Seagram Building.
11 wave mechanics
A wave is a disturbance through a medium that carries energy from one place to another.
Types of Waves: a wave is a disturbance thru a medium that carries energy from one placew to another
mechanical
requires a medium
ex sound or ripples in a pornd, sptings
elector magnetic
canm travel in empty space
ex uv rays, radio waves, gamma rays
transverse waves
cause the particles of the medium to move pedrpendicular to the dikrection the wave is traveling
longitudinal waves
causes the particles of the medium to movbe parallel to the directionm the wave is traveling
frequency - (f)
the number of waves per second
1 cycle per secpond = 1 hertz (HZ)
does not change from one medium to the other
period (T) -measured in seconds
the number of seconds per wave
T=1/f
amplitude - (A)
the maxium displacement of particles in a medium from the point of equallibrium
wavelenth - meters
the distance between a ny two consecutibve points
speed (v) - (m/s)
the speed oof wave depends on the properties of the medium it is traveling thru
electromagnetic spectrum
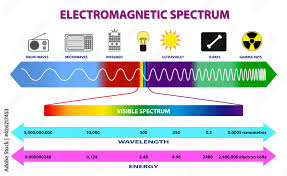
principle of superposition
when teo waves are traveling independently thru the same medium, the resultant displacement of any particle at a given time is the vector sum of the displacements that the individual waves acting alone would give it
when two wave puleses
constructive interference
two waves combimne to make a resultant a bigger wave
deconstuctive
two waves combine to make a resultant smaller wave
12 Hookes laws
the force extered on a spri resultes in a stretch or compression of the spring
in physics, some textbooks fefer to the F spring on object as the restoring force since the spring is trying to pull itself back into equallibrim (its unstretched position)
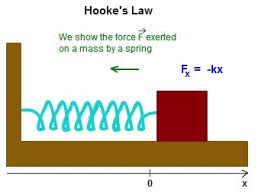
the force is constand to both springs…
f=(4cm)k
f=(∆x)(1/2k)
so (4cm)k= (∆x)(1/2k)
k cnacels, thus 4/(1/2)∆x
so the new strech is 8cm
elastic potential enegry
Us =1/2kx²
where Us =elastic potential energy
k=spring constant
x= spring stretch(or compression
an oscillation is a back anf fourth motion of an b=object between 2 points
Simple Harmonic Motion
Oscillatory motion is a repetitive back and forth movement about an equilibrium position within a fixed amount of time. Important terms related to oscillatory motion include:
Period: The time taken to complete a full cycle. The unit for period is seconds. In the previous animations, the period was four seconds.
Frequency: The number of cycles per second. The unit for frequency is hertz (Hz), which is equivalent to 1/s. In the previous animations, the frequency was 2.5 Hz, indicating it traveled a quarter of the way in one second.
`Graphing Oscillatory Motion: If you plot a position v time graph of an oscillating object and it creates a sinusoidal graph (sine or cosine func), the oscillation is described as simple harmonic motion (SMH).


What is Simple Harmonic Motion:
- Simple Harmonic motion is a simple type of oscillation where the net force can be described by Hooke’s law:the resting force is directly proportional to the displacement
the restoring force is in the opposite direction of the displacement
- We will focus of SHM for springs and pendulums
SHM of Springs
A spring attached to block m is stretched with displacement x, and when released, the spring force brings the block back towards the equilibrium position.
The block passes the equilibrium position because of the momentum and then compresses the spring with a displacement of x. The spring force brings it back towards the equilibrium position.
Spring Amplitude
The amount the spring is displaced from the equilibrium as it stretches the amplitude
This is the same displacement form the equilibrium
Energy of the Oscillating Spring
At the max compression and the extension, the mass comes to a temporary stop, causing the KE to be zero and all the every stored as Us
At the equilibrium position (x=0), the mass at its greatest speed and all the energy is KE
Period of a Spring
Ts - Period of a spring (s)
m - Mass (Kg)
k- Spring constant (N/m)
Position during SHM
To time out the position of an object at given time as it undergoes simple harmonic motion
x(t)=A cos (2πft)
x- Position at time t
A- Amplitude
f - frequency
t- time
What is a Pendulum
An object that hyas a small mass, knows as a pendulum bob, hunger from a pivot point by a light wire or string
Restoring Force of a Pendulum
Wgat is the resporing force of a pendulum
weight!
When you lift a pendulum bob up a certian angle the gh=hoizontal compnent of the weight (mg sin 0) is the resporing force
Energy of a Pendulum
Ug=)j(at equalibriu,m)
KE= ½ mv3 (max v)
HR classifications
classifications of celestial bodies
Celestial bodies are objects found in space, and they fall into several main types. Stars are massive, glowing spheres of gas that produce light and heat through nuclear fusion. Planets orbit stars, are spherical, and have cleared their orbits of other debris. Dwarf planets also orbit stars and are spherical but haven’t cleared their orbits. Moons are natural satellites that orbit planets. Other classifications include asteroids, which are rocky bodies, and comets, which are icy bodies that release gas and dust when near the Sun.
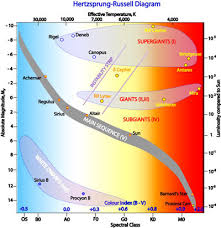
Vocabulary words:
spectral class: determines the color of a star
luminocity measures the brightness of a star
HR diagram: used to classidy stars by their tempature