Game Theory and Strategic Thinking - chapter 9

9.1. Games and Strategic Behaviour

• Game: a situation involving at least two people that requires those involved to think strategically
• Game theory: the study of how people behave strategically under different circumstances
• behaving strategically: acting to achieve a goal by anticipating the interplay between your own and others’ decisions
• Games have rules, which define the actions players are allowed to take
• Strategies: are plans of action that players can follow to achieve a desired goal
• Payoffs: the rewards that come from taking particular actions

9.2. One-Time Games and the Prisoners’ Dilemma

• Prisoners’ dilemma: a game of strategy in which two people make rational choices that lead to a less-than-ideal result for both
• 
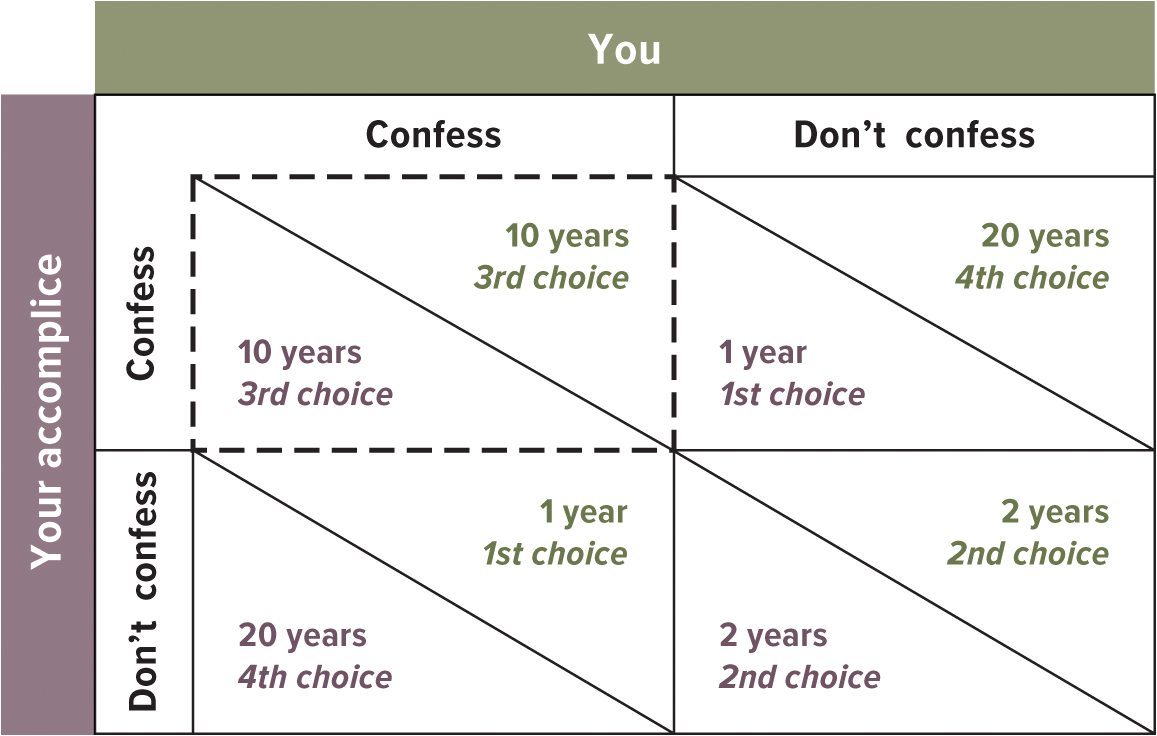
• Each player has a choice to cooperate or not to cooperate
• Each prefers mutual cooperation to mutual non-cooperation
  • But non-cooperation is the best choice because its payoff is higher no matter what strategy other players choose
• In this game, pursuing you own self-interest leaves everyone worse off

9.3. Finding the Dominant Strategy

• Dominant strategy: When a strategy is the best one to follow no matter what strategy other players choose
• 
• Not all games feature a dominant strategy
  • In some games there is no single strategy that will work best for you

9.4. Reaching Equilibrium

• When all players choose the best strategy they can, given the choices of all other players, those players have reached a Nash equilibrium
• Players who have reached a Nash equilibrium have no reason to regret their decision
  • This doesn’t necessarily mean that an equilibrium outcome to a game is a good one
  • We can see both negative-negative and positive-positive outcomes in equilibrium
  • The only condition is that there’s no incentive to switch from one decision to another

9.5. Avoiding Competition Through Commitment

• In the prisoners’ dilemma, the players of the game would be better off if they could cooperate and make a deal beforehand not to confess
• 
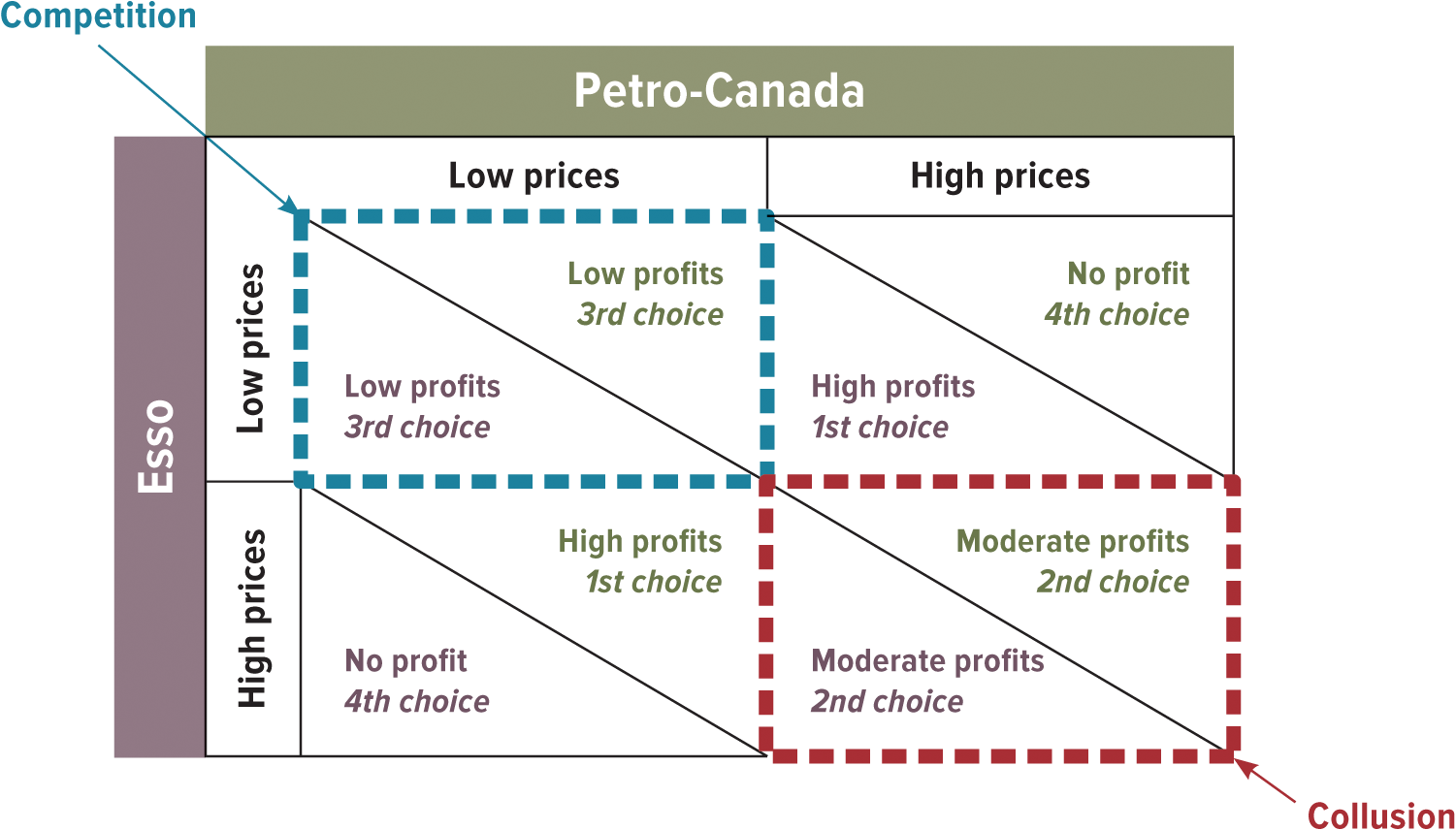
• However, even if you know you accomplices will not confess, you are still better off confessing
• To solve the problem, players may sometimes reach a mutually beneficial equilibrium by pursuing a commitment strategy
  • Where they agree to submit to a penalty if they defect from the equilibrium

9.6. Repeated Play in the Prisoners’ Dilemma

• In a repeated game, players can penalize each other for defecting in one round by punishing each other in the next round
• As a result, the players can sometimes achieve a mutually beneficial equilibrium, even when they couldn’t do so in a single game
• A common strategy in repeated games is tit-for-tat, in which a player takes the same action as their opponent in the previous round
• Anyone who is playing against a person with a tit-for-tat strategy has a strong incentive to cooperate because defecting would push them into a less profitable equilibrium in every future round of the game

9.7. Think Forward, Work Backward

• Backward induction is the process of analyzing a problem in reverse
  • Starting with the last choice, then the second to last choice, etc
• This problem-solving tool can be used to choose between options with different consequences down the road
  • You first choose the goal you are trying to reach and then determine the steps needed to reach it

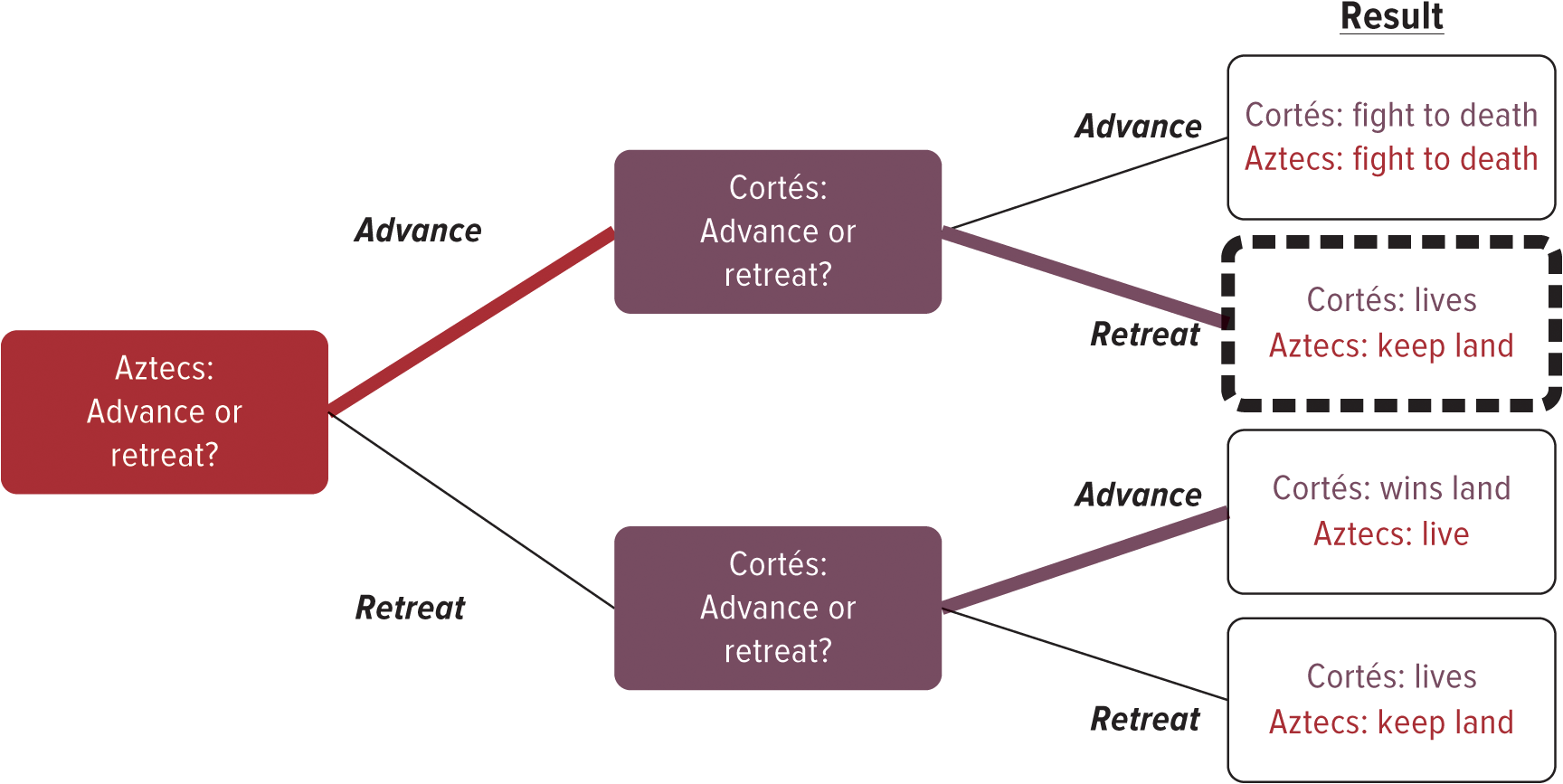
9.8. Deterring Market Entry: A Sequential Game

• In many situations, one person or company must make a decision before the other one
  • These situations can be represented as games in which players move sequentially rather than simultaneously
  • Because the payoff each achieves still depends on the other’s decision, the player who moves first must anticipate the decision the next player will make in response
• Decisions can be diagrammed as the nodes in a decision tree, which branch off into the choices or payoffs that follow from each option
• 
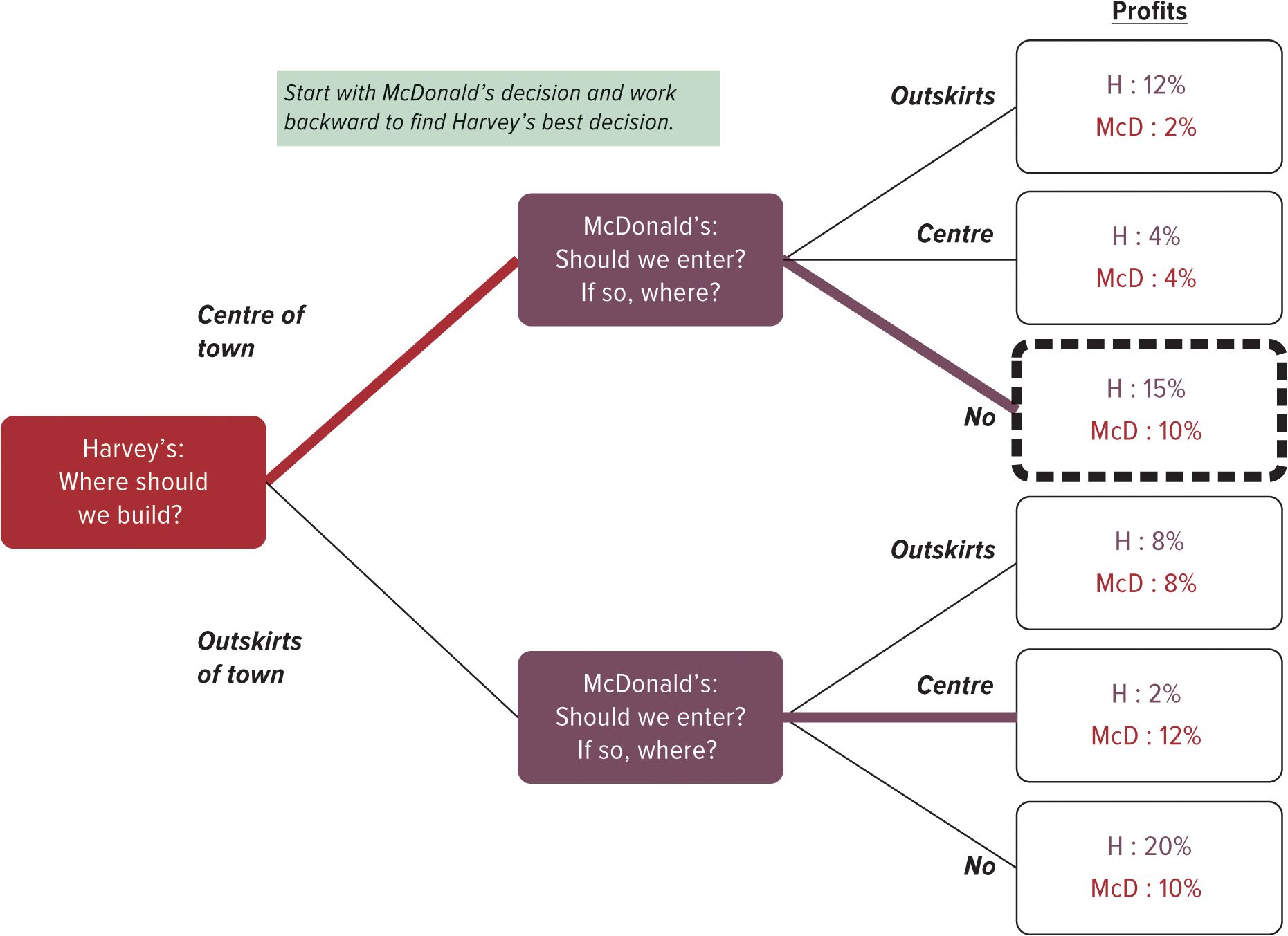
• Backward induction can be used to analyze decision tree and determine the best course of action at each stage of the game

9.9. First-mover Advantage in Sequential Games

• In a game with first-mover advantage, the player who moves first gets a higher payoff than those who follow
• Example: a one-round bargaining game in which the person who makes the first offer gets virtually everything
• The ability to bargain over multiple rounds of offers and counter-offers dilutes the first-mover advantage
• 

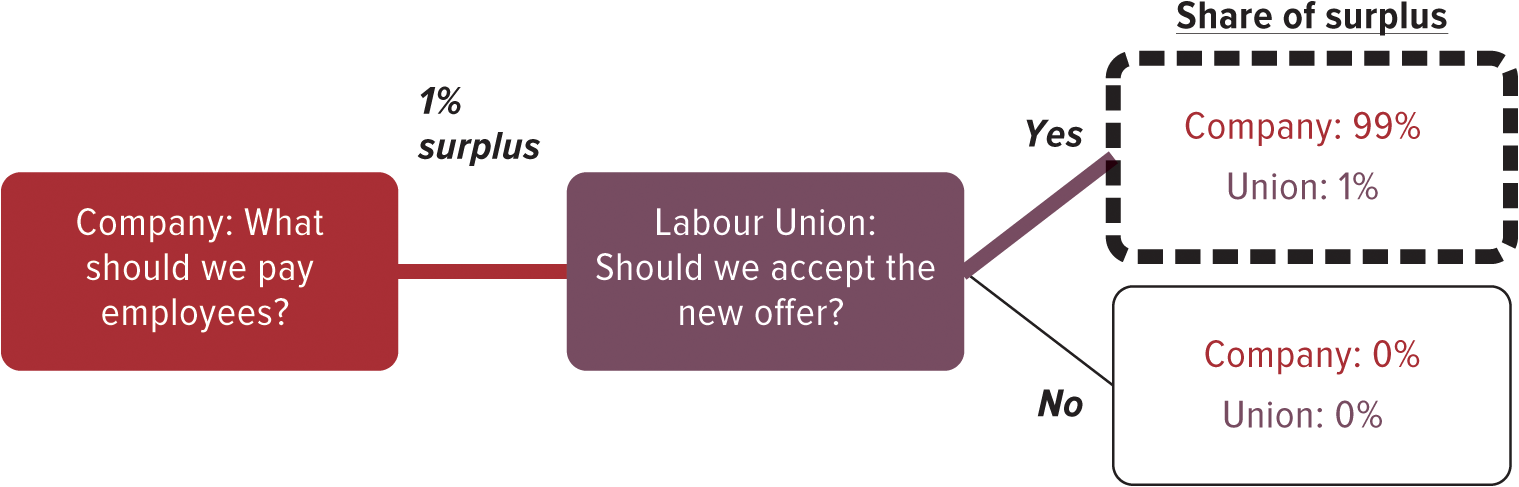
9.10. Repeated Sequential Games

• The ability to make counter-offers transforms bargaining from a game in which first-mover advantage trumps everything into a game of patience
• Bargaining takes time
  • In every round of bargaining that takes place before the players reach agreement, the value of the payoff they are splitting goes down
• The more patient player who places more value on money in the future relative to money in the present, has an advantage
• The surplus will be divided in proportion to the patience of each player

9.11. Commitment in Sequential Games

• In a sequential game, limiting your own choices can change your opponent’s behaviour

• Example: following a commitment strategy turns a non-credible threat into a credible one, changing the payoffs associated with an opponent’s options