Multilayer Perceptrons
A multilayer perceptron is a type of feedforward neural network consisting of fully connected neurons with a nonlinear kind of activation function. It is widely used to distinguish data that is not linearly separable.
MLPs have been widely used in various fields, including image recognition, natural language processing, and speech recognition, among others. Their flexibility in architecture and ability to approximate any function under certain conditions make them a fundamental building block in deep learning and neural network research. Let's take a deeper dive into some of its key concepts.
Input layer
The input layer consists of nodes or neurons that receive the initial input data. Each neuron represents a feature or dimension of the input data. The number of neurons in the input layer is determined by the dimensionality of the input data.
Hidden layer
Between the input and output layers, there can be one or more layers of neurons. Each neuron in a hidden layer receives inputs from all neurons in the previous layer (either the input layer or another hidden layer) and produces an output that is passed to the next layer. The number of hidden layers and the number of neurons in each hidden layer are hyperparameters that need to be determined during the model design phase.
Output layer
This layer consists of neurons that produce the final output of the network. The number of neurons in the output layer depends on the nature of the task. In binary classification, there may be either one or two neurons depending on the activation function and representing the probability of belonging to one class; while in multi-class classification tasks, there can be multiple neurons in the output layer.
Weights
Neurons in adjacent layers are fully connected to each other. Each connection has an associated weight, which determines the strength of the connection. These weights are learned during the training process.
Bias neurons
In addition to the input and hidden neurons, each layer (except the input layer) usually includes a bias neuron that provides a constant input to the neurons in the next layer. Bias neurons have their own weight associated with each connection, which is also learned during training.
The bias neuron effectively shifts the activation function of the neurons in the subsequent layer, allowing the network to learn an offset or bias in the decision boundary. By adjusting the weights connected to the bias neuron, the MLP can learn to control the threshold for activation and better fit the training data.
Note: It is important to note that in the context of MLPs, bias can refer to two related but distinct concepts: bias as a general term in machine learning and the bias neuron (defined above). In general machine learning, bias refers to the error introduced by approximating a real-world problem with a simplified model. Bias measures how well the model can capture the underlying patterns in the data. A high bias indicates that the model is too simplistic and may underfit the data, while a low bias suggests that the model is capturing the underlying patterns well.
Activation function
Typically, each neuron in the hidden layers and the output layer applies an activation function to its weighted sum of inputs. Common activation functions include sigmoid, tanh, ReLU (Rectified Linear Unit), and softmax. These functions introduce nonlinearity into the network, allowing it to learn complex patterns in the data.
Training with backpropagation
MLPs are trained using the backpropagation algorithm, which computes gradients of a loss function with respect to the model's parameters and updates the parameters iteratively to minimize the loss.
Workings of a Multilayer Perceptron: Layer by Layer
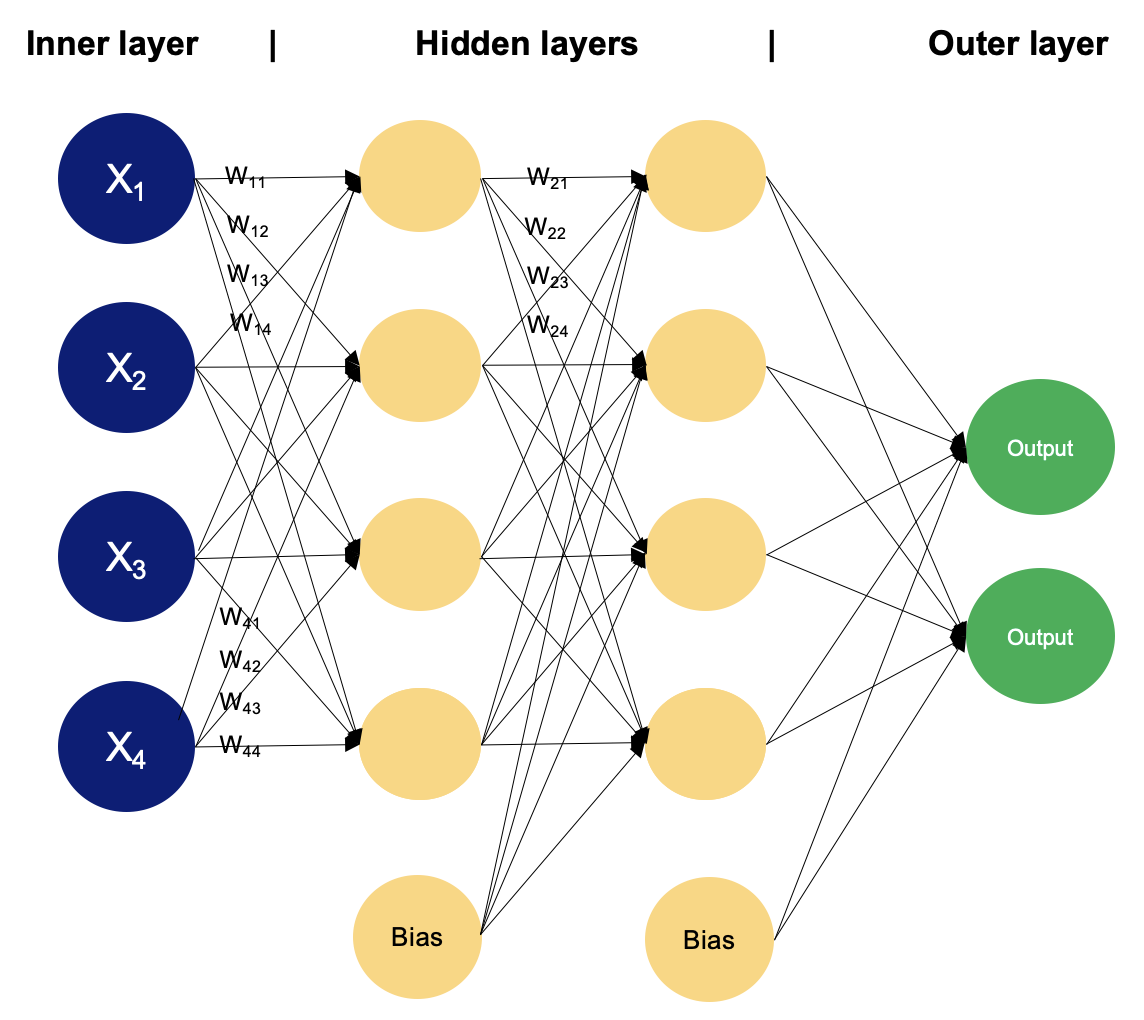
Example of an MLP with two hidden layers. Image by Author
In a multilayer perceptron, neurons process information in a step-by-step manner, performing computations that involve weighted sums and nonlinear transformations. Let's walk layer by layer to see the magic that goes within.
Input layer
The input layer of an MLP receives input data, which could be features extracted from the input samples in a dataset. Each neuron in the input layer represents one feature.
Neurons in the input layer do not perform any computations; they simply pass the input values to the neurons in the first hidden layer.
Hidden layers
The hidden layers of an MLP consist of interconnected neurons that perform computations on the input data.
Each neuron in a hidden layer receives input from all neurons in the previous layer. The inputs are multiplied by corresponding weights, denoted as
w. The weights determine how much influence the input from one neuron has on the output of another.
In addition to weights, each neuron in the hidden layer has an associated bias, denoted as
b. The bias provides an additional input to the neuron, allowing it to adjust its output threshold. Like weights, biases are learned during training.For each neuron in a hidden layer or the output layer, the weighted sum of its inputs is computed. This involves multiplying each input by its corresponding weight, summing up these products, and adding the bias:
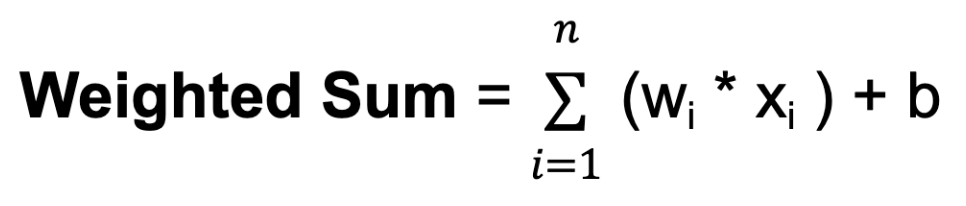
Where n is the total number of input connections, wi is the weight for the i-th input, and xi is the i-th input value.
The weighted sum is then passed through an activation function, denoted as
f. The activation function introduces nonlinearity into the network, allowing it to learn and represent complex relationships in the data. The activation function determines the output range of the neuron and its behavior in response to different input values. The choice of activation function depends on the nature of the task and the desired properties of the network.
Output layer
The output layer of an MLP produces the final predictions or outputs of the network. The number of neurons in the output layer depends on the task being performed (e.g., binary classification, multi-class classification, regression).
Each neuron in the output layer receives input from the neurons in the last hidden layer and applies an activation function. This activation function is usually different from those used in the hidden layers and produces the final output value or prediction.
During the training process, the network learns to adjust the weights associated with each neuron's inputs to minimize the discrepancy between the predicted outputs and the true target values in the training data. By adjusting the weights and learning the appropriate activation functions, the network learns to approximate complex patterns and relationships in the data, enabling it to make accurate predictions on new, unseen samples.