Chapter 1: Mathematics Review
1.1 Introduction
Some basic mathematical skills which need to be adequately mastered to enjoy the beauty of physics.
1.1 Exponents
Exponents are frequently used in physics.
3⁴=3×3×3×3=81
The superscript 4 is referred to as an exponent. The base number 3 is said to be raised to the fourth power.
Algebraic symbols can also be raised to a power —for example x⁴.
Where the exponent is 1, it’s typically not written x¹=x.
There are special names for when the exponent is 2 or 3.
When the exponent is 2, we say the quantity is squared.
Example x² means x is squared.
When the exponent is 3, we say the quantity is cubed.
Example x³ means x is cubed.
Negative exponents are used for reciprocals:

Exponents can also be fractions.
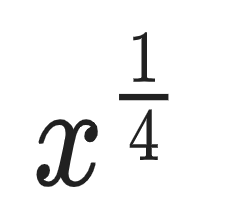
Rules of exponents
The product rule:
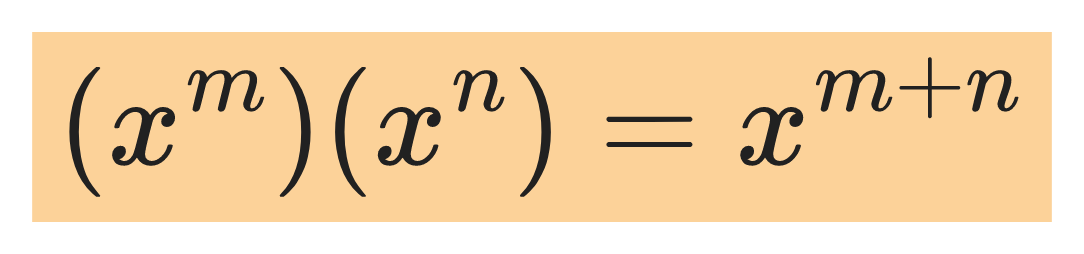
For example:
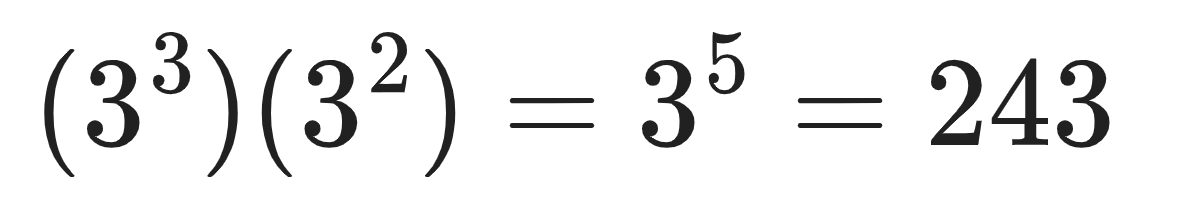
The quotient rule:
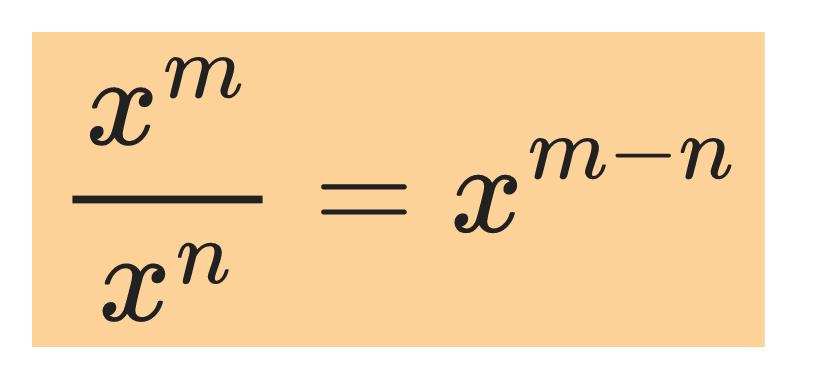
For example:
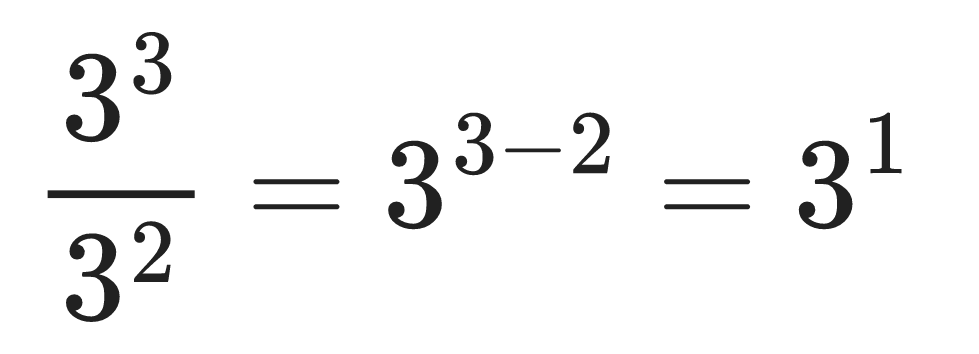
Special case of the quotient rule:
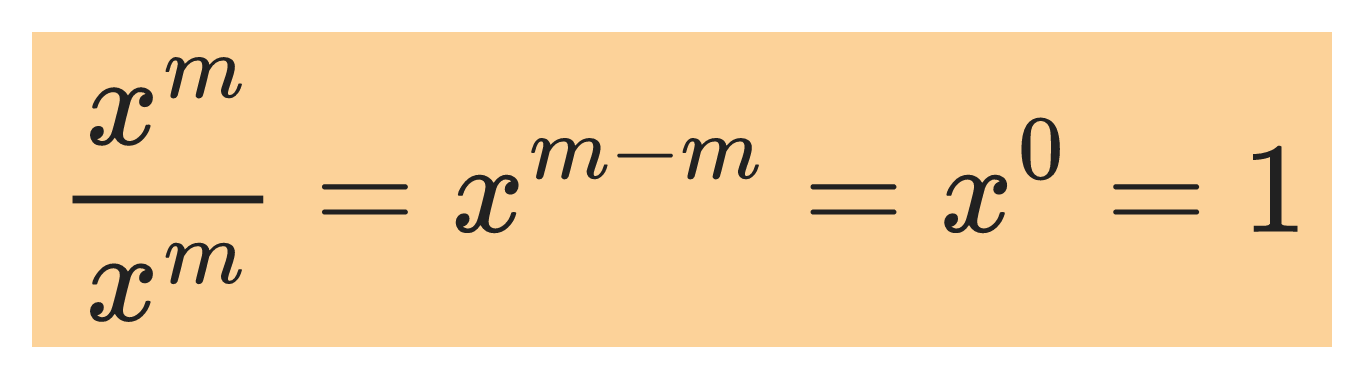
The first power rule:
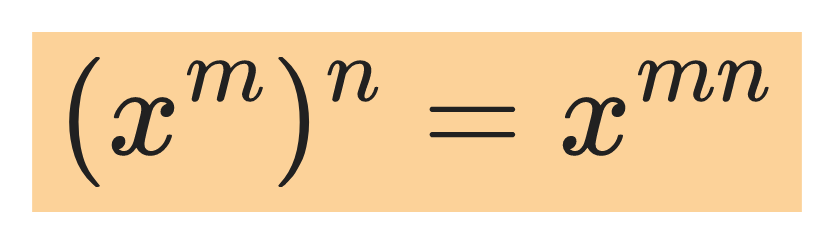
For example:

Other power rules:
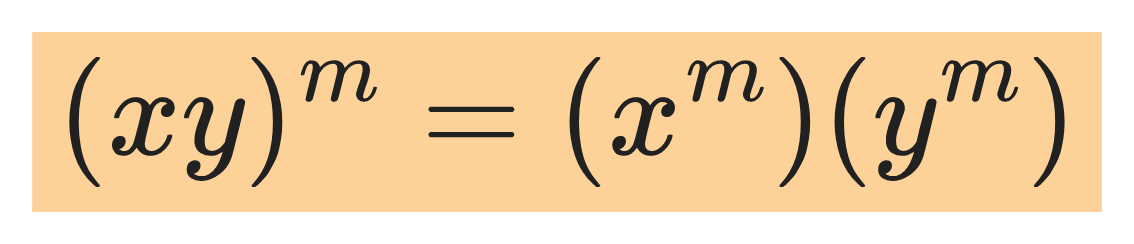

Example 1.1
Simplify the expression:
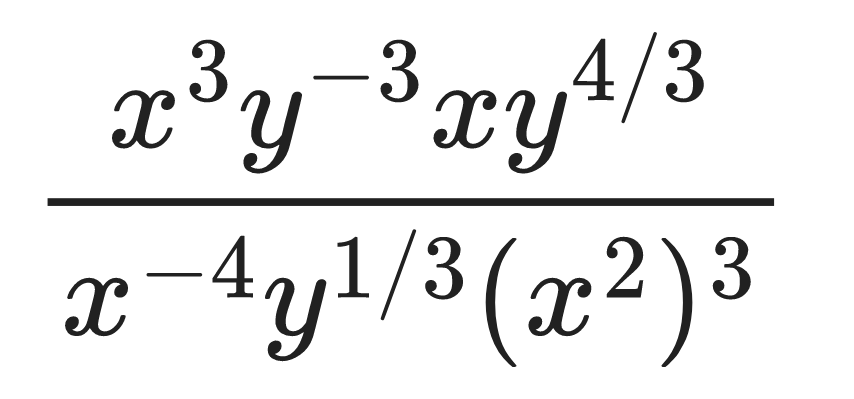
Solution


Therefore,

1.2 Scientific Notation and Powers of 10
A quantity is said to be in scientific notation if it is expressed as a decimal number with one digit to the left of the decimal point, multiplied by the appropriate power of 10.
The general way of representing numbers in scientific notation is:
x × 10ʸ
where: 1 ≤ x < 10
Example: 6.3 × 10⁴ is expressed in scientific notation.
If y (the power of 10) is positive, then the decimal point is moved to the right y times to obtain the fully written out number. Thus 6.3 × 10⁴ = 63,000
If y (the power of 10) is negative, then the decimal point is moved to the left y times to obtain the fully written out number. Thus 6.56 × 10⁻³ = 0.00656
Multiplying and Dividing in Scientific notation
To multiply (or divide) in scientific notation, multiply (or divide) the decimal parts to get the decimal part of the result and multiply (or divide) the powers of 10 to get the power-of-10 portion of the result.
Example 1.2
(8.43 × 10⁸) (2.21×10⁻⁵)
= (8.43 × 2.21) (10⁸×10⁻⁵)
= (18.6) × (10⁸⁻⁵)
= 18.6×10³
= 1.86×10¹×10³
= 1.86×10⁴
Similarly,
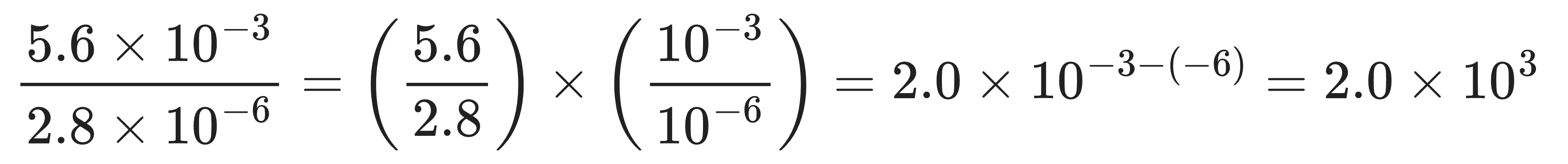
1.3 Algebra
Solving Equations
An equation consists of an equal sign and quantities (represented by symbols) to its left and to its right.
Every equation tells us that the combination of quantities on the left of the equals sign has the same value as (that is, equals) the combination on the right of the equal sign.
To solve an equation means to assign a value to a symbol in an equation which is considered to be unknown or to express that quantity in terms of other quantities.
The following rule is used in solving equations:
An equation remains true if any valid operation performed on one side of the equation is also performed on the other side.
The operations could be (a) adding or subtracting a number or symbol, (b) multiplying or dividing by a number or symbol, or (c) raising each side of the equation to the same power.
Example 1.3
Solve for a in the equation below:
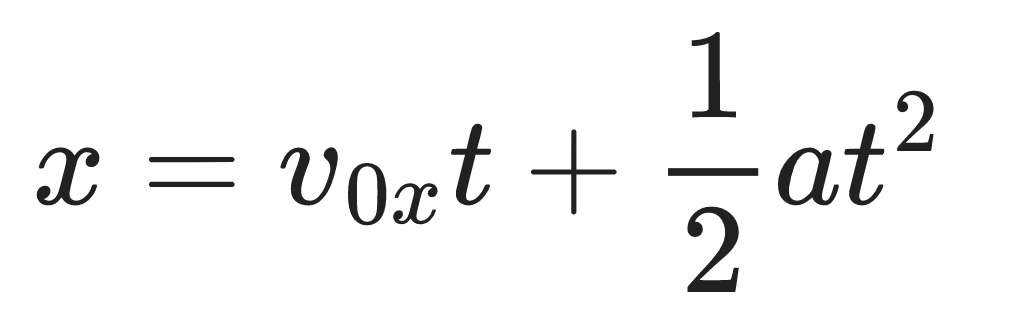
Solution
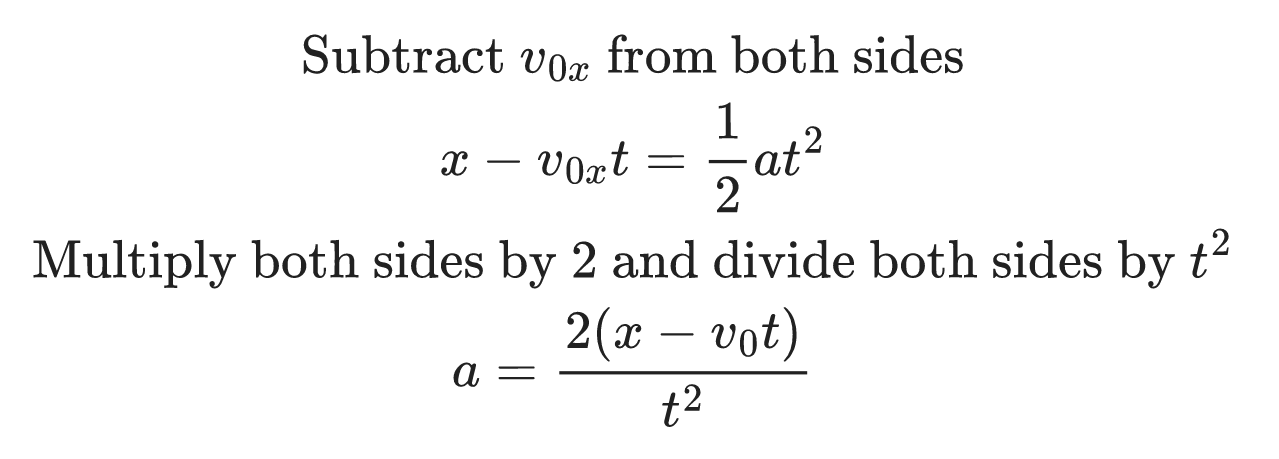
The Quadratic Formula
Equations in the form ax²+bx+c=0 where a, b and c are all non-zero are called quadratic equations.
Its solutions are expressed by the quadratic formula:
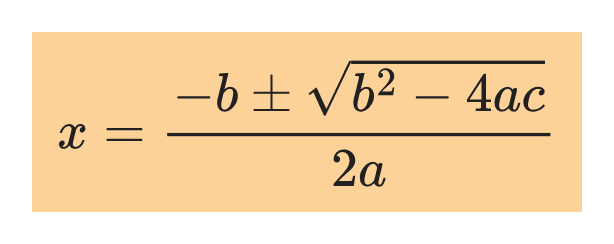
In general, a quadratic equation has two roots (solutions), which may be real or complex numbers.
When b²−4ac = 0, then the roots are equal and real numbers.
When b² > 4ac, that is, b²−4ac is positive, then the two roots are unequal and real numbers.
When b² < 4ac, that is b²−4ac is negative, then the roots are unequal complex numbers and cannot represent physical quantities. In such a case, the quadratic equation has mathematical solutions, but no physical solutions.
Example
Find the values of x that satisfy the equation:
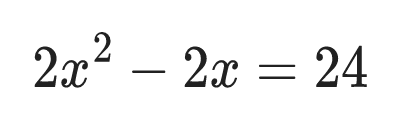
Solution

Simultaneous Equations
Simultaneous equations are independent equations that share unknowns which are solved together.
To solve a simultaneous equation in two unknowns x and y:
Solve for an equation for x in terms of y and then substitute the result into the second equation to obtain an equation in which y is the only unknown.
Solve this new equation for y and substitute the value of y in the equation for x to get the value of x.
Example
Solve the following equations for x and y.

Solution-
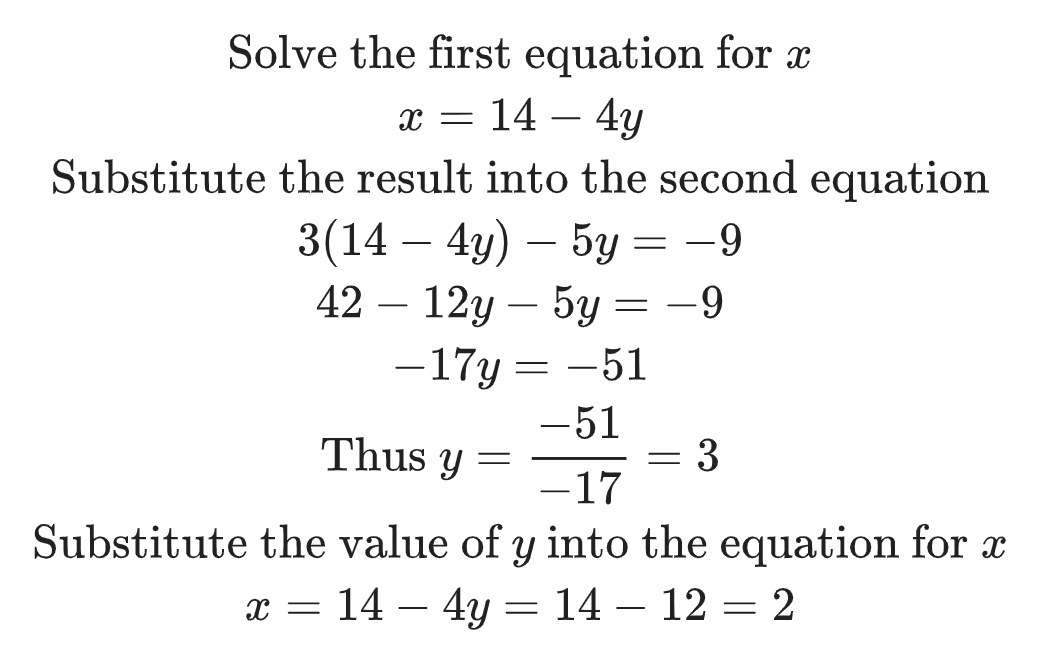
Another way of solving such equations is to combine them to eliminate one of the common unknowns.
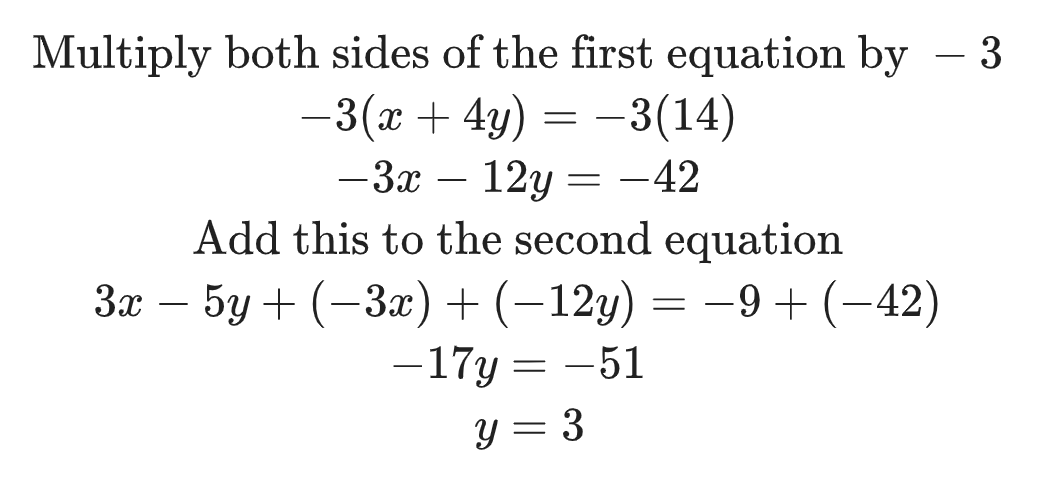
1.4 Direct, Inverse, and Inverse-Square Relationships
Physical quantities often have verifiable relationships.
Direct relationships
y ∝ x (read as y is directly proportional to x) means an increase in y cause as increase in x by the same factor.
The ratio y/x is a constant, say, k. That is,

Example C ∝ d i.e., the circumference of a circle is directly proportional to its diameter. The ratio C/d is a constant known as π (pi) i.e., C/d is always 3.14.
C=πd
Graph of Direct Proportionality Relationship
When y ∝ x, y=kx, the graph of y versus x is a straight line through the origin.
A graph showing a direct relationship between y and x. In the graph, the change of the quantity x is labeled as Δx (which is often called “run”) and the corresponding change in y is labeled as Δy (which is often called “rise”).
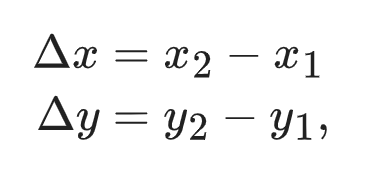
where (x₁, y₁) and (x₂, y₂) are coordinates of the two points on the line.
The constant of proportionality between Δy and Δx is also k.
Thus

The steepness of the line is measured by the ratio Δy/Δx and is called the slope of the line. Thus,
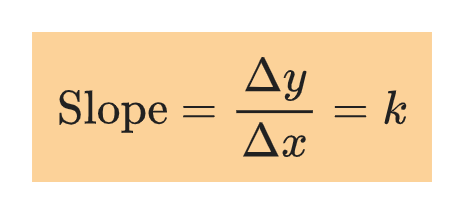
The slope of a line can be positive, negative, zero, or undefined.
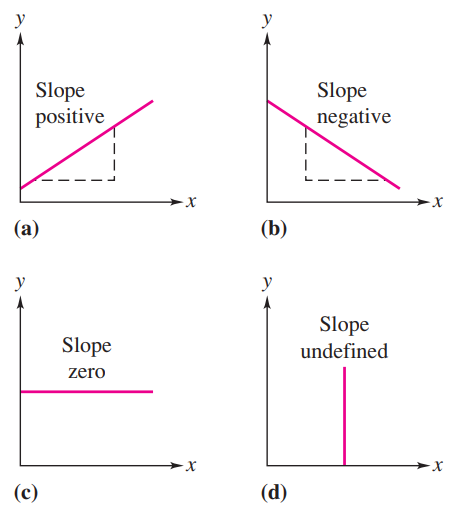 Example
Example
If y is directly proportional to x, and x=2 when y=8, what is y when x=10?
Solution

Inverse Proportion
y ∝ 1/x (read as y inversely proportional to x) means an increase in y causes a decrease in y such that the product xy remains constant. That is when x changes from x₁ to x₂ y changes from y₁ to y₂ so that x₁y₁=x₂y₂=k
A graph showing an inverse relationship between y and x.
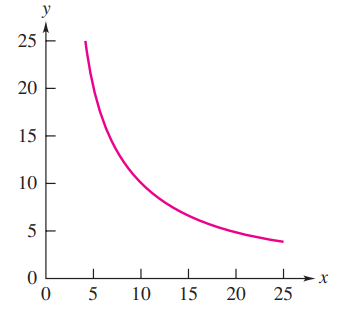
Inverse Square Proportion
If y varies inversely as the square of x, then:
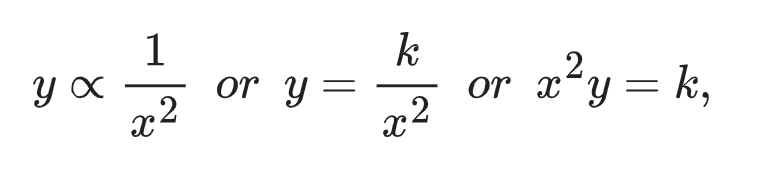 where k is the constant of proportionality.
where k is the constant of proportionality.
A graph showing an inverse square relationship between y and x.
1.5 Logarithmic and Exponential Functions
The base-10, or common logarithm (log) of a number y is the power to which 10 must be raised to obtain y:
y=10ˡᵒᵍʸ
Example: 1000=10³, hence log (1000) = 3; you must raise 10 to the power 3 to obtain 1000.
Inverse of Logarithm
We can be given the log of y and asked to find y.
Thus, if log y = x and x is given, what is y?
log y = x. Then y = 10ˣ
If log y = - 2.0, what is y? y = 10⁻²
NB: log y = +ve if y > 1 log y = -ve if 0<y<1
Aside from 10, another base that occurs frequently in Physics is the quantity e = 2.718…
The natural logarithm (ln) of a number y is the power to which e must be raised to obtain y: x = eˡⁿʸ
then y = eˣ, known as the exponential function
The plot of eˣ is shown below

The exponential function and natural logarithm occur in natural phenomena such as radioactive decay where the rate of increase or decrease of some quantity depends on the quantity.
Rules of logarithms

A particular example of the second rule:

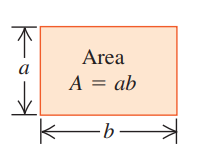
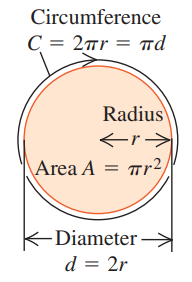
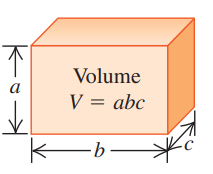
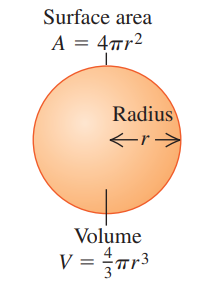
1.6 Areas and Volumes
Geometric Shape | Formulae |
|---|---|
Rectangle |
|
Circle |
|
Cuboid |
|
Sphere |
|
Cylinder |
|
1.7 Plane Geometry and Trigonometry
Some useful results about angles:
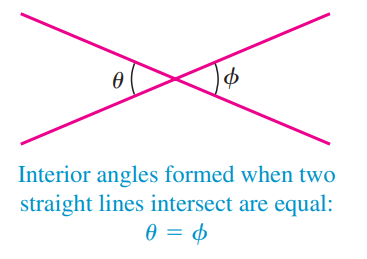
1. Vertically opposite angles |
|
|---|---|
2. Alternate angles |
|
3. |
|
4. Linear pair of angles |
|
Similar Triangles
Similar triangles have equal corresponding angles and equal ratios of corresponding sizes.
If the two triangles in the diagram below are similar, then:

Congruent Triangles
Two similar triangles of the same size are said to be congruent.
If two triangles are congruent, one can be flipped and rotated so that it can be placed precisely on top of the other.
Right-triangles and Trig functions
A right-triangle has one angle that is equal to 90º.
The Pythagorean theorem applies to right-triangles.

Trigonometric functions
Similarity between right triangles allows us to define the trigonometric functions which are ratios of a pair sides.
These depend only on one of the angles in the right angle.
The sine, cosine and tangent of an angle θ are as follows:

Angles may be expressed in either degrees or radians, where π radians = 180º
Inverse trig functions denoted by sin⁻¹ x or arcsin x, cos⁻¹ x or arccos x, tan⁻¹ x or arctan.
sin (30) = 0.500. sin⁻¹ (0.500) = 30
Example
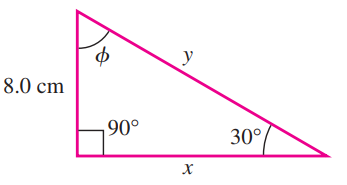
A right triangle has one angle of 30º and one side with length 8.0 cm as shown:
What is the angle ϕ and what are the lengths x and y of the other two sides of the triangle.
Solution

In a right triangle, the angles range from 0º to 90º, and the trig functions are all positive
For other applications such as resolving a vector, it is useful to define the trig functions for angles outside the range.
Graphs of sinθ and cosθ are given below:
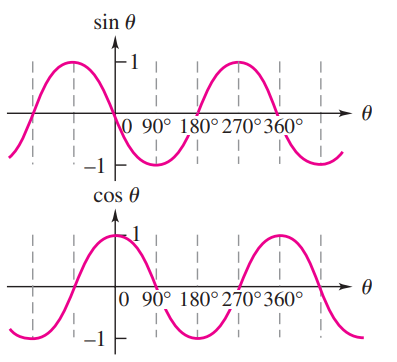
Comparing the graphs of sinθ and cosθ
The values of sin and cos vary between +1 to -1
Each function is periodic, with a period of 360º.
The two functions sinθ and cosθ are 90º out of phase.
When one is zero, the other has maximum magnitude.
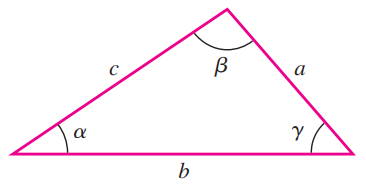
Laws of sines and cosines
For any triangle, the two relations below apply:
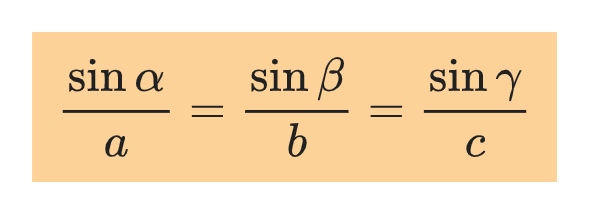
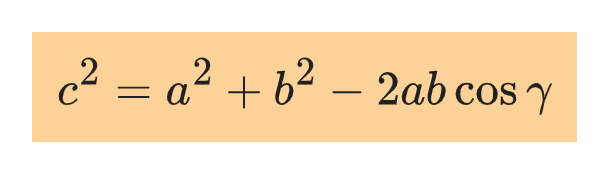
Useful trigonometric identities