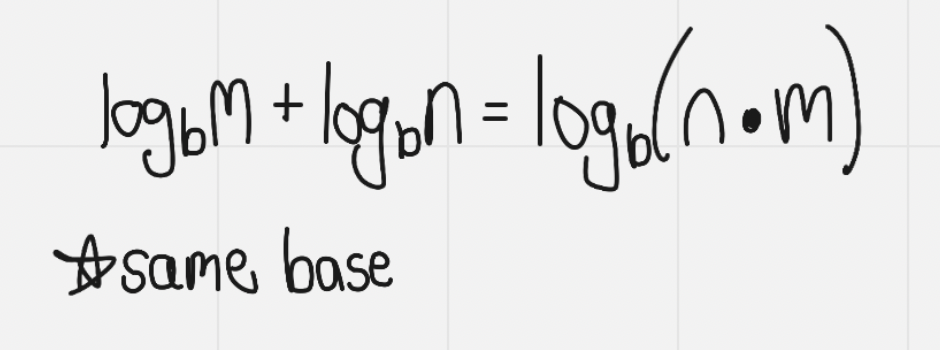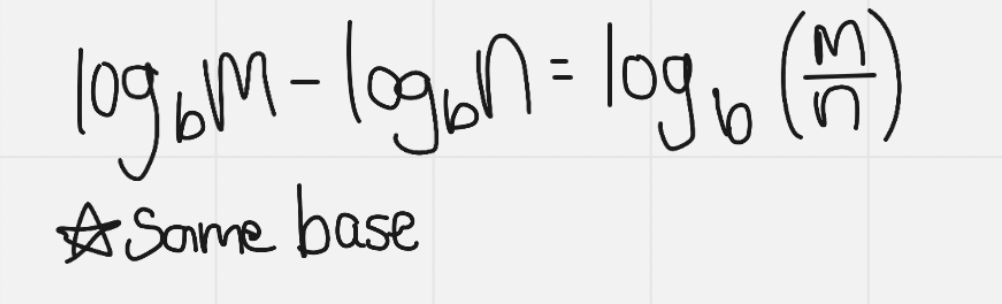12-07: Logarithms (II)
Drop the Base
You can solve same bases’ exponents by dropping the bases
May need to make things into the same base
If you can, make the bases the same as a power of the smallest base if possible (power of a power rule)
Exponential Growth and Decay
% Growth/Decay
A = A₀(1± r)
A: final quantity
A₀: initial quantity
r: growth/decay rate (express as a decimal)
Doubling
A = A₀(2)ᵗ/ᵈ
A: final quantity
A₀ : initial quantity
t: time passed
d: doubling time (how long it takes to double)
Half life
A = A₀(1/2) ᵗ/ʰ
A: final quantity
A₀ : initial quantity
t: time passed
h: half life (how long it takes to half in quantity
Note: time units must be the same
Product Law of Logs
Quotient Law of Logs
Techniques for Solving Log Equations
If just a single log term on either side of the equal sign → cancel logs

If both log terms and constants in an equation → rearrange, logs on one side and constants on the other
When +/- log terms → combine with product and quotient laws (above)
Change to exponential form:
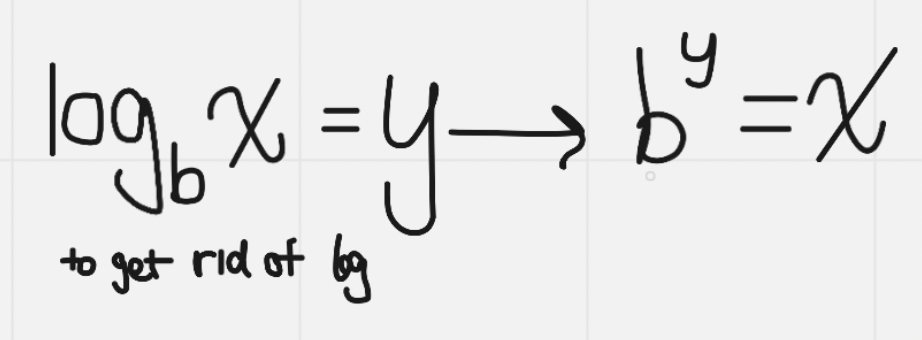
Check for extraneous roots
Extraneous root: answer that throws error when plugged into the question
Cannot log 0 or a negative numbers → sub answers back in to check
Should be greater than 0 when checking (make expression >0 when checking and if it works then it doesn’t break the domain)