Math 2 Reviewer

Quadrilaterals

• a four-sided polygon

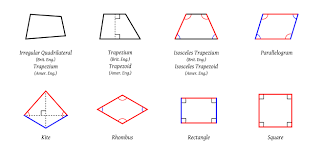
Parallelogram

• a quadrilateral with 2 pairs of parallel sides.

Rhombus

• has 4 congruent sides

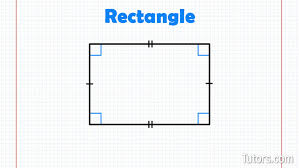
Rectangle

• has 4 right angles

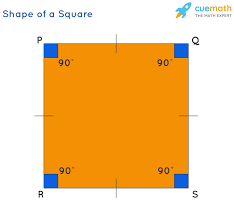
Square

• has both 4 congruent angles and 4 right angles

Quadrilateral Angle-Sum Theorem

• the sum of the measures of the interior angles of a quadrilateral is 360 degrees

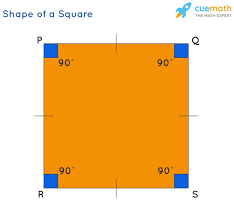
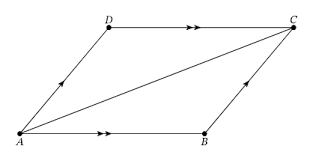
Properties of Parallelograms

if a quadrilateral satisfies any of the conditions, then it is a parallelogram

1) Both pairs of opposite sides are parallel

2) Both pairs of opposite sides are congruent

3) Both pairs of opposite angles are congruent

4) The consecutive angles are supplementary

5) A pair of opposite sides are both parallel and congruent

6) The diagonals bisect each other

7) Each diagonal divides a parallelogram into 2 congruent triangles

Special Parallelograms

Rectangle

• the diagonals of a rectangle are congruent

Rhombus

• the diagonals of a rhombus are perpendicular

Square

• the diagonals of a square are both congruent and perpendicular

TRAPEZOIDS

• a quadrilateral with a pair of parallel sides

Theorem 1:

• the median of a trapezoid is parallel to its bases, and its length is half the sum of the length of the bases

Isosceles Trapezoid

• a trapezoid with congruent legs

Theorem 2:

• the base angles of an isosceles trapezoid are congruent

Theorem 3:

• the diagonals of an isosceles trapezoid are congruent

Midline theorem(Triangles Only)

• the midline(midsegment) of a triangle is parallel to the base of the triangle and its length is half as long as the base

KITE

• a quadrilateral with 2 pairs of adjacent sides that are congruent, and no opposite sides are congruent

• consecutive sights with equal length.

Theorem 1:

• the diagonals of a kite are perpendicular

Theorem 2:

• a kite has exactly one pair of opposite angles that are congruent

Theorem 3:

• the diagonal through the vertex angles(angles up&down) bisects the vertex angles(angles left&right) and the other diagonal

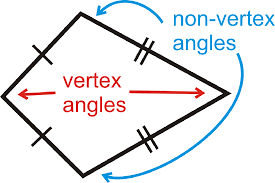
Solving

Pythagoream theorem
ax²+b²=c²

Use to identify diagonal’s measurements.

Median Formula

b1+b2/2 = median