2.2: Data Transformations and Z-Scores

Data Transformations

• Measures of center include the mean, median, quartiles, minimum, and maximum of a set of data
• Measures of spread include the IQR, range, and standard deviation
• When a constant is added to every number in a list,
    * The measures of center increase by that amount and the measures of spread remain the same
• When every number in a list is multiplied by a constant,
    * The measures of center are multiplied by that amount and the measures of spread also get multiplied by that amount

Comparing Unalike Figures

• Suppose we have two values that we want to compare, but they don’t come from the same distribution
    * Eg. getting a 610 on SAT math vs. a 24 on ACT math
    * Eg. being a 80” guy vs. a 76.5” girl
• We can compare these figures by getting a standardized score called a z-score
    * z = (x-μ)/σ
      * z: z-score
      * x: value
      * μ: population mean
      * σ: population standard deviation
• A z-score shows exactly how many standard deviations above or below the mean a value is
• Even if two data points come from different distributions, they can be directly compared if converted to z-scores
• When comparing two z-scores, the higher z-score is the better relative score

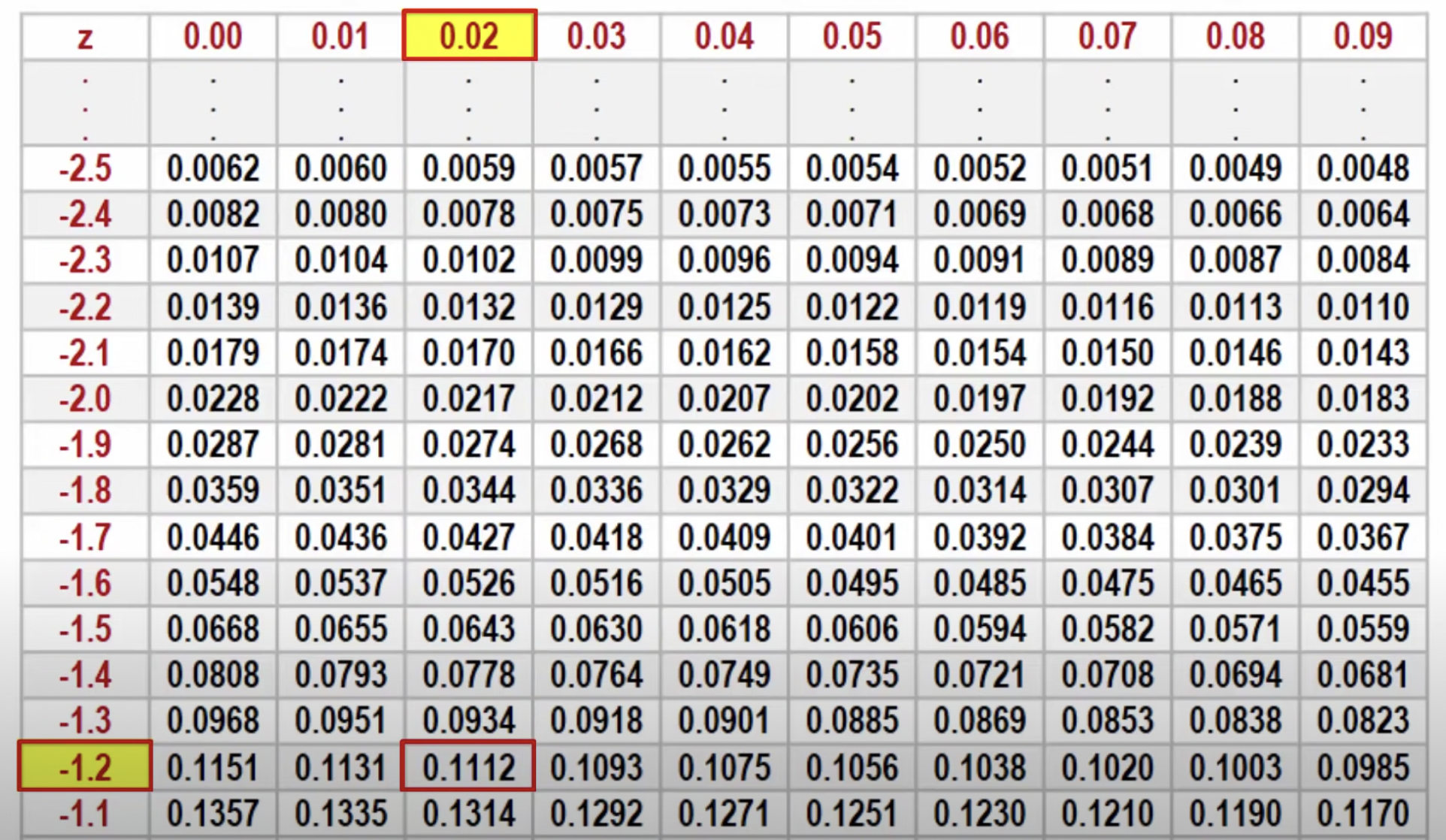
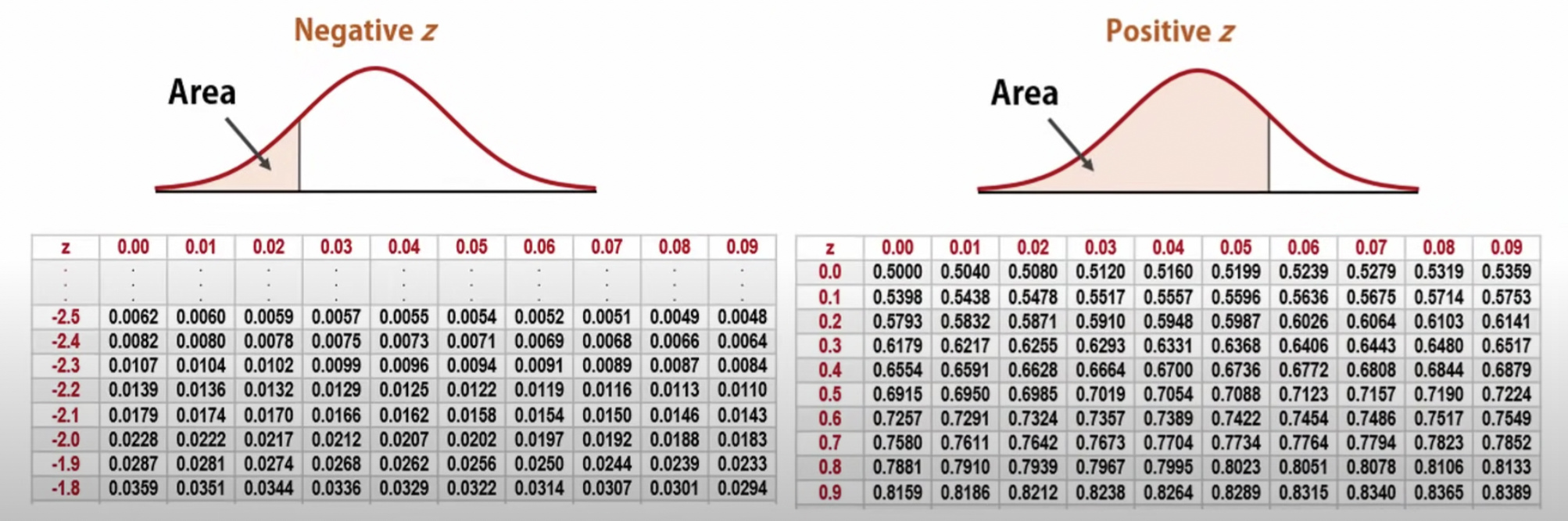
Z-Charts

• A chart which can be used to convert proportions to z-scores and vise-versa
    * Available on the “cheat sheet” during the AP exam

Example Problem

• Find percent of values less than 54
    * μ = 65
    * σ = 9
• X~N (μ,σ) → Z~N (65,9)
• Finding P(x<54) → x = 54, put into equation z = (x-μ)/σ

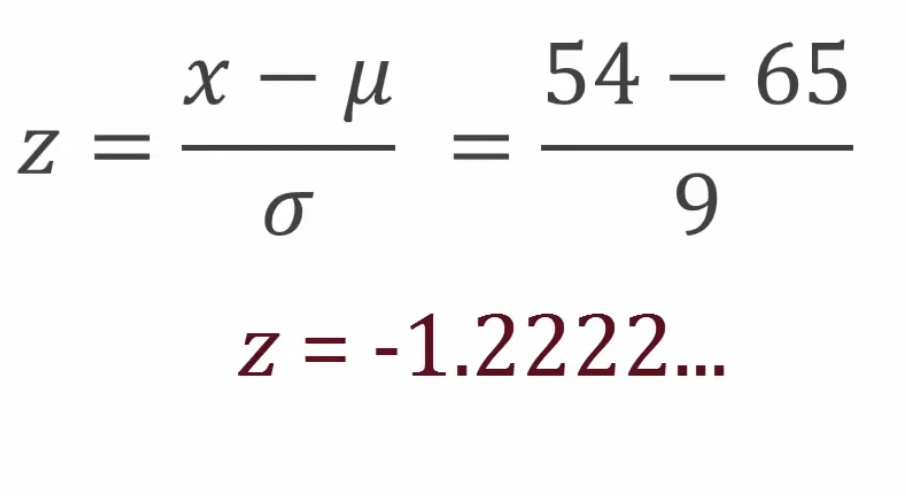
• Locate z = -1.2222 on z-chart
    *
• P(x < 54) = P(z < -1.22) = 0.1112 (11.12%)