Introductory Chemistry Midterm Study Guide >
Scientific method
The scientific method involves observing/collecting data, forming hypotheses, experimenting, and then forming theories backed up by the data.
(1)Observation is describing and using your senses to gather information. This can be quantitative, meaning numerical data, or qualitative, which is descriptive data. The scientist then uses the gathered data to form a (2)hypothesis, which is a testable statement. Using the hypothesis, people can then begin (3)testing through experimentation, to obtain the data needed to support or refute the claim. (4)Theorizing can then begin, this process typically involves the use of models to help demonstrate or explain the phenomena, and find any correlations. From this, scientists can form theories or broad generalizations that give an explanation.
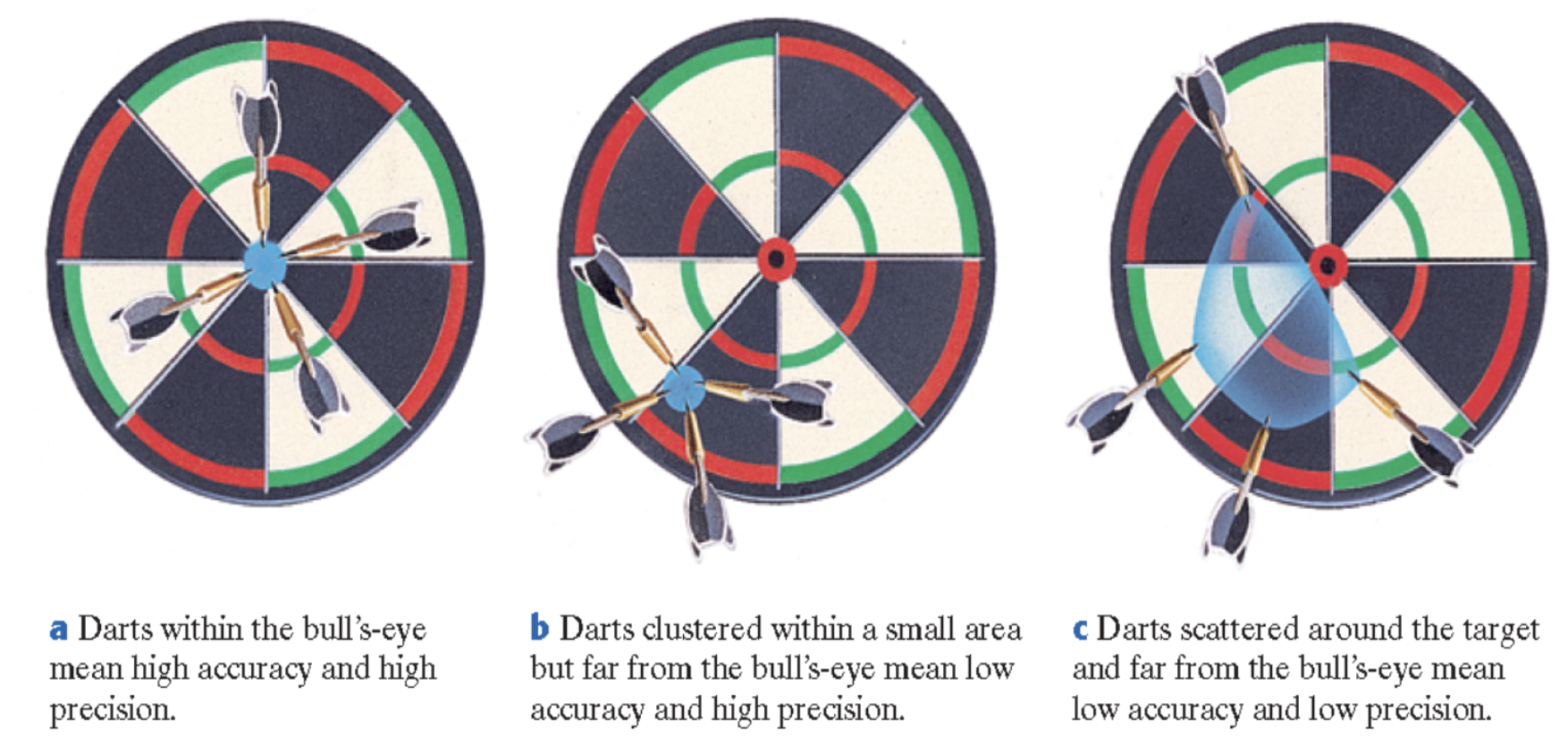
Accuracy vs. Precision
Accuracy is the closeness of a measurement to the actual or true value of something, while precision is defined as the closeness of the measurements to one another.
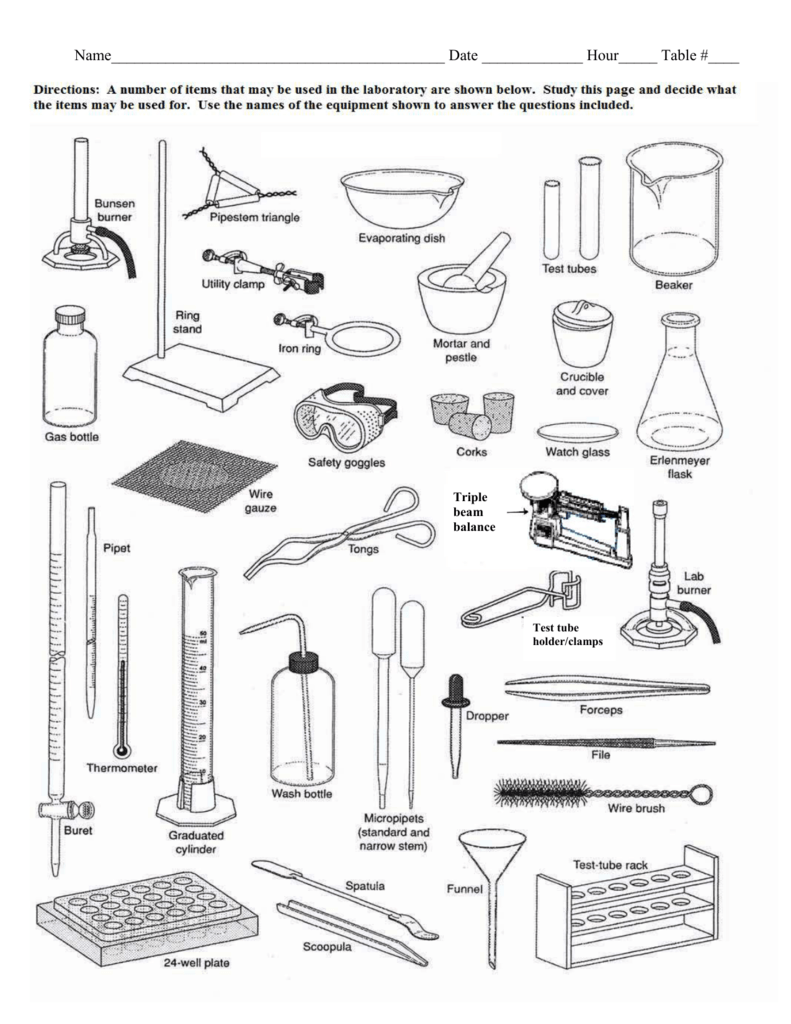
Lab tools
Scientific notation and significant figures
Really large or small numbers can be difficult to keep track of for scientists, so they use scientific notation to express numbers through the product of a coefficient and the number 10 raised to a power. When using this method, the coefficient must be greater than or equal to 1, but less than 10. So for example, if you had the number 56,000 your coefficient would be 5.6, and it would be multiplied by 10^4, so 5.6 x 10^4. If you had the number 0.000056, your coefficient would be 5.6, and it would be multiplied by 10^-5, (negative due to the fact that you are moving to the right) so 5.6 x 10^-5.
Significant figures are used for the precision of a number because if we express a number that has more digits than the actual measured value, it can be seen as less accurate.
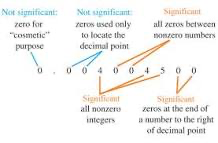
5 basic rules for identifying significant numbers
All nonzero digits are significant
The zeroes in between nonzero digits are significant
Zeroes to the left of the first nonzero digits are insignificant
All zeroes to the right of a decimal point and a number are significant
Zeroes to the end of the number but not to the right of a decimal point are not significant
When multiplying and dividing with significant numbers, you count the number of significant figures in each number and choose the least amount. Then, you multiply or divide normally and the product should be rounded to that minimum number of significant digits.

When adding or subtracting with significant figures, you see which number has the least digits. After adding/subtracting the two numbers, you then round your final answer to the number of decimal places that you counted earlier.

Units scale and units conversion
| Giga (G) | 1,000,000,000 |
|---|---|
| Mega (M) | 1,000,000 |
| Kilo (k) | 1,000 |
| Hecto (h) | 100 |
| Deka (da) | 10 |
| Base (Meter, Liter, Gram) | 1 |
| Deci (d) | 0.1 |
| Centi (c) | 0.01 |
| Milli (m) | 0.001 |
| Micro (µm) | 0.000001 |
| Nano (n) | 0.000000001 |
1ft = 30.48 cm
1 inch = 2.54 cm
1 calorie = 4.184 joules
Specific heat of water = 4.184
1 Calorie = 1000 calories
1 Kilowatt-hour = 3.60 x 10^6 Joules
Density calculations
D (density) = m (mass) / v (volume)

Percent error calculation

Practice Question:
Calculate the percent error if the density of alcohol (ethanol) is found to be 0.802 g/mL but the true value is 0.798 g/mL
Answer: 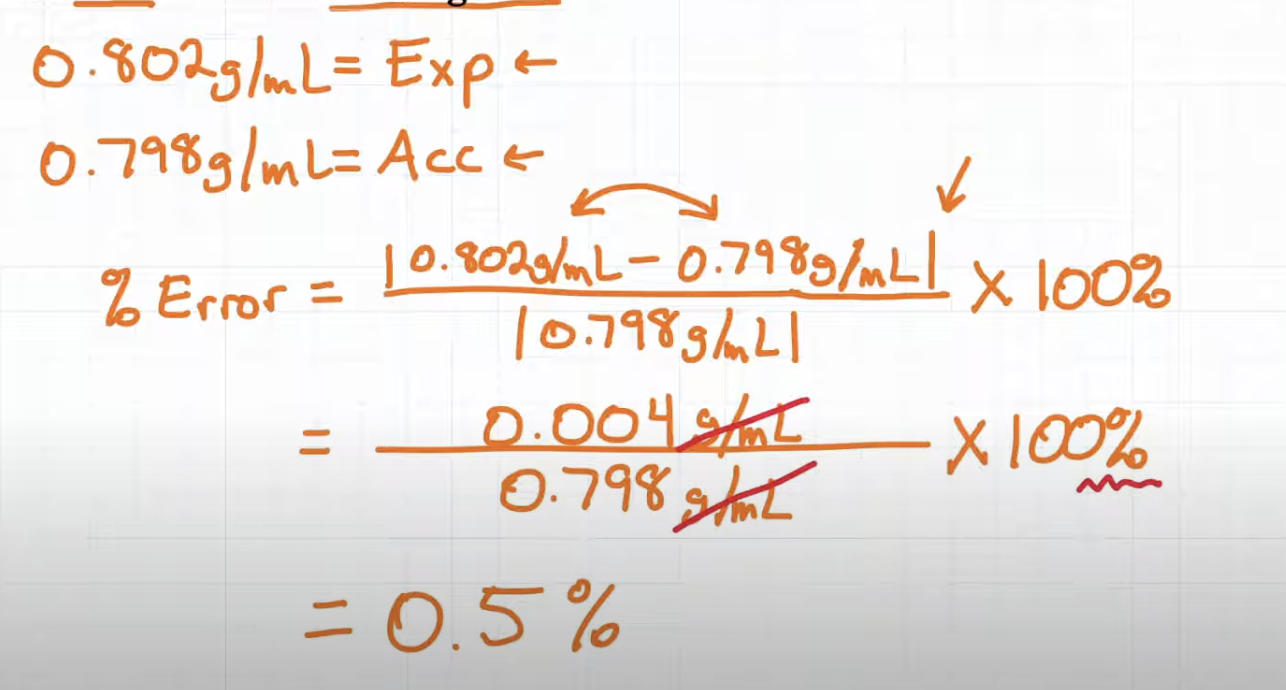
Matter classification and separate techniques
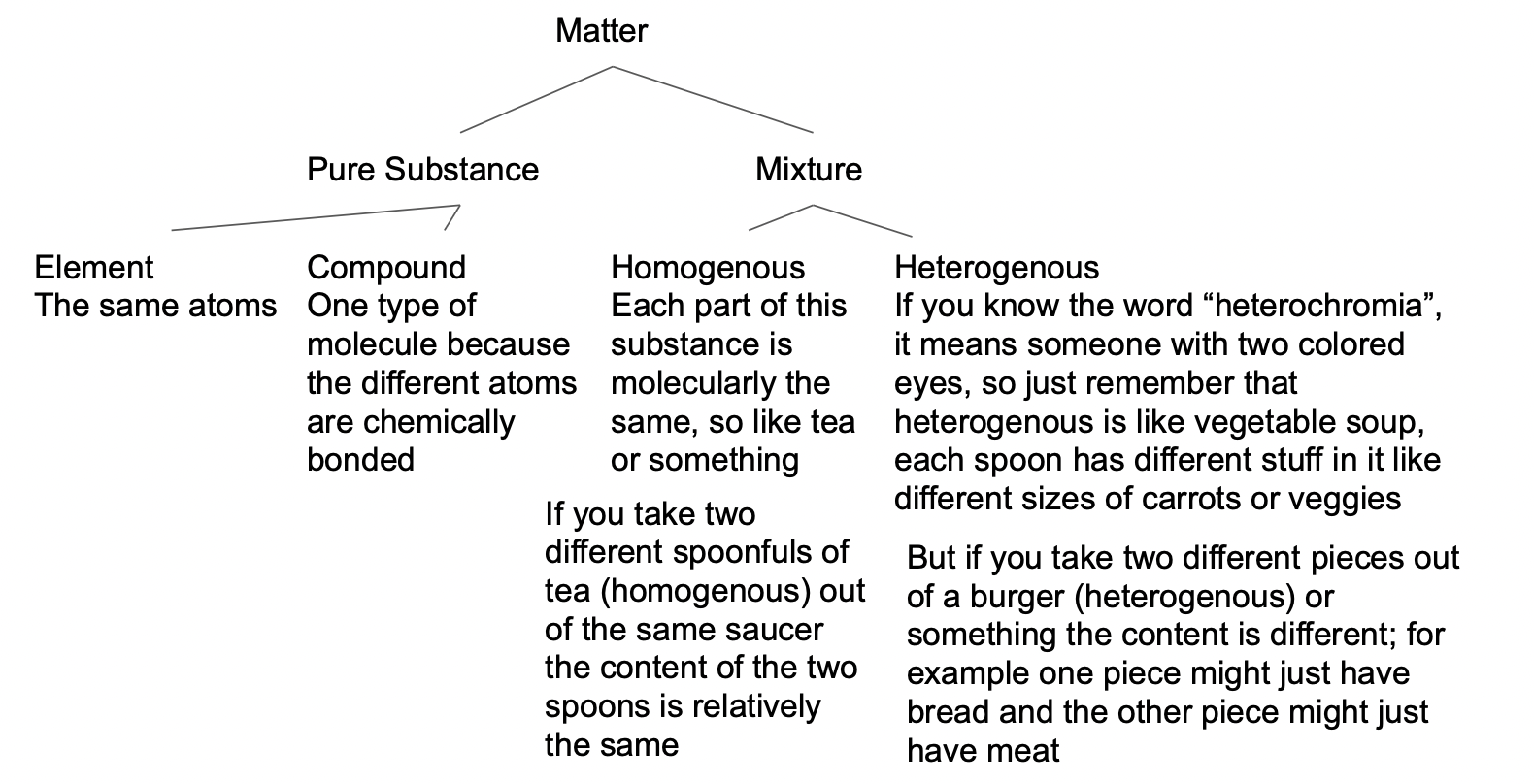
Physical vs. Chemical Change
Physical
-Change of shape/size
-Change in state
Chemical Change
-Difficult to revert (Cooking an egg is a chemical change because it is difficult to change back to uncooked)
-Usually a state change
-Color change
-Odor
-Temperature change
-Precipitate
-Bubbles
-Light emission

Separation techniques:
☆Centrifugation
Using a centrifuge to separate particles in a liquid, or molecules with different densities, by spinning them at a high speed. Examples: extracting fat from milk, separating heterogeneous mixtures
-solids from liquids, liquids from liquids
☆Chromatography
The process of using chemical properties to separate substances, this can show you what makes up a solution because the substances all move at different speeds up the medium used.
-liquids from liquids
☆Decanting
When you pour the top of a mixture
-liquids in liquid, solids in liquids
☆Distillation
Using evaporation or condensation through heating
-separating liquids from liquids, solids from liquids
☆Filtration
Using a filter, or a material with minuscule holes to separate liquids and solids
☆Evaporation/boiling
Using heat to change a liquid to a gas, in order for it to leave behind the solute dissolved in it.
The energy of three states of matter comparing, energy types, and thermal energy calculations
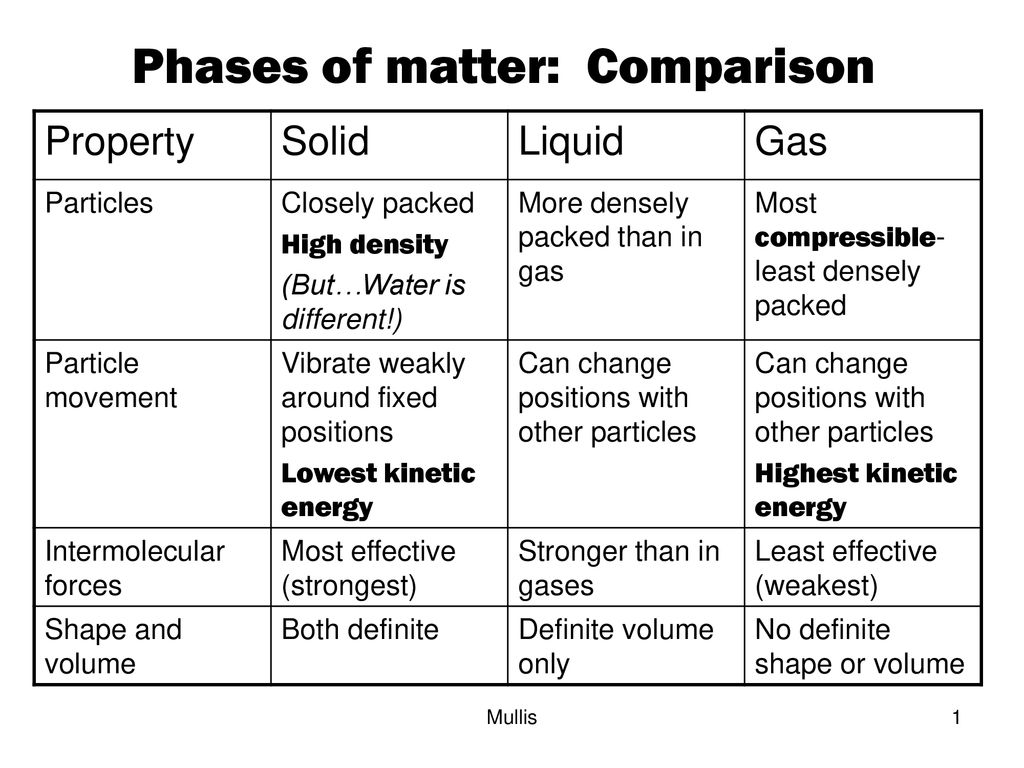
Thermal Energy Formula:

Practice Problem: A car with magnesium wheels is parked in the sun. If the temperature rises from 22C to 35C how much MJ of heat does each 6.8 kg wheel absorb? (C= 1.02 J/gC) 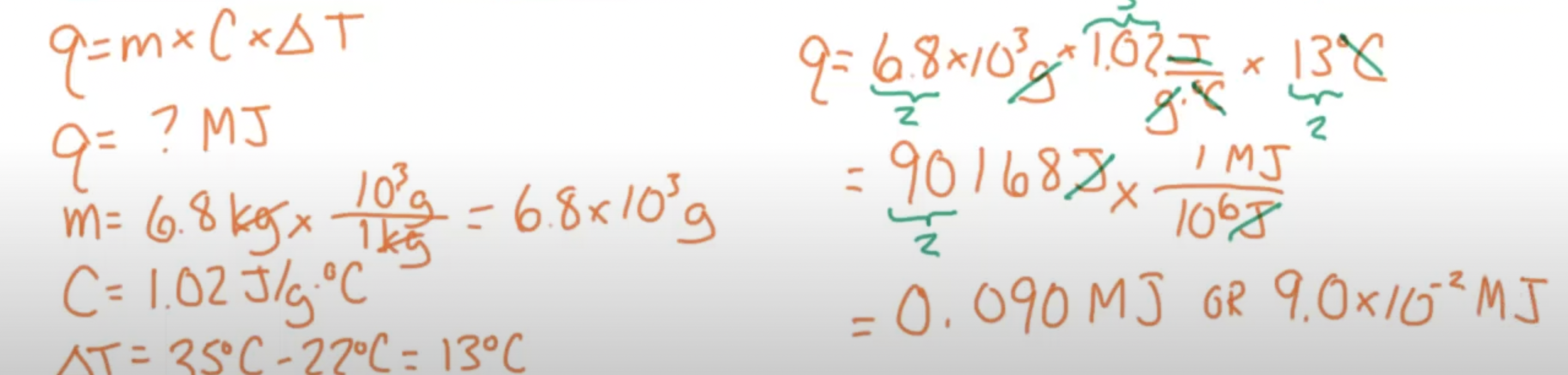
Atomic theory and related famous experiments
The atomic theory states that all matter is composed of small particles called atoms, and states: all matter is made up of invisible and indestructible particles called atoms, compounds are made up of 2 or more kinds of atoms, and that the atoms of an element are identical in size, mass, and other properties.
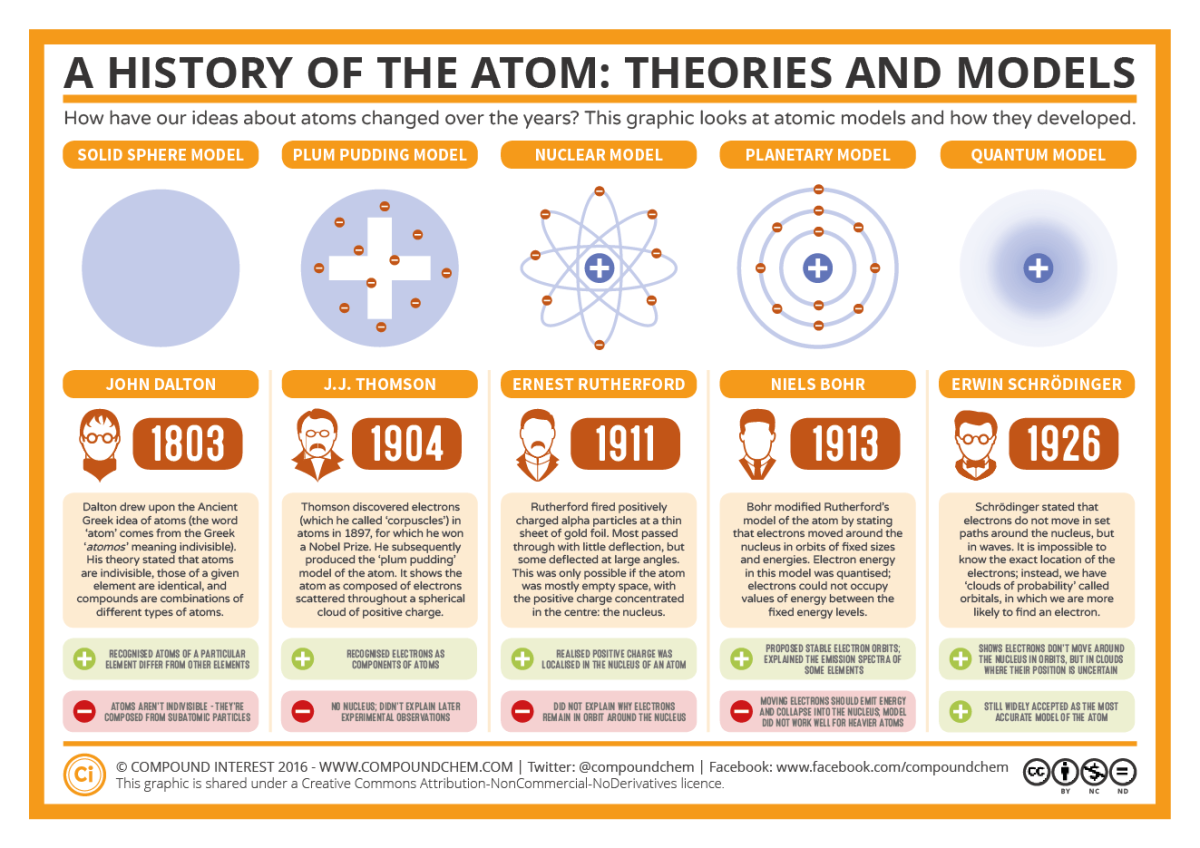
Isotopes vs. ions
an ion is an atom or molecule with a charge, while an isotope is a form of an element with a different number of neutrons, therefore having a different mass number as well.
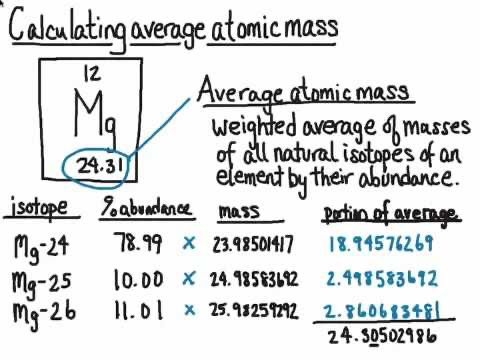
Average atomic mass
can be found displayed on the periodic table, and describes the average mass of naturally occurring atoms of that element.
This can be calculated by adding the product of each isotope’s percent abundance and atomic mass.
Radioactive decay and balanced nuclear equations
Radioactive decay occurs when an unstable nucleus gives off radiation/energy to reach a more stable state. To show this, we use nuclear equations which must be balanced, to demonstrate the law of conservation of mass properly.
Particles and their symbols:
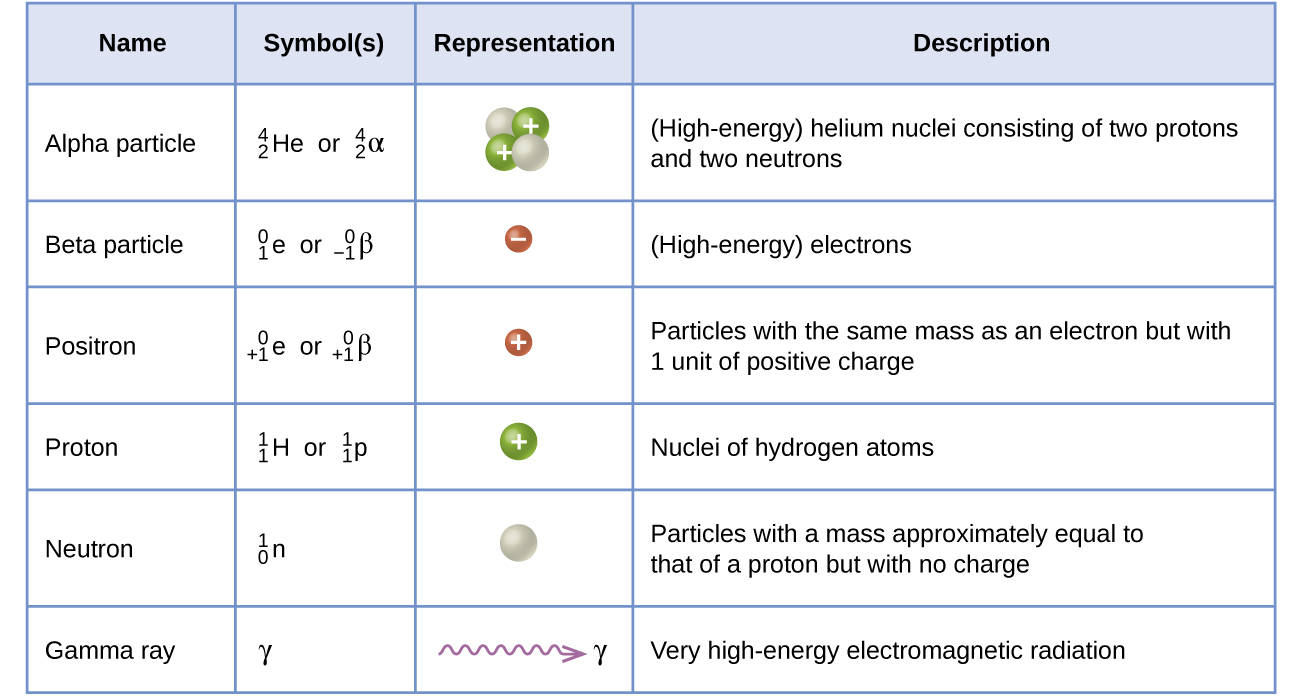
and
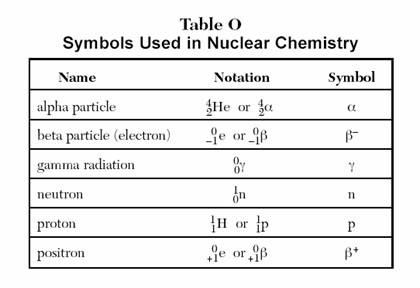
Below is a nuclear equation, it represents the reactants and products in radioactive decay.

Practice Problem:

Answers:
A
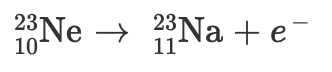
B
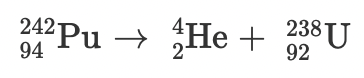
C 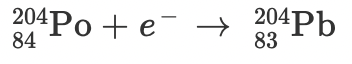
Half-life calculation
Half-life is the time it takes for a quantity of a radioactive sample reduce to half.

Example:

Properties of light and light energy calculations
λ (lambda) = wavelength
A wavelength is the distance between where a wave’s shape repeats. In other words, it is the distance from crest to crest (Top to top) or trough to trough (bottom to bottom). An example is included in the diagram below.
ν (nu) = frequency
The frequency is the number of waves repeated over a certain unit of time, waves with high frequency have shorter wavelengths, and this is the opposite for low-frequency waves.
C= speed of light
The speed at which light propagates through certain materials. In the air, the speed of light is:
<<3 × 10^8 m / s<<
E= energy
h= Planck’s constant
Planck’s constant is a fundamental foundational constant in quantum mechanics-
<<6.626 x 10^-34<<
<<C = λ x ν<<
Speed of light = wavelength x frequency
<<E = h x ν<<
Energy = Planck’s constant x frequency
<<E = h c/λ<<
Energy = (Planck’s constant x Speed of light ) / wavelength
Periodic table information and valence electron
https://knowt.io/note/8fd6753b-4120-44eb-99ac-1bfbec78d869/Unit-5-The-Periodic-Table
Endothermic and Exothermic
Exothermic is when a reaction releases energy, it typically gets hotter, while endothermic does the opposite and absorbs energy, getting colder. Anabolic reactions are endothermic, while catabolic reactions are exothermic.
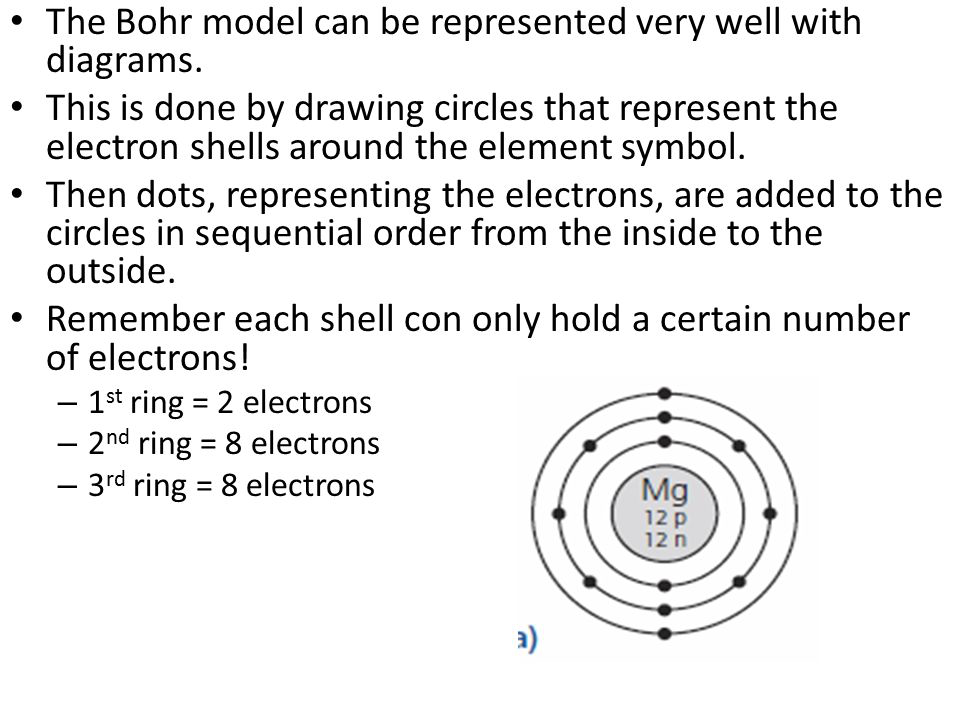
Bohr model and line spectrum
The Bohr model is a system that consists of a nucleus surrounded by orbiting electrons. It explains how electrons move through orbits when they gain energy and return back to their ground state with the emission of light, and loss of energy.
Line Spectrum
Different elements have varying line spectrums, which is observed when these pure samples are heated. As an example, if you heat a sample of hydrogen gas at low pressure, it emits a red light. This color is one of the few lines shown on the line spectrum diagram, depicting the range of wavelength of light that can be emitted or absorbed.