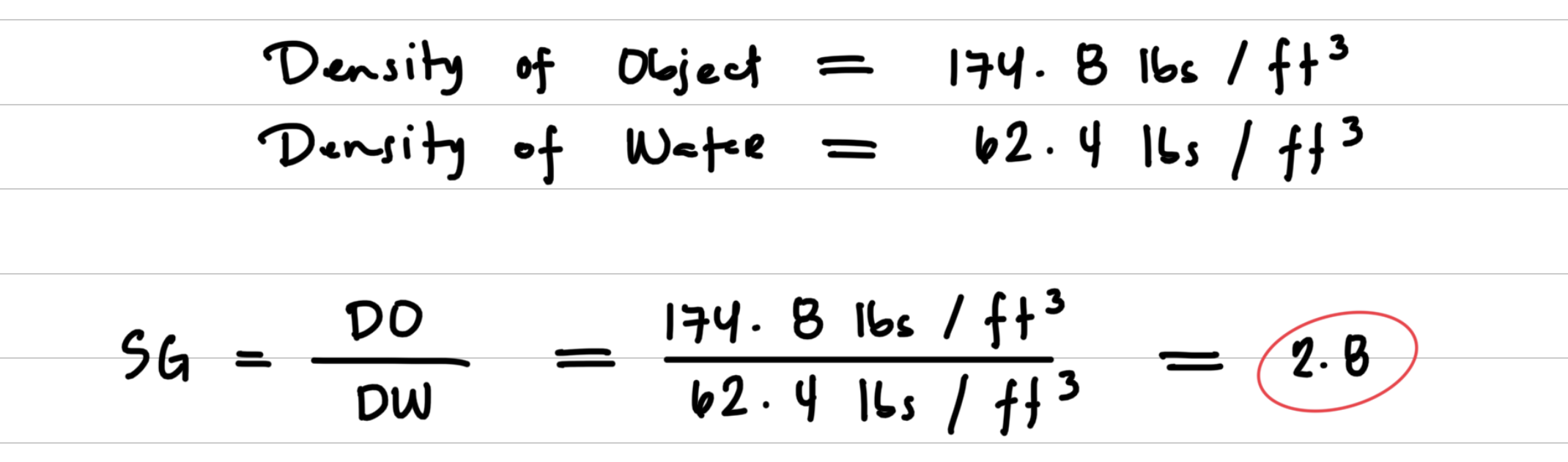Chapter 2: Chemistry and Measurements
2.1: Units and Measurements
- Metric System: A system of measurement used by scientists and in most countries of the world.
- International System of Units (SI): Also known as Système International; the official system of measurement throughout the world except for the United States.
Units of Measurement and their Abbreviations
| Measurement | Metric | SI |
|---|---|---|
| Length | meter (m) | meter (m) |
| Volume | liter (L) | cubic meter (m3) |
| Mass | gram (g) | kilogram (kg) |
| Temperature | degree Celsius (°C) | kelvin (K) |
| Time | second (S) | second (S) |
Length
- The metric and SI unit of length is the meter (m).
- A meter is 39.4 inches, which makes it slightly longer than a yard.
- A centimeter (cm) is a smaller unit of length and is commonly used in chemistry.
Volume
- Volume: The amount of space a substance occupies.
- The metric and SI unit of volume is the liter (L).
- Millimeter (mL) is a smaller and more convenient unit of volume, mostly used by chemists at laboratories or hospitals.
Mass
- Mass: The measure of the quantity of material it contains.
- The SI unit of mass, the kilogram (kg) — used for larger masses.
- Gram (g) is used for smaller masses.
- Weight: The measure of the gravitational pull on an object.
Temperature
- Temperature tells us how hot something is, how cold it is outside, or helps us determine if we have a fever.
- In the metric system, temperature is measured using Celsius temperature.
- On the Celsius (°C) temperature scale, water freezes at 0 °C and boils at 100 °C.
- On the Fahrenheit (°F) temperature scale, water freezes at 32 °F and boils at 212 °F.
- In the SI system, the temperature is measured using the Kelvin (K) temperature scale, on which the lowest possible temperature is 0 K.
Time
- We typically measure time in units such as years (yr), days, hours (h), minutes (min), or seconds (s).
- Of these, the SI and metric unit of time is the second (s).
- The standard now used to determine a second is an atomic clock.
2.2: Measured Numbers and Significant Figures
- Measured numbers: The numbers you obtain when you measure a quantity such as your height, weight, or temperature.
- Significant figures (SFs): All the digits including the estimated digit. Nonzero numbers are always counted as significant figures.
- Exact Numbers: Those numbers are obtained by counting items or using a definition that compares two units in the same measuring system.
- These are not measured, do not have a limited number of significant figures, and do not affect the number of significant figures in a calculated answer.
- Zeros in front of a decimal number or at the end of a nondecimal number are not significant.
2.3: Significant Figures in Calculations
Rounding Off
- If the first digit to be dropped is 4 or less, then it and all the following digits are simply dropped from the number.
- If the first digit to be dropped is 5 or greater, then the last retained digit of the number is increased by 1.
Multiplication and Division with Measured Numbers
- In multiplication or division, the final answer is written so that it has the same number of significant figures as the measurement with the fewest SFs.
Adding Significant Zeroes
- Sometimes, a calculator display gives a small whole number.
- Then we add one or more significant zeros to the calculator display to obtain the correct number of significant figures.
Addition and Subtraction with Measured Numbers
- In addition or subtraction, the final answer is written so that it has the same number of decimal places as the measurement having the fewest decimal places.
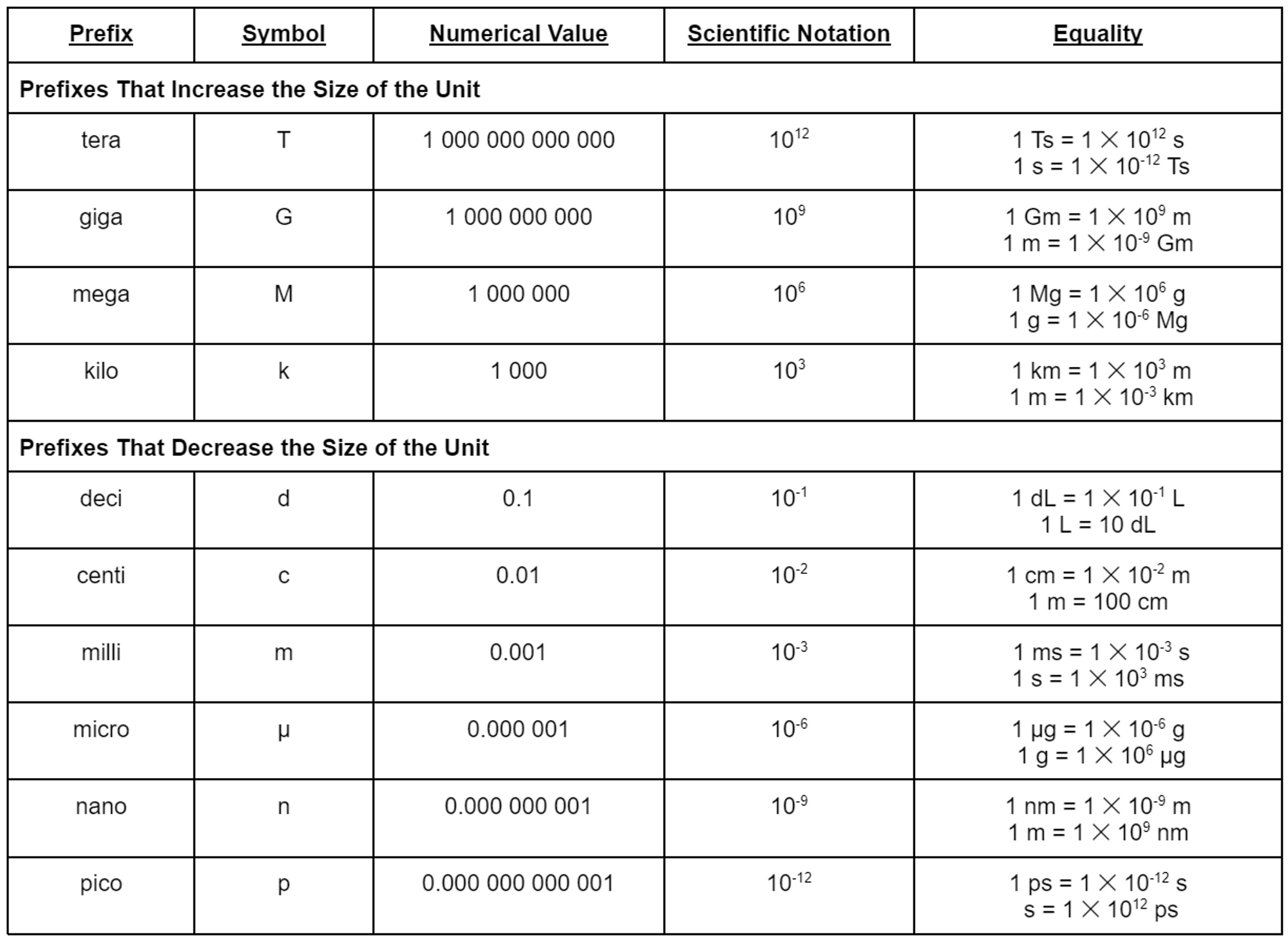
2.4: Prefixes and Equalities
- The special feature of the SI as well as the metric system is that a prefix can be placed in front of any unit to increase or decrease its size by some factor of 10.
- Prefixes such as centi, milli, and micro provide smaller units; prefixes such as kilo, mega, and tera provide larger units
Metric and SI Prefixes
Measuring Length
- When the prefix centi- is used with the unit meter, it becomes centimeter, a length that is one-hundredth of a meter (0.01 m).
- When the prefix milli- is used with the unit meter, it becomes a millimeter, a length that is one-thousandth of a meter (0.001 m).
- Equalities: This shows the relationship between two units that measure the same quantity.
Measuring Volume
- When a liter is divided into 10 equal portions, each portion is a deciliter (dL).
- There are 10 dL in 1 L.
- Laboratory results for blood work are often reported in mass per deciliter.
- When a liter is divided into a thousand parts, each of the smaller volumes is called a milliliter (mL).
- Cubic centimeter: The volume of a cube whose dimensions are 1 cm on each side. It has the same volume as a milliliter, and the units are often used interchangeably.
Measuring Mass
- A kilogram is equal to 1000 g.
- One gram represents the same mass as 1000 mg, and one mg equals 1000 μg.
- When you go to the doctor for a physical examination, your mass is recorded in kilograms, whereas the results of your laboratory tests are reported in grams, milligrams, or micrograms.
2.5: Writing Conversion Factors
- Conversion Factors: Any equality that can be written as fractions; with one of the quantities in the numerator and the other quantity in the denominator.
- The numbers in any equality between two metric units or between two U.S. system units are obtained by definition.
- When equality consists of a metric unit and a U.S. unit, one of the numbers in the equality is obtained by measurement and counts toward the significant figures in the answer.
- The usefulness of conversion factors is enhanced by the fact that we can turn a conversion factor over and use its inverse.
- An equality may also be stated within a problem that applies only to that problem.
- Equalities stated within dosage problems for medications can also be written as conversion factors.
- A percentage is written as a conversion factor by choosing a unit and expressing the numerical relationship of the parts of this unit to 100 parts of the whole.
2.6: Problems Solving Using Unit Conversion
- The process of problem-solving in chemistry often requires one or more conversion factors to change a given unit to the needed unit.
- Conversion factors are useful when changing a quantity expressed in one unit to a quantity expressed in another unit.
- In the problem-solving process, a given unit is multiplied by one or more conversion factors that cancel units until the needed answer is obtained.
2.7: Density
Density: The mass and volume of any object can be measured.
If we compare the mass of the object to its volume, we obtain density.
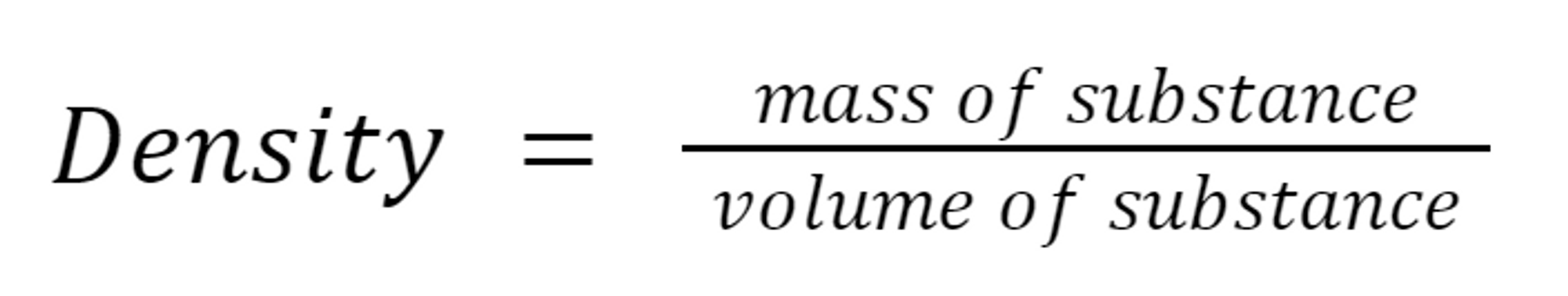
The volume of a solid can be determined by volume displacement.
- When a solid is completely submerged in water, it displaces a volume that is equal to the volume of the solid.
Density can be used as a conversion factor.
- If the volume and the density of a sample are known, the mass in grams of the sample can be calculated.
Specific Gravity: A relationship between the density of a substance and the density of water.
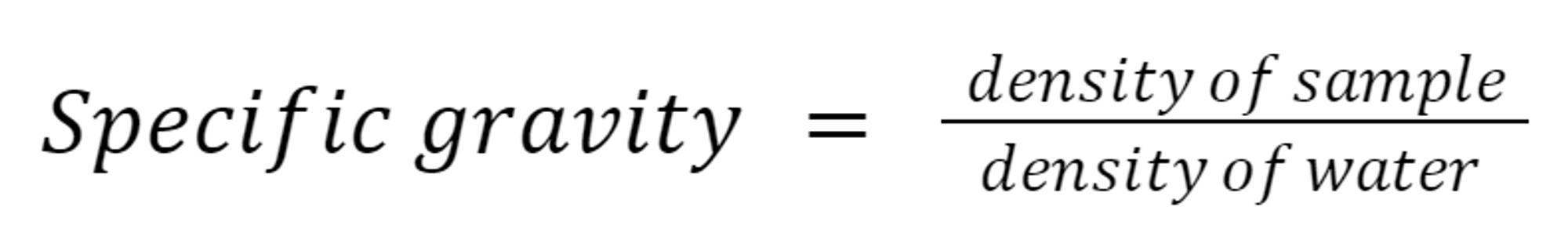
Hydrometer: An instrument often used to measure the specific gravity of fluids.
Problem Solving with Density
John took 2.0 teaspoons 1tsp2 of cough syrup for a persistent cough. If the syrup had a density of 1.20 g>mL and there is 5.0 mL in 1 tsp, what was the mass, in grams, of the cough syrup?
Step 1: State the given and needed quantities.

Step 2: Write a plan to calculate the needed quantity.

Step 3: Write the equalities and their conversion factors including density.

Step 4: Set up the problem to calculate the needed quantity.

Answer: The density of maple syrup is 1.33 g>mL. A bottle of maple syrup contains 740 mL of syrup.
Problem Solving with Specific Gravity
You have a sample of granite with density 174.8 lbs/ft3. The density of water is 62.4 lbs/ft3. What is the specific gravity of the granite now?